Оглавление
Введение 4
1 Основные теоремы о пределах 5
1.1 Вопросы для самопроверки 7
2 Производная функции 8
2.1 Вопросы для самопроверки 10
3 Приложение производной к исследованию функции
и построению ее графика 11
3.1 Вопросы для самопроверки 13
4 Неопределенный интеграл 13
4.1 Метод замены переменного 14
4.2 Интегрирование по частям 15
4.3 Интегрирование выражений, содержащих
квадратный трехчлен 17
4.4 Интегрирование рациональных дробей 20
4.5 Вопросы для самопроверки 25
5. Индивидуальные задания для контрольной работы №2 25
Библиографический список 35
Введение
Целью настоящих методических указаний является помощь студентам – заочникам в выполнении контрольной работы №2.
Работа содержит 9 заданий по различным разделам дифференциального и интегрального исчислений.
Перед выполнением контрольной работы студент должен изучить соответствующие разделы рекомендуемой литературы [1] – [3] и воспользоваться решениями типовых примеров, содержащихся в настоящих методических указаниях. Большое количество образцов решенных задач дано в руководстве к решению задач [5]. Задачи для самостоятельного решения имеются как в представленных методических указаниях, так и в сборниках задач [4], [6].
|
|
|
Номер варианта по каждому заданию студент выбирает по формуле  ,
,
где  - номер варианта
- номер варианта
 -номер задания,
-номер задания,
 -предпоследняя цифра шифра студента,
-предпоследняя цифра шифра студента,
 -последняя цифра шифра.
-последняя цифра шифра.
Пример.
Пусть шифр студента 1235, тогда:
номер варианта первого задания:  =
=  ;
;
номер варианта второго задания:  ;
;
номер варианта третьего задания:  ;
;
номер варианта четвертого задания:  ;
;
номер варианта пятого задания:  ;
;
номер варианта шестого задания:  …
…
Если получается число больше 20, то для определения варианта берут их разность. В нашем случае это будет 23-20=3. Следовательно, студент, имеющий шифр 1235, должен решать задачу №8 в первом задании, №11 – во втором, №14 – в третьем, №17 – в четвертом, №20 – в пятом, №3 – в шестом и т.д.
Основные теоремы о пределах
Пределом функции в точке «а» называется постоянная величина «b», если для любого положительного сколь угодно малого  >0 найдется такое положительное число
>0 найдется такое положительное число 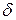 >0, что для всех
>0, что для всех  выполняется неравенство
выполняется неравенство  , что символически записывается так:
, что символически записывается так:
 ,
,
При вычислении пределов функций будем пользоваться следующими теоремами:
1. Предел алгебраической суммы функций равен алгебраической сумме их пределов.
2. Предел произведения функций равен произведению их пределов.
3. Постоянный множитель можно вынести за знак предела.
4. Предел дроби равен пределу числителя, деленному на предел знаменателя, если последний не равен нулю.
|
|
|
Кроме этих теорем широкое применение имеют два замечательных предела:
1. Предел отношения синуса бесконечно малой дуги к самой дуге равен единице.
 , или
, или  . (1.1.1)
. (1.1.1)
2. Предел выражения:
 или
или  . (1.1.2)
. (1.1.2)
Рассмотрим применение указанных теорем в решении конкретных примеров.
Пример 13.
Вычислить предел 
Решение:
а)  Подставив предельное значение аргумента в заданное выражение, получим неопределенность вида
Подставив предельное значение аргумента в заданное выражение, получим неопределенность вида  , для раскрытия которой числитель и знаменатель дроби разложим на множители, найдя предварительно корни трехчленов.
, для раскрытия которой числитель и знаменатель дроби разложим на множители, найдя предварительно корни трехчленов.

б)  Подстановка предельного значения х показывает, что имеем неопределенность вида
Подстановка предельного значения х показывает, что имеем неопределенность вида  , для раскрытия которой числитель и знаменатель дроби делим почленно на
, для раскрытия которой числитель и знаменатель дроби делим почленно на  .При этом получим пределы вида
.При этом получим пределы вида 
 и т. д., которые равны нулю.
и т. д., которые равны нулю.
 .
.
Пример 14.
Вычислить предел  .
.
Решение:
Нетрудно убедиться, что имеем неопределенность  , которая в отличие от предыдущего примера, содержит иррациональность в числителе.
, которая в отличие от предыдущего примера, содержит иррациональность в числителе.
Чтобы освободиться от этой иррациональности, умножим числитель и знаменатель дроби на выражение, сопряженное числителю. Применив затем формулу разности квадратов двух чисел и упростив числитель, можем сократить дробь.
Оставшаяся дробь не содержит нуль в знаменателе и дает возможность арифметического подсчета.

= 

=  .
.
Пример 15.
Вычислить предел  .
.
Решение:
Преобразуем данное выражение: 
В каждом сомножителе выполним несложные преобразования, позволяющие применить 1-ый замечательный предел:
 .
.
Пример 16.
Вычислить предел 
Решение:
Преобразуем исходное выражение так, чтобы использовать 2-ой замечательный предел.
Выделим внутри скобки единицу, сделаем замену переменной и преобразуем показатель степени.
 =
=  =
= 
 =
=  .
.
Вопросы для самопроверки
1. Что называется пределом функции в точке х=а?
2. Назовите основные теоремы о пределах.
3. Сформулируйте два замечательных предела.
Производная функции
Понятие производной функции является одним из основных в математике и широко применяется в различных областях науки и техники.
Производной функции y=f(x) в точке х 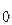 называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю произвольным образом.
называется предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю произвольным образом.
 .
.
Процедура отыскания производной называется дифференцированием функции.
Справедливы следующие правила дифференцирования:
1. (с)  =0 2. (u+v)
=0 2. (u+v)  =u
=u  +v
+v  3. (uv)
3. (uv)  =u
=u  v+uv
v+uv 
4. (сu)  = сu
= сu  5.
5. 
 .
.
На основе этого определения могут быть выведены формулы для производных основных элементарных функций:
1.  , в частности:
, в частности:  ;
;
2.  , в частности:
, в частности:  ;
;
3.  , в частности:
, в частности:  ;
;
4.  ; 5.
; 5.  ;
;
6.  ; 7.
; 7.  ;
;
8.  ; 9.
; 9.  ;
;
10.  ; 11.
; 11.  .
.
Особый интерес представляет производная сложной функции.
Если у=f(u), где u=  , тогда у
, тогда у  .
.
Пример 1 Найти производную функции:  .
.
Решение.
Используя правило дифференцирования сложной функции, а также формулу нахождения производной степенной функции, получим:
 .
.
Пример 2 Найти производную функции  .
.
Решение.
Воспользуемся правилом дифференцирования произведения двух функций и формулами нахождения производной от показательной и логарифмической функции.
 = =
= =  = =
= = 
=  .
.
Пример 3 Найти производную функции:  .
.
Используем правило дифференцирования дроби и формулы нахождения производной от  и степенной функции.
и степенной функции.
 =
=

Пример 4 Найти производную функции:  .
.
Решение.
При нахождении производной неявно заданной функции продифференцируем обе части уравнения по переменной 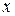 , имея в виду, что
, имея в виду, что 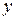 есть функция от
есть функция от 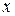 и выразим
и выразим  из полученного линейного относительно
из полученного линейного относительно  уравнения.
уравнения.


Если функция задана параметрическими уравнениями, то ее производная по переменной 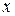 находится по формуле
находится по формуле  .
.
Пример 5 Найти производную функции: 
Решение.
Поскольку  ,
,  , то
, то
 .
.
Пример 6 Найти производную функции:  .
.
Решение.
Применим метод логарифмического дифференцирования, для чего логарифмируем заданное выражение по основанию « », потом дифференцируем и находим у
», потом дифференцируем и находим у  .
.
|
|
|
 .
.
Дифференцируем:
 =
=
= 
Находим из полученного уравнения у  :
:
 .
.
Вопросы для самопроверки
1. Что называется производной функции?
2. Каковы правила нахождения производных от суммы, произведения, дроби, от постоянной величины?
3. Как найти производную сложной функции?
4. Правило дифференцирования функции, заданной неявно.
5. В чем заключается метод логарифмического дифференцирования?
Приложение производной к исследованию функции
 2015-10-22
2015-10-22 1787
1787








