Гарантирующая стратегия управления при однопараметрической коррекции летательного аппарата

Обратимся снова в задаче однопараметрической коррек­ции ЛА, принимая в качестве математической модели скалярное уравнение

где, как и прежде, 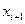— промах, который будет иметь место после проведения i -го корректирующего (управляющего) воздействия — частная производная конечного промаха по управлению в i –ый момент времени, — ошибка реализации корректирующего воздействия. Однако в отличие от стохастического подхода теперь будем считать, что никакой статистической информации об этом возмущении нет. Известен лишь диапазон изменения возмущения , задаваемый неравенством

где — заданная предельная величина возмущения.

Поставим задачу определения последовательности таких управ­ляющих воздействий , которые гарантируют достижение требуемой конечной точности, т. е. выполнение условия

здесь — максимально допустимая величина конечного промаха при минимальных затратах топлива, оцениваемых величиной

Гарантированное выполнение условия может быть предcтавлено в виде

Здесь операцию max предполагается осуществлять по всем допус­тимым возмущениям , через M обозначено допустимое множество возмущений .

Для решения задачи составим, обобщенный критерий оптималь­ности

где — множитель Лагранжа. Можно показать, что исходная задача по минимизации критерия J ° с учетом ограничения может быть решена путем решения задачи минимизации обобщен­ного критерия J при фиксированном с последующим выбором а из условия . Действительно, если через обозначить стра­тегию управления, доставляющую минимум критерию J (и, ) при фиксированном , то по определению будем иметь, что для любых управлений и

или

Отсюда следует, что при условии

Поэтому если подобрать такое, что

то управление обеспечит минимум критерию при усло­вии .

Для отыскания оптимальной стратегии управления обратимся к рекуррентному соотношению (6.26), которое в данном случае принимает вид

с граничным условием

Рассмотрим момент проведения последней коррекции. Для i—N будем иметь

где

Таким образом, для определения оптимального управления необходимо найти функцию максимума . Рас­крывая операцию максимума в выражении для , получаем инте­ресующую нас зависимость

Заметим, что минимум функции достигается в точке

и значение функции максимума при этом равно

Если бы рассматривалась задача управления только конечным состоянием с минимизацией функции максимума , то найденное управление было бы искомым оптимальным. В данном же случае оптимальное управление определится из условия (6.27). Нетрудно убедиться, например графически, что это управление зависит от множителя а и равно

Здесь через обозначено «особое» управление, которое может принимать любое значение из диапазона . Оценка конечной точности, определяемой функцией максимума при стратегии управления (6.28), имеет вид

С учетом найденного алгоритма управления получаем следующее выражение для функции будущих потерь:

Если теперь допустить, что рассматривается проведение всего од­ной коррекции (N=l), то в зависимости от значения могут иметь место три случая.

Случай 1, когда , интереса не представляет, так как требуемая конечная точность при этом достигнута и коррекции проводить вообще не требуется.

Случай 2, когда выполняется неравенство , соответствует «особому» управлению и является основным рас­четным случаем при N=1. Так как при этом должно выполняться равенство

то искомое управление

где

Функция будущих потерь при этом равна

Случай З, когда означает, что требуемая точность не может быть достигнута при проведении одной коррекции и необхо­димо проведение дополнительных коррекций.

Объединяя полученные результаты, можно окончательно за­писать для алгоритма оптимального управления

для функции будущих потерь

и для оценки конечной точности

Если одноимпульсная коррекция не обеспечивает достижения тре­буемой конечной точности и имеет место равенство

то необходимо рассмотреть случай проведения двух коррекций. Повторяя ранее изложенные рассуждения для i=N, можно полу­чить аналогичные результаты и для момента i=N —1.

Применяя эту процедуру последовательно для моментов време­ни N, N —1,..., i —1, i и считая при этом, что проведение рассматри­ваемого на каждом шаге числа коррекции не гарантирует достиже­ния требуемой точности, получим алгоритм управления на t-м шаге в виде

где

Оценка конечной точности при этом будет иметь вид

И, наконец, функция будущих потерь равна

причем параметр удовлетворяет следующему рекуррентному со­отношению

при граничном условии .