Модуль 4 «методы оптимизации»

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 10

Методы оптимизации

Главной задачей и конечной целью решения большого числа разнообразных исследовательских проблем управления, проектирования и планирования обычно является достижение и поддержание экстремальных, то есть наилучших, показателей. Процесс нахождения и поддержания наилучших (в определенном смысле) значений целевой функции объекта называется оптимизацией.

Критерий оптимизации (целевая функция) Y обычно задается, иногда исследователь задает ее сам. Этот критерий должен удовлетворять следующим основным условиям:

– нести в себе существенную информацию об объекте, о качестве процесса;

– измеряться с достаточной точностью;

– носить обобщенный характер, то есть отражать свойства и качества процесса в целом.

Если математическое ожидание критерия оптимизации у есть функция от вектора входных управляемых переменных (факторов), то есть

 

M{y} = f(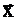) = f(x₁, x₂, …, x_k), (10.1)

 

где k – число факторов,

то задача оптимизации сводится к отысканию таких значений факторов

 

* = (x₁*, x₂*, …, x_k*), (10.2)

 

при которых целевая функция достигает экстремума (максимума или минимума).

Если на объект воздействуют аддитивные помехи, то зависимость (10.1) выражает не функциональную, а регрессионную зависимость, которая в (k+1)-мерном пространстве n факторов x_i (i =1, 2, …, k) и целевой функции y образует поверхность отклика.

Для решения задачи оптимизации, то есть отыскания вектора (10.2), можно применить два принципиально разных подхода:

1 – если известна или есть возможность найти n-факторную математическую модель для той части пространства, где расположен экстремум функции отклика, то задачу оптимизации решают аналитическим или численным методом;

2 – если математическое описание не получено по каким-либо причинам, то осуществляют экспериментальный поиск области оптимума.

В первом случае используют известное из математического анализа свойство функций, имеющих экстремум: в точке экстремума (максимума или минимума) первая производная этой функции обращается в нуль. Если необходимо найти полную производную в n-факторном пространстве, то находят n частных производных по каждому из n факторов и получают систему из n уравнений

∂y/∂x₁ = 0;

∂y/∂x₂ = 0;

………….. (10.3)

∂y/∂x_k-1 = 0;

∂y/∂x_k = 0

 

Решением системы (10.3) и является вектор (10.2). Однако во многих практических случаях аналитическая зависимость (10.1) неизвестна или ее нахождение представляет собой сложную задачу.

Тогда, если имеется возможность одновременно наблюдать все n факторов и целевую функцию, задачу оптимизации проще решить с помощью второго подхода, то есть с помощью экспериментального поиска. Для этого сначала осуществляют изучение характера поверхности отклика в районе первоначально выбранной точки факторного пространства (с помощью специально спланированных «пробных» опытов). Затем совершают «рабочее» движение в сторону экстремума, причем направление движения определяют по результатам пробных опытов. Такое движение может осуществляться путем ряда этапов, которые могут объединяться в «циклы».

После выхода в район экстремума оптимальную точку можно уточнить одним из двух способов:

– постановкой дополнительных, особым образом спланированных, опытов;

– получением математической модели второго или более высокого порядка и последующим решением системы уравнений (6.3).

Задача надежного отыскания экстремума усложняется, если на объект воздействуют случайные помехи. Тогда каждое измеренное (наблюдавшееся) значение целевой функции оказывается суммой истинного ее значения и случайной помехи. Для повышения надежности результатов применяют специальные методы, например в каждой запланированной точке факторного пространства выполняют несколько параллельных опытов.

Если характеристики объекта изменяются, смещаются во времени (дрейф), то это создает дополнительные трудности и приходится создавать специальные планы эксперимента.

 

Метод Гаусса-Зайделя

 

Метод Гаусса-Зайделя предусматривает поочередное нахождение частных экстремумов целевой функции по каждому фактору x_i (i =1, 2, …, n). При этом на каждом i-м этапе стабилизируют n-1 факторов и варьируют только один, i-й фактор. Задачу поиска экстремума решают в несколько этапов, которые затем объединяют в циклы.

Рассмотрим последовательность поиска максимума методом Гаусса-Зайделя с иллюстрацией двухфакторного примера. Графическая интерпретация метода дана на рисунке 10.1, где на плоскости двух факторов x1, x2 изображена функция отклика у топографическим способом с помощью замкнутых линий постоянного уровня этой оптимизируемой выходной функции. Эти линии соответствуют некоторым относительным величинам, однако форма функции отклика до начала исследования обычно неизвестна.

I этап. Производится поиск частного экстремума по первому фактору x₁, остальные факторы остаются неизменными, то есть стабилизируются.

1 – Выбирают основную (начальную, базовую) точку М₀, обычно она соответствует номинальному режиму ведения технологического процесса 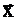₀=(x₁₀; x₂₀; …; x_k0). Иногда эту точку выбирают в центре области, которую желательно исследовать, либо в центре области ограничений, если они имеются.

 

x ₂

 

M₁₁ M₉ M₁₂ M₁₃ M₁₄

 

M₈ M₁₅

Δx₂ M₆ M₅ M₄ M₃ M₂ M₀ M₁

x₂₀

M₇

x ₁

0 x₁₀

Δx₁

 

Рисунок 10.1 – Поиск экстремума функции отклика

методом Гаусса-Зайделя

 

2 – Выбирают интервал варьирования Δx₁ по фактору x₁. Интервал не должен быть слишком малым, иначе движение к экстремуму окажется замедленным. Кроме того, на интервале варьирования Δx_i (i=1, 2, …, k) изменение целевой функции Δy должно быть существенно большим, чем погрешность ее измерения δy (не менее чем в 5–10 раз)

3. Определяют координаты пробных точек М₁ и М₂:

(М₁) = (x₁₀+Δx₁; x₂₀; …; x_k0),

(М₂) = (x₁₀–Δx₁; x₂₀; …; x_k0).

4. В точках М₁ и М₂ ставят пробные опыты (для повышения точности результатов могут выполняться параллельные опыты) и измеряют отклики у(М₁) и у(М₂).

5. Сравнивают полученные отклики, и если у(М₂) > у(М₁), то совершают рабочее движение на один рабочий шаг Δx₁ по направлению в точку М₃.

6. Аналогичные шаги продолжают в том же направлении до тех пор, пока на каком-то m-м шаге не окажется, что у(М_m) < у(М_m–1), то есть значение отклика в очередной, m-й рабочей точке станет уменьшаться, – это и служит признаком достижения частного экстремума. За частный экстремум принимают (m–1)-ю точку с откликом у(М_m–1). На рисунке 4.1 это точка М₅.

II этап. Его проводят в том порядке, что и I этап, с той лишь разницей, что стабилизируют все факторы, кроме x₂. За новую базовую точку принимают точку с координатами

(М_m–1) = (x₁₀+Δx₁·(m–2); x₂₀; …; x_k0),

а x₂ варьирую на выбранную по аналогичным условиям величину интервала Δx₂. По достижении частного экстремума по фактору x₂ точку нового частного экстремума принимают за новую базовую точку. На рисунке 10.1 это точка М₉.

Первый цикл продвижения к экстремуму заканчивается n-м этапом, на котором стабилизируются все факторы, кроме x_k. Для него выбирают интервал варьирования Δx_k и совершают пробное, а затем рабочее движение до достижения частного экстремума по фактору x_k. Если экстремум не достигнут, то выполняют второй цикл поиска.

Второй цикл, как и первый, начинается с I этапа, на котором варьируют фактор x₁ (i ≠ 1), затем последовательно выполняют k этапов по каждому из k факторов.

Поисковое шаговое движение к экстремуму заканчивают по достижении такой точки факторного пространства, при движении из которой в любую сторону по всем n факторным осям x_i в положительном или отрицательном направлениях значения отклика оказываются меньшими. Такую точку принимают за экстремум (в рассматриваемом случае – максимум).

Достоинства метода Гаусса-Зайделя:

– простота стратегии и наглядность;

– высокая помехозащищенность в смысле выбора направления движения.

Недостатки:

– путь к главному экстремуму оказывается обычно долгим, особенно при большом числе факторов;

– если поверхность отклика имеет сложную форму, то использование метода может привести к ложному ответу на вопрос о месте расположения экстремума;

– метод не дает информации о взаимодействиях факторов.

Исторически метод Гаусса-Зайделя известен как первый из рассматриваемых. При увеличении количества воздействующих факторов до 5–6 применять этот метод для оптимизации процессов неэффективно.