Непрерывно-стохастические модели 8 страница

Дисперсионный анализ греко-латинского квадрата проводится так же, как и анализ обычного латинского квадрата, с учетом четвертого фак­тора D (греческая буква). Сумма квадратов для греческой буквы имеет число степеней свободы 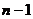. Число степеней свободы остаточной сум­мы, определяемой, как и ранее, в виде разности между общей суммой квадратов и суммами квадратов всех факторов, равна . Если наложить друг на друга три ортогональных латинских квадрата, получим латинский квадрат третьего порядка, n ортогональных квадратов — латинский квадрат n -го порядка. Полученные квадраты называют также гипер-греко-латинскими квадратами.

При n уровнях в план можно ввести фактор. Число степеней свободы остаточной суммы при этом будет равно нулю. Такие планы называются насыщенными. Построим насыщенный план для . Нало­жим для этого друг на друга четыре полученных ортогональных латин­ских квадрата 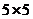[см. (III.105) —(III.108)], составляющих полный ряд ортогональных латинских квадратов 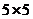(табл. 18). Исходный латинский квадрат (III.105) соответствует уровням фактора С, второй квадрат (III.106) —уровням фактора D и т. д. Уровни факторов обозначены цифра­ми. Соответствующий план эксперимента для шести факторов приведен в табл. 19.

Полученный план является насыщенным, так как число степеней свободы остаточной суммы, определяемое по формуле , где k — число изучаемых факторов, равно нулю.

План представляет собой реплику от ПФЭ . Такие планы обычно применяют на первых стадиях исследования процесса, когда приходится

 

Таблица 19. План эксперимента ,

Номер опыта	A	B	C	D	y	Номер опыта	A	B	C	D	y

 

проводить сложный перебор каче­ственных факторов с тем, чтобы выделить перспективные комбинации для дальнейше­го исследования и отсеять неприемлемые. Использование греко-латинских и гипер-греко-латинских квадратов в качестве пла­нов эксперимента одновременно дает эконо­мию в числе наблюдений и приводит к упрощению вычислений.

Основным допущением, лежащим в ос­нове применения греко-латинского квадрата и квадратов высших порядков, является пред­положение об отсутствии взаимодействий между факторами. Проверить адекватность принятой линейной модели, как и при применении латинских квадратов, можно только при наличии параллельных опытов.

5. Латинские кубы. Полному факторному эксперименту для трех фак­торов соответствует кубическое расположение из n элементов, включающее позиций. Трем ребрам куба соответствуют факторы А, В и С с уровнями 0, 1, 2, …, n - 1 (рис. 22). Если ввести в план четвертый фактор D и уровни этого фактора (0, 1, 2,..., n - 1) разместить в соответствующих опытам точках кубического расположения, то полу­чится латинский куб размера n первого порядка.

Латинским кубом размера n первого порядка называют кубическую таблицу из n элементов, расположенных в позициях, в которую каждый элемент входит 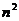раз и встречается в каждой из плоскостей, парал­лельных координатным плоскостям , , , одинаковое для всех элементов и равное n число раз. Действительно, уровни дополни­тельного фактора D (элементы латинского куба) встречаются в плане одинаковое и равное 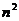число раз и встречаются в каждой из коорди­натных плоскостей (т. е. с уровнями трех факторов А, В, С)одинаковое и равное n число раз (табл. 20).

 

Таблица 20. латинский куб первого порядка

C =0

A

B

C =1

A

B

C =2

A

B

 

Соответствующая матрица планирования для латинского куба с раз­мерами , приведена в табл. 21.

Планирование эксперимента по латинскому кубу первого порядка позволяет включить в рассмотрение четыре фактора (А, В, С и D).Отли­чие от греко-латинского квадрата, который тоже дает возможность изучать влияние

 

Таблица 21. План эксперимента ,

Номер опыта	A	B	C	D	y	Номер опыта	A	B	C	D	y

 

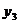
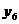
четырех факторов, состоит в том, что в латинском кубе три фактора (А, В и C) считаются главными и один фактор (D)составляет элиминирующую группировку, а в греко-латинском квадрате главными считаются два фактора А и В, а С и D составляют двойную элиминирую­щую группировку. Число опытов в кубе в n раз больше, чем в греко-латинском квадрате. Латинский куб без повторных опытов применяется в предположении линейной модели процесса:

(III.108)

где — общее среднее; — эффект фактора А на i -м уровне, i = 0, 1, 2,..., n -1; — эффект фактора В на j -муровне, j = 0, 1, 2,..., n - 1; — эффект фактора D на q -муровне, q = 0, 1, 2,..., n - 1; — эффект фак­тора D на l -м уровне; — случайная ошибка эксперимента.

Статистический анализ латинского куба первого порядка без повтор­ных опытов удобно проводить по следующему алгоритму. Определяют: 1) итоги для всех факторов на каждом уровне:

Применительно, например, к плану, приведенному в табл. 21, имеем

2) сумму квадратов всех наблюдений

(III.109)

3) сумму квадратов итогов по фактору A, деленную на ,

(III.110)

4) сумму квадратов итогов по фактору В,деленную на ,

(III.111)

5) сумму квадратов итогов по фактору С, деленную на ,

(III.112)

6) сумму квадратов итогов по фактору D, деленную на ,

(III.113)

7) корректирующий член, равный квадрату общего итога, деленному на число всех наблюдений,

(III.114)

8) общую сумму квадратов, равную разнице между суммой квадратов всех наблюдений и корректирующим членом,

(III.115)

9) сумму квадратов, обусловленную фактором A,

(III.116)

10) сумму квадратов, обусловленную фактором В,

(III.117)

11) сумму квадратов, обусловленную фактором С,

(III.118)

12) сумму квадратов, обусловленную фактором D,

(III.119)

13) остаточную сумму квадратов

(III.120)

Результаты расчета представляют в виде таблицы дисперсионного анализа (табл. 22).

 

Таблица 22. Дисперсионныйанализ для латинского куба