|
 ,
,
коэффициенты которого  и
и  непрерывны.
непрерывны.
Пусть
 и
и 
– частные решения уравнения (4.3.13), то есть решения, не содержащие произвольных постоянных.
|
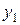 и
и 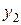 называются линейно зависимыми, если можно подобрать постоянные числа
называются линейно зависимыми, если можно подобрать постоянные числа  и
и  , не равные одновременно нулю такие, что линейная комбинация этих функций тождественно равна нулю, то есть
, не равные одновременно нулю такие, что линейная комбинация этих функций тождественно равна нулю, то есть
 .
.
В противном случае, если таких чисел подобрать нельзя, решения 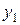 и
и 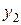 называются линейно независимыми. Иными словами, если функции
называются линейно независимыми. Иными словами, если функции 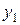 и
и 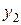 линейно независимы и имеет место тождество (4.3.14), то
линейно независимы и имеет место тождество (4.3.14), то  .
.
Очевидно, решения 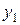 и
и 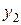 будут линейно зависимы тогда и только тогда, когда они пропорциональны друг другу, т.е. если
будут линейно зависимы тогда и только тогда, когда они пропорциональны друг другу, т.е. если
|

(или наоборот  ), где постоянная а – коэффициент пропорциональности.
), где постоянная а – коэффициент пропорциональности.
Зная два линейно независимых решения 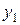 и
и 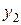 уравнения (4.3.13), легко получить общее решение этого уравнения. А именно, имеет место теорема.
уравнения (4.3.13), легко получить общее решение этого уравнения. А именно, имеет место теорема.
|
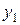 и
и 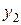 - линейно независимые частные решения линейного однородного уравнения второго порядка (4.3.13), то общее решение уравнения есть линейная комбинация этих частных решений, т.е. общее решение уравнения (4.3.13) имеет вид
- линейно независимые частные решения линейного однородного уравнения второго порядка (4.3.13), то общее решение уравнения есть линейная комбинация этих частных решений, т.е. общее решение уравнения (4.3.13) имеет вид|
|
|
 ,
,
где  и
и  – произвольные постоянные (
– произвольные постоянные ( ,
,  ).
).
Итак, чтобы найти общее решение уравнения (4.3.13), достаточно знать два его частных линейно независимых решения 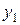 и
и 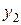 .
.
 2017-10-31
2017-10-31 491
491








