Определение доказуемой (выводимой) формулы

Этапом в построении исчисления высказываний является выделение класса доказуемых (выводимых) формул.

Сначала определяются исходные доказуемые выводимые формулы (аксиомы), а затем определяются правила вывода, которые позволяют из имеющихся доказуемых формул получить новые доказуемые формулы.

 

 

2.9 Аксиоматический метод

 

Ø Определение Аксиоматический метод - способ построения научной теории, при котором в её основу кладутся некоторые исходные положения (суждения) — аксиомы, из которых все остальные утверждения этой науки должны выводиться чисто логическим путём, посредством доказательств.

Назначение аксиоматического метода состоит в ограничении произвола при принятии научных суждений в качестве истин данной теории. Построение науки на основе аксиоматического метода обычно называется дедуктивным.

Все понятия дедуктивной теории вводятся посредством определений, выражающих их через ранее введённые понятия. В той или иной мере дедуктивные доказательства, характерные для аксиоматического метода, применяются во многих науках. Главной областью его приложения до сих пор остаются математика и символическая логика, а также некоторые разделы физики (механика, термодинамика, электродинамика и др.).

Аксиоматический метод прошёл в своём историческом развитии 3 стадии.

Первая связана с построением геометрии в Древней Греции. Основное сочинение этого периода — «Начала» Евклида (хотя, по-видимому, и до него Пифагор, которому приписывается открытие аксиоматического метода, а затем Платон и его ученики немало сделали для развития геометрии на основе аксиоматического метода).

В то время считалось, что в качестве аксиом должны выбираться суждения, истинность которых «самоочевидна», так что истинность теорем считалась гарантированной безупречностью самой логики. Но Евклиду не удалось ограничиться чисто логическими средствами при построении геометрии на основе аксиом. Он охотно прибегал к интуиции в вопросах, касающихся непрерывности, взаимного расположения и равенства геометрических объектов. Впрочем, во времена Евклида такие обращения к интуиции могли и не восприниматься как выход за пределы логики — прежде всего потому, что сама логика не была ещё аксиоматизирована. Не было и достаточной отчётливости во введении первоначальных понятий и при определении новых понятий.

Начало второй стадии в истории аксиоматического метода связывают обычно с открытием Н. И. Лобачевским, Я. Больяй и К. Ф. Гауссом возможности построить непротиворечивым образом геометрию, исходя из систем аксиом, отличной от евклидовой. Это открытие разрушило убеждение в абсолютной («очевидной» или «априорной») истинности аксиом и основанных на них научных теорий. Теперь аксиомы стали пониматься просто как исходные положения данной теории, вопрос же об их истинности в том или ином смысле (и выбор в качестве аксиом) выходит за рамки аксиоматической теории как таковой и относится к её взаимоотношению с фактами, лежащими вне её. Появилось много (и притом различных) геометрических, арифметических и алгебраических теорий, которые строились средствами аксиоматического метода (работы Р. Дедекинда, Г. Грасмана и др.). Эта стадия развития аксиоматического метода завершилась созданием аксиоматических систем арифметики (Дж. Пеано, 1891), геометрии (Д. Гильберт, 1899), исчисления высказываний и предикатов (А. Н. Уайтхед и Б. Рассел, Англия, 1910) и аксиоматической теории множеств (Э. Цермело, 1908).

Гильбертовская аксиоматизация геометрии позволила Ф. Клейну и А. Пуанкаре доказать непротиворечивость геометрии Лобачевского относительно евклидовой геометрии посредством указания интерпретации понятий и предложений неевклидовой геометрии в терминах геометрии Евклида, или, как говорят, построения модели первой средствами второй. Метод моделей (интерпретаций) стал с тех пор важнейшим методом установления относительной непротиворечивости аксиоматических теорий. В то же время со всей отчётливостью выявилось, что, кроме «естественной» интерпретации (т. е. той, ради уточнения и развития которой данная теория строилась), у аксиоматической теории могут быть и др. интерпретации, причём её можно с равным основанием считать «говорящей» о каждой из них.

Последовательное развитие этой идеи и стремление точно описать логические средства вывода теорем из аксиом привели Гильберта к концепции формального аксиоматического метода, характерной для третьей, современной его стадии.

Основная идея Гильберта — полная формализация языка науки, при которой её суждения рассматриваются просто как последовательности знаков (формулы), не имеющие как таковые никакого смысла (который они приобретают лишь при некоторой конкретной интерпретации). Это относится и к аксиомам — как общелогическим, так и специфическим для данной теории. Для вывода теорем из аксиом (и вообще одних формул из других) формулируются специальные правила вывода (например, т. н. правило modus ponens — «правило зачёркивания», позволяющее получить В из А и «А влечёт В»). Доказательство в такой теории (исчислении, или формальной системе) — это просто последовательность формул, каждая из которых либо есть аксиома, либо получается из предыдущих формул последовательности по какому-либо правилу вывода. По замыслу Гильберта, в рамках созданной им теории доказательств, можно было бы доказать непротиворечивость и полноту всей классической математики (т. е. доказуемость каждой формулы, истинной при некоторой определённой интерпретации). Несмотря на ряд значительных результатов в этом направлении, гильбертовская программа в целом (её обычно называют формализмом) невыполнима, т. к., согласно важнейшему результату К. Гёделя (1931), всякая достаточно богатая непротиворечивая формальная система непременно неполна (т. н. теорема о неполноте). Оказывается, в сколько-нибудь сложной аксиоматической системе (посложнее, чем кубики, но достаточно даже арифметики) существуют формулы, которые нельзя ни доказать, ни опровергнуть.Может в этом причина, что не все школьные задачки имеют решения?!

'''Теорема Гёделя о неполноте''' гласит, что любая непротиворечивая формальная теория, включающая арифметику целых чисел, неполна.

Каким же образом доказывается теорема Геделя о неполноте формальных систем? Идея доказательства заключается в том, чтобы построить пример формулы, которая была бы недоказуема и, вместе с тем, содержательно истинна. Таковой являлась бы формула, содержательный смысл которой заключается в том, что она утверждает свою собственную недоказуемость, т.е. невыводимость из аксиом рассматриваемой формальной системы.

Теорема Гёделя свидетельствует об ограниченности аксиоматического метода (хотя определённые расширения допускаемых метатеоретических средств и позволили немецкому математику Г. Генцену, П. С. Новикову и др. математикам получить доказательство непротиворечивости формализованной арифметики).

Аксиоматический метод подвержен также критике, исходящей из различных семантических (см. Логическая семантика) критериев. Так, интуиционисты (Л. Э. Я. Брауэр, Г. Вейль и др.) не признают обоснованности в применении к бесконечным множествам принципа исключенного третьего (см. Исключённого третьего принцип) между тем этот принцип не только берётся в качестве логической аксиомы в большинстве формальных теорий, но и используется по существу (хотя и неявно) в основных предпосылках гильбертовской программы, согласно которой непротиворечивость теории — достаточное условие её «истинности».

Пример Существование Бога недоказуемо! Иначе это была бы теорема.Это только кажется, что аксиоматические системы - это сложно. Любой может напридумывать их сколько угодно. Более простым делом вам вряд ли приходилось заниматься. Пример В качестве языка можно объявить любые "слова" из последовательности буквы Я. Букву Я объявим аксиомой. Правило вывода будет удваивать букву Я.То есть придумана теория, в которой выводимы любые последовательности (слова), состоящие из буквы Я.Я ЯЯ ЯЯЯ... ЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯЯ...

И все бы хорошо, только такая строго заданная теория мало что дает создателю, кроме радости созидания. Теория, созданная из буквы Я, не привязана к понятию истинности. Поэтому она бессмысленна, как бессистемная перестановка детских кубиков.

 

2.10 Система аксиом исчисления высказываний (ИВ)

 

На сегодняшнее время известно»20 ИВ, которые отличаются друг от друга аксиомами (схемами аксиом) и правилами выводов.

Пример ИВ Уйтхеда и Рассела (1920¸1930, Англия).

Аксиомы

А 1. (А Ú А) ® А – закон тавтологии

А 2. А ® (В Ú А) – закон добавления

А 3. (А Ú В)®(В Ú А) – закон перестановки

А 4. (А Ú В)®((С Ú А) ® (С Ú В)) – закон суммирования

Правила вывода

Р1: Подстановка А вместо В;

Р2: Замена на эквивалентную формулу

Р3: Modus ponens ⊦ В.

Система аксиом современной исчисления высказываний состоит из 11 аксиом (по сути представляющих собой тождественно истинные формулы алгебры логики- тавтологии), которые делятся на четыре группы.

Первая группа аксиом (содержащая только импликацию).

: .

: .

Вторая группа аксиом (к импликации присоединилась конъюнкция):

:

: .

: .

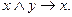
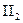Третья группа аксиом (к импликации присоединилась дизъюнкция):

:

:

: .

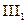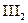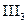Четвертая группа аксиом (к импликации присоединилось отрицание):

:

:

:

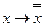
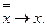
Таким образом, множество аксиом исчисления высказываний, заданное 4 группами аксиом, бесконечно.

Если помнить, что одной из интерпретаций исчисления высказываний является алгебра высказываний, то легко видеть, что в данной интерпретации перечисленные выше аксиомы (как и вообще доказуемые формулы) являются тавтологиями в алгебре высказываний.

 

2.11 Правила вывода

 

Основных правил вывода в исчислении высказываний два: правило подстановки и правило простого заключения.