2017-11-01
237
ШАРООБРАЗНОЙ ЧАСТИЦЫ, ДВИЖУЩЕЙСЯ В
НЕПОДВИЖНОЙ ВОЗДУШНОЙ СРЕДЕ
Целью работы является пошаговое решение дифференциальных уравнений падения частиц шарообразной формы с наклонной полки в неподвижной среде с подбором числа Re, определение диаметра частицы и сравнение его значения с заданным.
Основы теории
Во многих отраслях промышленности, связанных с переработкой сыпучих материалов, необходимо обеспечить получение продуктов с определенным гранулометрическим составом. Гранулометрический состав продуктов обычно регламентируется ГОСТ и ТУ, причем, чем в высокотехнологичных процессах требования к гранулометрическому составу продуктов возрастают. Для фракционирования материалов в различных отраслях промышленности применяются разнообразные аппараты, в которых осуществляются разные способы классификации. Наиболее универсальным и эффективным способом является воздушная классификация.
Создание аппарата для разделения частиц должно осуществляться на основе теоретических и экспериментальных исследований процесса разделения.
|
|
|
При моделировании необходимо учесть влияние параметров единичной частицы на результаты разделения смеси в аппарате и количественно оценить действие сил на отдельную частицу.
В данной лабораторной работе рассмотрено исследование закономерностей движения частиц по наклонной полке классификатора и частный случай схода с нее в неподвижную воздушную среду.
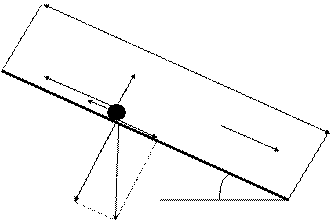
Движение частицы по плоскости определяется взаимодействием следующих сил (рис. 4.1):
 |
L
F тр F c
N
P sin a V
P сos a P a
Рис. 4.1. Схема сил, действующих на частицу,
движущуюся по наклонной плоскости
· гравитационной силы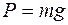 
, (4.1)
где m - масса частицы, кг;
g - ускорение свободного падения; м/с2;
· силы трения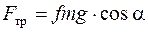 
, (4.2)
где f – обобщенный коэффициент трения;
a - угол наклона плоскости к горизонту;
· силы сопротивления движению частицы со стороны среды
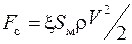, (4.3)
где x - коэффициент аэродинамического сопротивления среды, зависящий от числа Рейнольдса,
V - скорость частицы относительно среды, м/с;
S м - аэродинамическое сечение частицы, м.
Уравнение движения частицы по плоскости
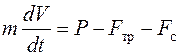. (4.4)
Так как сила аэродинамического сопротивления примерно на два порядка меньше силы тяжести и силы, примем F c = 0.
Тогда
;
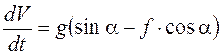. (4.5)
Для шарообразной частицы
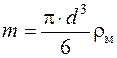, (4.6)
где rм - плотность материала частицы.
Интегрирование уравнения (4.5) дает
;
.
При t = 0, V = 0 C 0 = 0 получим
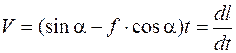. (4.7)
Далее 
; 
.
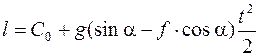При t = 0, l = 0, C 0 = 0
;
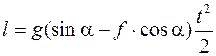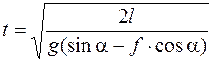. (4.8)
На основе многочисленных экспериментальных исследований, значение обобщенного коэффициента трения определим как
|
|
|
. (4.9)
Рассмотрим движение частицы при сходе с наклонной плоскости (рис. 4.2).
 |
a
F c F c sin a
W R y x
F c сos a P ma
U
y
Рис. 4.2. Схема сил, действующих на частицу
На частицу действуют:
· сила тяжести P;
· подъемная сила Архимеда R y
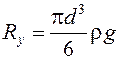; (4.10)
· cила аэродинамического сопротивления F c
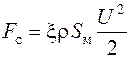; (4.11)
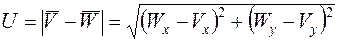, (4.12)
где Wx, Wy - проекции вектора скоростного потока на координатные оси,
Vx, Vy - проекции вектора скорости частицы на координатные оси.
В неподвижной среде Wx = Wy = 0, а уравнение (4.12) будет выглядеть
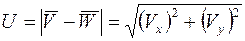, (4.13)
при этом проекции Ux = Vx, Uy = Vy.
Так как при движении частицы в воздухе r << rм, силой Ry можно пренебречь.
Проекции силы аэродинамического сопротивления на координатные оси можно представить как
(4.14)
или
. (4.15)
Система уравнений движения частицы запишется
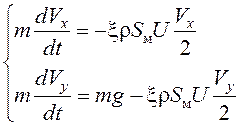(4.16)
Коэффициент аэродинамического сопротивления рассчитывался по формуле Адамова Г.А., имеющей сравнительно небольшую погрешность в широком диапазоне чисел Re
.
Число Рейнольдса соответственно
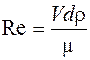, (4.17)
где m - динамический коэффициент вязкости среды, Па×с;
d - диаметр частицы, м.
После подстановки
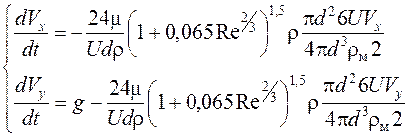
или
, (4.18)
где t - время релаксации
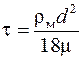; (4.19)
. (4.20)
Примем
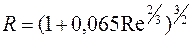. (4.21)
Решая уравнение (4.18) для проекций на ось x, получим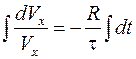 
.
Соответственно
; 
,
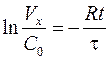где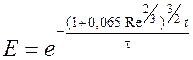 
или 
. (4.22)
При t = 0, V x = V x0, C 0 = V x0
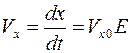(4.23)
Решая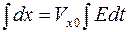 
, получим 
.
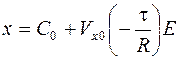При t = 0, x = 0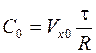 
,
. (4.24)
Решая для проекций на ось y,
; 
; 
.
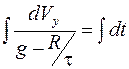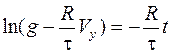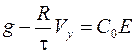При t = 0, V y = V y0, C 0 = g – R /τ× V y0
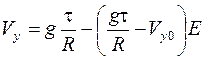(4.25)
или
,
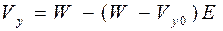где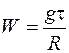 
. (4.26)
Решая
, 
.
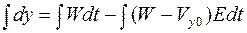При t = 0, y = 0
;
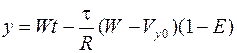. (4.27)
