Определение 7. Векторы называются компланарными, если их можно отложить в одной плоскости.
Свойства компланарных векторов.
10. Коллинеарные векторы компланарны. Иными словами, во множество всех возможных компланарных между собой векторов вместе с каждым его вектором входят все векторы, коллинеарные с ним. В частности, нулевой вектор содержится в любом таком множестве и вместе с каждым вектором в это множество входит противоположный ему вектор. Отсюда же следует, что множество компланарных векторов замкнуто относительно операции умножения на действительное число.
20. Сумма двух векторов есть вектор, компланарный с ними. Следовательно, множество компланарных векторов замкнуто относительно операции сложения.
30. Три вектора компланарны тогда и только тогда, когда хотя бы один из них можно представить в виде линейной комбинации двух других.
Доказательство. Þ Пусть векторы 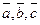 компланарны. Возможны два случая.
компланарны. Возможны два случая.
1) Среди данных векторов есть хотя бы одна пара коллинеарных векторов. Пусть  и
и  коллинеарны. Тогда, по свойствам коллинеарных векторов, хотя бы один из них можно выразить через другой. Пусть
коллинеарны. Тогда, по свойствам коллинеарных векторов, хотя бы один из них можно выразить через другой. Пусть 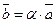 . Тогда
. Тогда 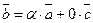 , т.е. вектор
, т.е. вектор  есть линейная комбинация векторов
есть линейная комбинация векторов  и
и 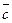 .
.
2) Данные векторы попарно не коллинеарны. Отложим их от одной точки О. Пусть 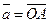 , , 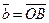 , , 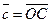 . Отрезки ОА, ОВ, ОС попарно не параллельны. Проведём СD ïïОА так, что D Î ОВ (прямой ОВ). Тогда . Отрезки ОА, ОВ, ОС попарно не параллельны. Проведём СD ïïОА так, что D Î ОВ (прямой ОВ). Тогда 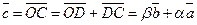 , т.е. вектор , т.е. вектор 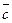 есть линейная комбинация векторов есть линейная комбинация векторов  и и  . . | 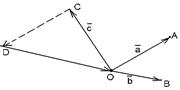 Рис. 7 Рис. 7 |
Ü Пусть 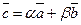 . По свойствам 10 и 20 следует, что вектор
. По свойствам 10 и 20 следует, что вектор 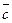 компланарен с векторами
компланарен с векторами  и
и  .
.
40. Если векторы  и
и  не коллинеарны, то любой компланарный с ними вектор можно представить в виде их линейной комбинации.
не коллинеарны, то любой компланарный с ними вектор можно представить в виде их линейной комбинации.
50. Из свойств 10 и 20 следует, что множество всех возможных компланарных векторов относительно операций сложения векторов и умножения вектора на действительное число ведёт себя так же, как множество всех коллинеарных векторов и как множество всех геометрических векторов. Кроме того, для задания множества всех возможных компланарных векторов достаточно задать любые два не коллинеарные из них.
Задача 3.
 2014-01-25
2014-01-25 1608
1608








