Уравнения вида:
 , где
, где  называется д.у. в полных дифференциалах. Левая часть уравнения, в этом случае, есть полный дифференциал от некоторой функции U(x,y):
называется д.у. в полных дифференциалах. Левая часть уравнения, в этом случае, есть полный дифференциал от некоторой функции U(x,y):
 , т.к.
, т.к. 
 тогда
тогда  - общий интеграл д.у.
- общий интеграл д.у.
Функция  может быть найдена следующим образом:
может быть найдена следующим образом:
 , проинтегрируем его по x, считая y- фиксированным. Однако и
, проинтегрируем его по x, считая y- фиксированным. Однако и  , т.е.
, т.е.
(*) 
Затем, из равенства

находим  , подставив которую в (*), определим U(x,y).
, подставив которую в (*), определим U(x,y).
Пример.

1) Убедимся, что это уравнение в полных дифференциалах:

2) 
Д.у. 1-го порядка не разрешенные относительно 
a)  б)
б) 
Предполагается, что:
1) Они не могут быть разрешены относительно 
2) Они не могут быть разрешены относительно x (a) или y (б), либо обе –  - могут быть выражены через некоторый параметр “ t ”. Иными словами
- могут быть выражены через некоторый параметр “ t ”. Иными словами
 )
) 
 )
) 
 )
) 
 )
) 
Причем в последних случаях:

Метод показывается на примерах:
1) 
Обозначим  , тогда
, тогда  , но
, но  ,
,
следовательно 

|
|
|
2)  тогда
тогда  , но
, но
 и т.д.
и т.д.
3. Д.у. 2-го порядка. Интегрирование методом понижения порядка.
3.1. Общие положения.
Д.у. 2-го порядка в общем случае имеет вид:

График всякого решения – интегральная кривая. Д.у. 2-го порядка устанавливает связь между x, y интегральной кривой, угловым коэффициентом касательной  к этой кривой и ее производной
к этой кривой и ее производной

в этой же точке.
Проинтегрировать – найти вес решения.
Задача Коши:  при
при 
Теорема Коши.
Если в д.у. 2-го порядка, разрешенном относительно  , т.е.
, т.е. 
,  - непрерывна во всей области
- непрерывна во всей области  , а ее частные производные
, а ее частные производные
 и
и  - существуют и ограничены то для любого
- существуют и ограничены то для любого  существует решение д.у. 2-го порядка, удовлетворяющее начальным условиям и такое решение единственное.
существует решение д.у. 2-го порядка, удовлетворяющее начальным условиям и такое решение единственное.
Решение задачи Коши – частное решение д.у. 2-го порядка.
Если менять  , т.е. ………, то любому
, т.е. ………, то любому  при фиксированных
при фиксированных  будет соответствовать своя интегральная кривая. Получаем пучок, образующий однопараметрическое семейство
будет соответствовать своя интегральная кривая. Получаем пучок, образующий однопараметрическое семейство  . Одновременное изменение
. Одновременное изменение  дает двухпараметрическое семейство:
дает двухпараметрическое семейство: 
Это семейство является общим решением д.у. 2-го порядка.
Опр. Общим решением д.у. 2-го порядка называют такое его решение, содержащее 2 произвольных константы, из которого выбором значений  можно получить решение любой задачи Коши, поставленной для этого д.у. в области, где такое решение существует.
можно получить решение любой задачи Коши, поставленной для этого д.у. в области, где такое решение существует.
Отсюда следует, что для получения нужного решения задачи Коши следует
определить  .
.
Пример.
 , чтобы найти решение
, чтобы найти решение  ……..
……..
получим  - частное решение.
- частное решение.
|
|
|
3.2. Интегрирование простейших д.у. 2-го порядка.
К двум типам д.у. 2-го порядка: не содержащим явно неизвестную функцию или аргумент применяют метод понижения порядка:
1-й Тип: (*) 
Введем 
(**)  - д.у. 1-го порядка относительно p.
- д.у. 1-го порядка относительно p.
Допустим, что (**) можно проинтегрировать и его общий интеграл

Заменяя в нем p на  получим д.у. 1-го порядка относительно
получим д.у. 1-го порядка относительно 

Если и это д.у. можно проинтегрировать, то его общее решение
 и будет решением (*).
и будет решением (*).
При интегрировании (*) этим методом решение находят часто в виде  или в параметрическом виде:
или в параметрическом виде:

(Параметром может служить и  )
)
Фактически данный метод сводится к интегрированию системы:

Примеры.
1)

Т.к. требуется найти только частное решение 

2)  - с разделяющимися перемнными
- с разделяющимися перемнными

2-й Тип:  Введем новую переменную
Введем новую переменную  , а
, а 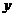 - за новую переменную. Тогда:
- за новую переменную. Тогда:
 тогда
тогда
(***) 
Допустим, что (***) проинтегрировано, тогда
 или
или
 - уравнение 1-го порядка.
- уравнение 1-го порядка.
Интегрируя последнее, получим:
 - или общее решение
- или общее решение
 - общий интеграл
- общий интеграл
Либо в параметрической форме:

Примеры.

 - Это уравнение в полных дифференциалах.
- Это уравнение в полных дифференциалах.

Интеграл тогда запишется следующим образом:
 или
или  т.к.
т.к.  , то получим:
, то получим:
(A) 

Введем параметр следующим образом:  подставляя в (А), получим:
подставляя в (А), получим:
 и тогда
и тогда 
Дифференцируем y по t

Но 


Пример 2. Проинтегрируем задачу Коши:

 - уравнение с разделяющимися переменными.
- уравнение с разделяющимися переменными.
 - общий интеграл.
- общий интеграл.
Определяем  :
:  или
или 
 или
или 
9. Линейные д.у..
9.1. Введение.
Линейное д.у. n-го порядка имеет вид:
(1) 
где y – неизвестная функция аргумента x,  - заданные непрерывные функции. Линейное д.у. называется однородным, если
- заданные непрерывные функции. Линейное д.у. называется однородным, если  .
.
При  - уравнение неоднородно, или уравнение с правой частью.
- уравнение неоднородно, или уравнение с правой частью.
Задачу нахождения решения, отвечающего условиям:
 при
при  называют задачей Коши для д.у. n-
называют задачей Коши для д.у. n-
го порядка.
Теорема Коши: Если в д.у. n-го порядка

функция F непрерывна, а ее частные производные по  ограничены во всех точках (n+1) – мерной области
ограничены во всех точках (n+1) – мерной области  , то для любого
, то для любого  существует единственное решение
существует единственное решение  данного д.у., удовлетворяющее начальным условиям.
данного д.у., удовлетворяющее начальным условиям.


Такое решение называют частным решением, соответствующим заданным начальным условиям.
Общим решением д.у. n-го порядка  (определенным на D, где выполнены условия теоремы Коши) называют решение этого уравнения, зависящего от n произвольных постоянных
(определенным на D, где выполнены условия теоремы Коши) называют решение этого уравнения, зависящего от n произвольных постоянных
 и являющихся совокупностью всех частных решений данного д.у.. Существование общего решения также гарантируется теоремой Коши, при соблюдении ее условий.
и являющихся совокупностью всех частных решений данного д.у.. Существование общего решения также гарантируется теоремой Коши, при соблюдении ее условий.
Для получения частного из общего необходимо найти  . Естественно, что условия теоремы Коши выполняются для линейного д.у. n-го порядка в области непрерывности его коэффициентов. Расшифровать!
. Естественно, что условия теоремы Коши выполняются для линейного д.у. n-го порядка в области непрерывности его коэффициентов. Расшифровать!
9.2. Линейные однородные д.у. 2-го порядка.
9.2.1. Теоремы о частных решениях.
Рассмотрим линейное однородное д.у. 2-го порядка:
(2) 
Имеют место следующие теоремы:
Теорема 1. Всякая линейная комбинация 
 нескольких частных решений
нескольких частных решений  однородного д.у. 2-го порядка также является его решением.
однородного д.у. 2-го порядка также является его решением.
|
|
|
Доказательство: Подставляя y в (2) и группируя:

т.к  теорема доказана.
теорема доказана.
В частности сумма и разность 2-х частных решений также является решеиями. Например  - являются решениями д.у.
- являются решениями д.у.  , т.к.
, т.к.  и
и  - решения.
- решения.
Теорема 2. Если известно одно частное решение д.у. однородного (ненулевое), то можно понизить порядок этого д.у. на единицу.
Док-во: Подстановка  , где z – новая неизвестная функция приведет к:
, где z – новая неизвестная функция приведет к:
 подставляя получим:
подставляя получим:

Далее, пусть  и
и  и разделим все уравнение на
и разделим все уравнение на  тогда:
тогда:
 , где
, где  т.е. получили д.у. 1-го порядка относительно u.
т.е. получили д.у. 1-го порядка относительно u.
9.2.2. Фундаментальная система решений однородного линейного д.у.
Определение: Ф.С.Р. однородного д.у. 2-го порядка называется всякая пара частных решений  этого уравнения, отношение которых не равно постоянной. Такие решения также называют линейно-независимыми.
этого уравнения, отношение которых не равно постоянной. Такие решения также называют линейно-независимыми.
Например:
 и
и  частные решения
частные решения  образуют
образуют
Ф.С.Р., а
 и
и  - нет.
- нет.
Если  - Ф.С.Р. то
- Ф.С.Р. то  - также будет Ф.С.Р.
- также будет Ф.С.Р.
Действительно, пусть  , где
, где 
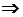
 , но тогда
, но тогда  , что и требовалось доказать.
, что и требовалось доказать.
Таким образом, если уравнение имеет одну ФСР, то оно имеет их бесконечно много. Всякое дифференциальное линейное однородное уравнение имеет нулевое решение  , но оно не входит ни в одну фундаментальную систему.
, но оно не входит ни в одну фундаментальную систему.
Определение: Определителем Вронского (вронскинианом) системы двух частных решений  и
и  уравнения (2) называют
уравнения (2) называют
 .
.
Свойства определителя Вронского:
1. Если  и
и  не образуют фундаментальной системы (т.е. являются линейно зависимыми, то их определитель Вронского тождественно равен нулю:
не образуют фундаментальной системы (т.е. являются линейно зависимыми, то их определитель Вронского тождественно равен нулю:

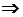
 .
.
2. Если  , то решения
, то решения  и
и  – линейно зависимы.
– линейно зависимы.
Пусть 
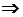
 или
или

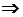
 .
.
Если 
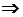

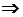
 .
.
 2018-02-14
2018-02-14 597
597








