Совместность оценок дробного факторного эксперимента

Дробный факторный эксперимент (ДФЭ) Из-за показательного роста числа экспериментов с увеличением размерности пространства 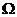ПФП оказываются практически неприемлемыми при больших . Однако из матрицы ПФП может быть отобрана некоторая часть, называемая дробным факторным планом (ДФП), которая сохраняет свойство ортогональности. Правило построения ДФП состоит в следующем. Задается порядок дробности . Из входных переменных отбирают n - p переменных (их называют основными), и для них строят полный факторный план . Этот план затем дополняют столбцами, соответствующими оставшимся переменным. Для определения способа образования этих столбцов вводится понятие генератора (генерирующего соотношения) плана. Генератор представляет собой произведение граничных значений () основных переменных, определяющее граничные значения элементов каждого из дополнительных столбцов матрицы плана. Так, для построения линейной модели от трех переменных можно воспользоваться ДФП типа с генератором :

Чем выше размерность пространства 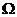, тем большее число генераторов плана можно предложить. Целесообразно выбирать такие из них, которые соответствуют незначимым взаимодействиям. Действительно, в состав базисных функций входят и левая и правая части генератора и, поскольку от эксперимента к эксперименту они меняются одинаковым образом, различить эффекты, соответствующие частям генератора, не представляется возможным. Так, если в качестве генератора выбрано соотношение , то получить раздельные оценки для и нельзя. Соответствующий ДФП позволяет оценить лишь суммарное воздействие линейного фактора и тройного взаимодействия . Подобные оценки называют смешанными. Однако, если взаимодействие незначимо, т.е. , то будет практически несмешанной оценкой. Для определения порядка смешивания вводят понятие контраста плана. Контраст – это генерирующее соотношение, задающее элементы столбца свободного члена матрицы . (Со свободным членом уравнения регрессии связывается фиктивная переменная , тождественно равная единице.) Контраст получают из генерирующего соотношения умножением на переменную, стоящую слева от знака равенства. Для ДФП с генератором контраст есть , так как . Чтобы определить, с какими переменными или взаимодействиями смешана оценка некоторой данной переменной, необходимо умножить обе части контраста на эту переменную. При этом получают порядок смешивания оценок коэффициентов при использовании данного плана.

Пусть, к примеру, исследуется объект из трех переменных полная модель которого есть

(В выражении (6.3) и далее случайное возмущение опускается.) В ходе исследования было решено ограничиться линейным (по переменным) описанием

, (6.4)

что дало основание воспользоваться ДФЭ с генератором с определяющим контрастом . Порядок смешивания для переменных следующий: , , . (6.5)

С учетом (6.5) сгруппируем подобные члены в модели (6.3): . (6.6)

Сравнивая (6.6) и (6.4), видим, что при оценивании линейной модели (6.4) получаются не чистые оценки свободного члена и линейных эффектов а оценки комбинаций, включающих двойные и тройные (для свободного члена) эффекты: .

Таким образом, платой за сокращение числа экспериментов стала совместность оценок. Если же поставить дополнительно четыре эксперимента с генератором , то получим оценки

Восемь оценок дают возможность получить раздельные оценки эффектов. Так, есть оценка , а – оценка и так далее. Это и понятно, поскольку две серии экспериментов с генераторами и дают вкупе полный факторный эксперимент, который обеспечивает раздельное оценивание коэффициентов.

В отсутствии априорной информации о значимости взаимодействий предпочтение отдается генераторам, отвечающим взаимодействиям высокого порядка, поскольку коэффициенты регрессии при них по абсолютной величине, как правило, меньше.

К достоинствам факторных планов следует отнести их хорошие точностные свойства. Легко доказать, что они являются D-, G-, A - оптимальными. К примеру, у ПФП , используемого для оценки коэффициентов модели вида , матрица плана X и матрица значений базисных функций F имеют вид:

, .

Отсюда , а . Левая часть выражения (6.2) примет вид , поскольку . Максимум этой формы достигается в вершинах квадрата: , и равняется четырем. Число оцениваемых коэффициентов (k +1) также четыре. Следовательно, условие (6.2) выполняется.

Алгоритм k -средних.

Метод k -средних в кластерном анализе.

Задача кластерного анализа носит комбинаторный характер. Прямой способ решения такой задачи заключается в полном переборе всех возможных разбиений на кластеры и выбора разбиения, обеспечивающего экстремальное значение функционала. Такой способ решения называют кластеризацией полным перебором. Аналогом кластерной проблемы комбинаторной математики является задача разбиения множества из n объектов на m подмножеств. Число таких разбиений обозначается через S (n, m) и называется числом Стирлинга второго рода. Эти числа подчиняются рекуррентному соотношению: .

При больших n .

Из этих оценок видно, что кластеризация полным перебором возможна в тех случаях, когда число объектов и кластеров невелико.

К решению задачи кластерного анализа могут быть применены методы математического программирования, в частности динамического программирования. Хотя эти методы, как и полный перебор, приводят к оптимальному решению в классе всех разбиений, для задач практической размерности они не используются, поскольку требуют значительных вычислительных ресурсов. Ниже рассматриваются алгоритмы кластеризации, которые обеспечивают получение оптимального решения в классе, меньшем класса всех возможных разбиений. Получающееся локально-оптимальное решение не обязательно будет оптимальным в классе всех разбиений.

Наиболее широкое применение получили алгоритмы последовательной кластеризации. В этих алгоритмах производится последовательный выбор точек-наблюдений и для каждой из них решается вопрос, к какому из m кластеров ее отнести. Эти алгоритмы не требуют памяти для хранения матрицы расстояний для всех пар объектов.

Остановимся на наиболее известной и изученной последовательной кластер-процедуре – методе k -средних (k -means). Особенность этого алгоритма в том, что он носит двухэтапный характер: на первом этапе в пространстве Е_n ищутся точки – центры клacтеров, а затем уже наблюдения распределяются по тем кластерам, к центрам которых они тяготеют. Алгоритм работает в предположении, что число m кластеров известно. Первый этап начинается с отбора m объектов, которые принимаются в качестве нулевого приближения центров кластеризации. Это могут быть первые m из списка объектов, случайно отобранные m объектов, либо m попарно наиболее удаленных объектов.

Каждому центру приписывается единичный вес. На первом шаге алгоритма извлекается первая из оставшихся точек (пометим ее как ) и выясняется, к какому из центров она оказалась ближе всего в смысле выбранной метрики d. Этот центр заменяется новым, определяемым как взвешенная комбинация старого центра и новой точки. Вес центра увеличивается на единицу. Обозначим через n -мерный вектор координат i -го центра на -м шаге, а через – вес этого центра. Пересчет координат центров и весов на -м шаге при извлечении очередной точки осуществляется следующим образом:

(9.5)

(9.6)

При достаточно большом числе классифицируемых объектов имеет место сходимость векторов координат центров кластеризации к некоторому пределу, то есть, начиная с некоторого шага, пересчет координат центров практически не приводит к их изменению.

Если в конкретной задаче устойчивость не имеет места, то производят многократное повторение алгоритма, выбирая в качестве начального приближения различные комбинации из m точек.

После того как центры кластеризации найдены, производится окончательное распределение объектов по кластерам: каждую точку , i =1,2,…, N относят к тому кластеру, расстояние до центра которого минимально.

Описанный алгоритм допускает обобщение на случай решения задач, для которых число кластеров заранее неизвестно. Для этого задаются двумя константами, одна из которых называется мерой грубости, а вторая Ψ₀ – мерой точности.

Число центров кластеризации полагается произвольным (пусть ), а за нулевое приближение центров кластеризации выбирают произвольные точек. Затем производится огрубление центров заменой двух ближайших центров одним, если расстояние между ними окажется меньше порога . Процедура огрубления заканчивается, когда расстояние между любыми центрами будет не меньше . Для оставшихся точек отыскивается ближайший центр кластеризации, и если расстояние между очередной точкой и ближайшим центром окажется больше, чем Ψ₀, то эта точка объявляется центром нового кластера. В противном случае точка приписывается существующему кластеру, координаты центра которого пересчитываются по правилам, аналогичным (9.5), (9.6).

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 8

D -оптимальные планы на отрезке.

Критерий D-оптимальности Критерий D -оптимальности требует такого расположения точек в области планирования 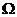, при котором определитель матрицы имеет минимальную величину. Иными словами, план D -оптимален, если .

Известно, что объем эллипсоида рассеяния пропорционален корню из величины определителя ковариационной матрицы, т.е. . С учетом (3.8) V ~ .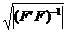

Чем меньше величина определителя, тем меньше, как правило, разброс оценок коэффициентов относительно их математических ожиданий. Исключением является случай, когда эллипсоид рассеяния имеет сильно вытянутую форму.