Түзудің параметрлік теңдеуі:
 .
.
Кеңістіктің теңдеуі. Кеңістіктегі жазықтықтың және түзудің теңдеуі, және оның түрлері. Нүктеден жазықтыққа дейінгі қашықтық.
Анықтама. Жазықтық – x,y,z айнымалыларына байланысты координаталары бірінші дәрежелі теңдеуді қанағаттандыратын, кеңістіктегі нүктелердің геометриялық орны болып табылады.
Ax+By+Cz+D = 0 (1) – жазықтықтың жалпы теңдеуі.
Жазықтықтың теңдеуі. Жазықтықтың теңдеуін құру үшін осы жазықтықта  нүкте және жазықтыққа перпендикуляр болатын
нүкте және жазықтыққа перпендикуляр болатын  векторы берілсін.
векторы берілсін.
M(х,y,,z) жазықтықтың кез келген нүктесі, онда  векторы
векторы  векторына перпендикуляр, және
векторына перпендикуляр, және 
 , онда
, онда  (скалярлық көбейтінді) координаталар түрінде
(скалярлық көбейтінді) координаталар түрінде

Бұл жазықтықтың теңдеуі. Теңдеуді түрлендіріп 
теңдеуіне келеміз, мұнда  жазықтықтың жалпы теңдеуі.
жазықтықтың жалпы теңдеуі.
|
|
|
Мысал.  нүктеден өтетін және
нүктеден өтетін және  векторына перпендикуляр болып өтетін жазықтықтың теңдеуін жазу керек.
векторына перпендикуляр болып өтетін жазықтықтың теңдеуін жазу керек.
Шешімі: (3.22) теңдеуді пайдалансақ 
Жазықтықтың толық емес теңдеулері. Енді жазықтықтың  жалпы теңдеуінің кейбір дербес жағдайларын қарастырайық:
жалпы теңдеуінің кейбір дербес жағдайларын қарастырайық:
а)  , онда
, онда  жазықтығы координата жүйесінің бас нүктесінен өтеді.
жазықтығы координата жүйесінің бас нүктесінен өтеді.
б) С=0 болсын, онда Ах+Ву+С=0 жазықтығы 0z осіне параллель болады.
в) С=0, D=0 онда Ах+D=0 немесе  координаталық жазықтығына параллель болады.
координаталық жазықтығына параллель болады.
е) Егер  және
және  ≠0 болса онда Ах=0, х=0 теңдеуі OYZ координаталық жазықтығының теңдеуі болады.
≠0 болса онда Ах=0, х=0 теңдеуі OYZ координаталық жазықтығының теңдеуі болады.
Осылай талқылап y=0 XOZ, z=0 XOY координаталық жазықтықтарының теңдеулерін жазады. Егер А≠0 В≠0 С≠0 D≠0 болса онда жазықтықтың жалпы теңдеуін мынадай  түріне келтіруге болады. Мұнда
түріне келтіруге болады. Мұнда  деп белгілесе
деп белгілесе 
теңдеу түріне келеміз. Бұл жазықтықтың кесінділер арқылы берілген теңдеуі деп аталады.
Мысал-12: Жазықтықтың теңдеуін  кесіндінің теңдеуі түріне келтір.
кесіндінің теңдеуі түріне келтір.
Шешімі: Осьтерді кесіп өтетін жазықтықтың кесінділер  шамаларын табу:
шамаларын табу:

 .
.
Жазықтықтың нормаль теңдеуі. Жазықтықтың нормаль теңдеуі деп  теңдеуін айтады. Мұнда р>0 шамасы координаталар басынан берілген жазықтыққа түсірілген перпендикулярдың ұзындығы, ал
теңдеуін айтады. Мұнда р>0 шамасы координаталар басынан берілген жазықтыққа түсірілген перпендикулярдың ұзындығы, ал  - сол перпендикулярдың координаталар осьтерінің оң бағыттарымен жасайтын бұрыштары. Егер жазықтық жалпы Ax+By+Cz+D=0 теңдеумен берілсе, оны нормальдық түріне келтіру үшін, теңдеуді
- сол перпендикулярдың координаталар осьтерінің оң бағыттарымен жасайтын бұрыштары. Егер жазықтық жалпы Ax+By+Cz+D=0 теңдеумен берілсе, оны нормальдық түріне келтіру үшін, теңдеуді  санына көбейту керек яғни
санына көбейту керек яғни  Екі (3.25) және (3.26) теңдеулерін салыстырса
Екі (3.25) және (3.26) теңдеулерін салыстырса 
|
|
|
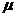 - нормалаушы көбейткіш деп атайды, оны (3.27) теңдіктерінен табамыз:
- нормалаушы көбейткіш деп атайды, оны (3.27) теңдіктерінен табамыз: 

Мұнда 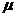 -дің таңбасы D-нің таңбасына қарама-қарсы алынады. Осы
-дің таңбасы D-нің таңбасына қарама-қарсы алынады. Осы
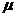 -дің мәнін (3.26) теңдеуіне қойса, келесі теңдеуге келеміз:
-дің мәнін (3.26) теңдеуіне қойса, келесі теңдеуге келеміз: 
 нүктесінен жазықтыққа дейінгі қашықтығын табу үшін, осы нүктенің координаталарын нормальдық теңдеуіне қойып, содан шыққан нәтижесінің абсолют шамасын алады, яғни
нүктесінен жазықтыққа дейінгі қашықтығын табу үшін, осы нүктенің координаталарын нормальдық теңдеуіне қойып, содан шыққан нәтижесінің абсолют шамасын алады, яғни 
20. Кеңістіктегі түзудің жалпы теңдеуі. Кеңістікте түзу бірінші дәрежелі екі теңдеумен анықталады: 
Үш белгісізі бар, екі сызықтық теңдеулер кеңістіктегі түзудің жалпы теңдеуін анықтайды, егер  ≠
≠  ≠
≠  болса.
болса.
Жазықтықтардың бір түзуден өтетін жиынын жазықтықтар шоғы деп атайды. Теңдеу 
жазықтықтар шоғының теңдеуі.
21. Кеңістіктегі түзу сызықтың канондық теңдеуі.
Айталық, түзуде  нүкте және осы түзуге параллель
нүкте және осы түзуге параллель  векторы берілсін.
векторы берілсін.  - түзудің бағыттаушы векторы деп аталады. Түзуде M(x,y,z) кез келген нүкте алайық, онда
- түзудің бағыттаушы векторы деп аталады. Түзуде M(x,y,z) кез келген нүкте алайық, онда  II
II  . Екі вектордың параллельдік шартты бойынша
. Екі вектордың параллельдік шартты бойынша 
теңдеуі анықталады. (3.32) түзу сызықтың канондық теңдеуі.
22. Түзу мен жазықтықтың кеңістікте өзара орналысуы. Екі жазықтық арасындағы бұрыш  формуласымен анықталады. Егер екі жазықтық өзара перпендикуляр болса онда
формуласымен анықталады. Егер екі жазықтық өзара перпендикуляр болса онда 
Ал екі жазықтық өзара параллель болса, онда 
Жазықтық  ал түзу сызық
ал түзу сызық  теңдеулерімен берілсе, онда
теңдеулерімен берілсе, онда 
Жазықтық пен түзудің арасындағы параллельдік (3.36) және перпендикулярлық (3.37) шарттары.
Мысал.  түзуімен
түзуімен  жазықтықтығының қиылысу түзуінен өтетін жазықтықтығының теңдеуін құру керек.
жазықтықтығының қиылысу түзуінен өтетін жазықтықтығының теңдеуін құру керек.
Шешімі. Жазықтықтар шоғының теңдеуін құрайық 
жазықтықтың түзуге параллель болатын шартын (3.36) қолданып  ,
, 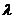 -ны табымыз, яғни
-ны табымыз, яғни 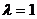 , онда ізделінген теңдеу
, онда ізделінген теңдеу  .
.
Плоскость, проходящая через точку M(x0,y0,z0):
A(x-x0) +B(y-y0)+C(z-z0)= 0 (3), с нормальным вектором N=(A,B,C).
Пример-13: Даны точки  . Написать уравнение плоскости, проходящей через точку М1 и перпендикулярной к вектору
. Написать уравнение плоскости, проходящей через точку М1 и перпендикулярной к вектору  .
.
Решение: Уравнение связки плоскостей, проходящих через точку М1, будет
 . Нормальный вектор искомой плоскости
. Нормальный вектор искомой плоскости  имеет координаты
имеет координаты  . Подставив их на место
. Подставив их на место  в уравнение связки, получим:
в уравнение связки, получим:
 или
или  . Это и есть уравнение искомой плоскости.
. Это и есть уравнение искомой плоскости.
x cosα + y cosβ + cosγ = p (4) – уравнение плоскости в нормальном виде и  - нормирующий множитель.
- нормирующий множитель.
Пример-14: Привести уравнение  к нормальной форме.
к нормальной форме.
Решение:  , то нормальное уравнение имеет вид
, то нормальное уравнение имеет вид
 .
.
 (5)-уравнение плоскости, проходящей через три заданные точки.
(5)-уравнение плоскости, проходящей через три заданные точки.
Пример-15: Написать уравнение плоскости, проходящей через точки  и
и  .
.
Решение:


 Пусть произвольная точка
Пусть произвольная точка 
 М2 лежит на искомой плоскости. Для этого
М2 лежит на искомой плоскости. Для этого

 М1 М необходимо и достаточно, чтобы векторы
М1 М необходимо и достаточно, чтобы векторы
М3  были компланарны
были компланарны
 или чтобы (рис.8.):
или чтобы (рис.8.):
рис.8.
 .
.
Расстояние от точки M(x0,y0,z0) до плоскости (1): d =  (6).
(6).
Пример-16: Найти расстояние точки  от плоскости
от плоскости 
|
|
|
Решение:  .
.
 , где t – параметр (7). Это параметрическое уравнение прямой в пространстве.
, где t – параметр (7). Это параметрическое уравнение прямой в пространстве.
 , где
, где 
 (8)- каноническое уравнение прямой.
(8)- каноническое уравнение прямой.
В общем виде общее уравнение прямой:  (9).
(9).
Әдебиеттер тізімі.
Негізгі әдебиеттер:
1. Экономистерге арналған жоғары математика. Н.Ш.Кремер редакциясы, М.,1997ж.
2. Д. Письменный Жоғары математика бойынша лекциялар конспектісі, 1 бөлім, Москва, 2004 ж.
3. Г.Н. Яковлев Математика для техникумов, 2 бөлім, М., 1978ж.
4. А.П. Рябушко Сборник индивидуальных заданий по высшей математике, Минск, 1990 ж.
5. Жоғары математика бойынша бақылау жұмыстары.
Қосымша әдебиеттер:
1. Н.Ш. Крамер Жоғары математика бойынша практикум, М., 2005 ж.
2. Шипачев В.М. Жоғары математика, т.1,2. М.,1985ж.
3. А.Н. Колесников Краткий курс математики для экономистов, 1997 ж.
Лекция-6. Жиын. Математикалық логика символы мен элементтері және олардың қолданылуы. Санды тізбектер және оның шегі, қасиеттері. Функция, оның берілу тәсілдері, классификациясы.
Жиын.
Математиканың негізгі ұғымдарының бірі - жиын ұғымы, оған математикалық анықтама беруге болмайды.
Жиын деп белгілі бір белгілеріне қарай ережемен (заңмен) біріктірілген түрлі заттардың тобын түсіну керек. Жиынды құратын заттарды оның элемменттері деп атайды.
Жиындарды әдетте латын алфавитінің бас әріптерімен A,B,C,X,Y....., ал олардың элементтерін кіші әріптермен a,b,c,x,y...., белгілейді.
Рационал сан деп екі бұтін санның қатынасы  , (n # 0) түрінде өрнектелетін санды айтады. Рационал сандар жиынын Q белгілейді.
, (n # 0) түрінде өрнектелетін санды айтады. Рационал сандар жиынын Q белгілейді.
Рационал санды шекті ондық бөлшек түрінде жазуға болатыны мектептен белгілі.
Кез келген периодсыз шексіз бөлшекті иррационал сан деп атайды. Иррационал сандар жиынын J деп белгілейді.
Барлық рационал және иррационал сандар жиынын нақты сандар жиыны деп атап R деп белгілейді.
 нақты сандар жиынын
нақты сандар жиынын 

 элемменттерімен толықтырып, оны кеңейтілген нақты сандар жиыны деп атайды да былай
элемменттерімен толықтырып, оны кеңейтілген нақты сандар жиыны деп атайды да былай  белгілейді.
белгілейді.
|
|
|
Нақты сандардың  жиыны берілсін.
жиыны берілсін.
10. Жиындардың теңдігі. Жоғарыда анықталған  кірістіру символы бойынша жиындардың теңдігі анықталады.
кірістіру символы бойынша жиындардың теңдігі анықталады.
Егер  және
және  жиындары үшін
жиындары үшін  және
және  кірістірулері бірдей орындалса, онда
кірістірулері бірдей орындалса, онда  және
және  жиындары тең дейді де,
жиындары тең дейді де,  символымен белгілейді.
символымен белгілейді.
20. Жиындардың қиылысуы.  және
және  жиындарының қиылысуы деп
жиындарының қиылысуы деп  жиынын, яғни
жиынын, яғни  және
және  жиындарында бірдей жататын
жиындарында бірдей жататын  элементтерінен құрылған жиын аталады.
элементтерінен құрылған жиын аталады.
30. Жиындардың біріктіруі.  және
және  жиындардың біріктіруі деп
жиындардың біріктіруі деп  жиынын, яғни
жиынын, яғни  және
және  жиындарының кемінде біреуінде жатқан элементтеріне құрылған жиынды айтады (бұған
жиындарының кемінде біреуінде жатқан элементтеріне құрылған жиынды айтады (бұған  мен
мен  -те жататын элементтер де кіреді).
-те жататын элементтер де кіреді).
40. Жиындардың айырымы.  және
және  жиындарының айырымы деп
жиындарының айырымы деп  жиыны, яғни
жиыны, яғни  жиынында жатып,
жиынында жатып,  жиынында жатпайтын
жиынында жатпайтын  элементтерінің жиыны аталады.
элементтерінің жиыны аталады.
Математикалық логика элементтері мен символдары және оның қолданылуы.
Математикалық логика символикасы. Математикалық сөйлемдер гректің кіші әрпімен белгіленеді: 
 жазуы,
жазуы, 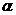 сөйлемінен
сөйлемінен  шығады.
шығады.  жазылуы,
жазылуы, 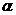 және
және  эквиваленттілігін білдіреді.
эквиваленттілігін білдіреді.
 жазуы: A-ның кез келген x элементі үшін
жазуы: A-ның кез келген x элементі үшін 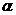 сөйлемі бар болады дегенді білдіреді.
сөйлемі бар болады дегенді білдіреді.  - кез келген.
- кез келген.
Запись  y
y  жазуы: существует элементу
жазуы: существует элементу  сөйлемінен B-ға тиісті y элементі табылады.
сөйлемінен B-ға тиісті y элементі табылады.
 – табылады.
– табылады.
 –
–  теріс емес сөйлем (не
теріс емес сөйлем (не  ).
).
Санды тізбек және оның шегі, қасиеттері. Шексіз кіші және шексіз үлкен шамалар, шексіз кіші салыстырулар, эквиваленттік.
Анықтама. Егер  санға белгілі бір ереже (заң) бойынша
санға белгілі бір ереже (заң) бойынша  нақты саны сәйкестендірілсе, онда сан тізбегі немесе жай тізбек берілген дейді.
нақты саны сәйкестендірілсе, онда сан тізбегі немесе жай тізбек берілген дейді.
Тізбекті 


 символдарының біреуімен белгілейді.
символдарының біреуімен белгілейді.
Анықтама. Егер кез келген  санына сәйкес N=N(
санына сәйкес N=N( ) саны табылып,
) саны табылып,  үшін
үшін

теңсіздігі орындалса, а санын  тізбегінің шегі деп атайды да оны былай жазады:
тізбегінің шегі деп атайды да оны былай жазады:

Шектің қасиеттері:
1. {xn  yn} тізбегі жинақты, lim(xn
yn} тізбегі жинақты, lim(xn  yn) = a
yn) = a  b.
b.
n 
 2018-02-20
2018-02-20 651
651








