Кронекер – Капелли теоремасы. 9 страница

2.  { }, b 0 тізбегі жинақты,                          lim  =

                                                                                           n

4 –теорема. {x_n}, {y_n}, {z_n} үш тізбек үшін x_n  z_n    y_n теңсіздігі орындалса және

lim x_n= a, lim y_n= b болса, онда lim z_n= a

 n    n                     n

 

{x_n}, {y_n} тізбектерін қарастырамыз:

                                                 lim (x_n±y_n)=lim x_n ± lim y_n;

                                           n→∞    n→∞ n→∞

                                   

                                                  lim x_n*y_n= lim x_n* lim y_n.

                                              n→∞  n→∞ n→∞

   

Егер                 limx_n= limy_n= 0 (y_n ≠ 0)

 тізбектерін қарастырамыз

I.  егер x_n →0, y_n →0, 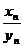 тізбектің түрі анықталмаған  болып табылады.

II. Егер x_n →∞, y_n →∞, онда да анықталмаған .

III. Егер x_n →0, y_n →∞, онда x_n * y_n  үшін, (0*∞) анықталмаған болып табылады.

IV. Егер x_n →0, y_n → – ∞, онда (x_n + y_n) тізбегі үшін, (∞ – ∞) анықталмаған болып табылады.

Тізбекті қарастырамыз:

            , табу керек:   егер n → ∞, (Эйлер), мұндағы

             е ≈ 2,718281…, яғни .         

       е –Эйлер саны немесе натурал сан деп аталады.

Анықтама. Егер 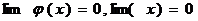  және , мұндағы х→а, онда , эквивалентті деп аталады.

 

Функция, функцияның берілу тәсілдері, классификациясы.

 

Анықтама. Е жиынындағы х -тің әрбір мәніне Е₁ жиынның нақты бір у мәнін сәйкес қоятын ереже немесе заңдылық функция деп аталады және жазылуы у = f(x), x E, мұдағы х – тәуелсіз айнымалы немесе функцияның аргументі; у – тәуелді айнымалы функция.

Айталық,  функциясы берілсін, мұндағы . Онда х – аргумент немесе тәуелсіз айнымалы, ал у – функцияның мәні немесе тәуелді айнымалы деп аталады. А жиыны функцияның анықталу облысы деп, D – деп белгілейді, ал анықталу облысынан алынған әрбір тәуелсіз айнымалыға сәйкес табылған функцияның мәндерін оның мәндерінің жиыны (Е) деп атайды.

Функцияның жоғарыда берілген анықтамасына сәйкес төмендегі 3 жағдайды анықтай білу керек:

1.  - функцияның анықталу облысын;

2. х пен у мәндерінің арасындағы ереже немесе заңдылық;

3. - функцияның мәндер жиыны.

Біз негізінен сандық функцияларды қарастырамыз, яғни анықталу облыстары мен мәндерінің жиындары санды жиындар болатын функцияларды зерттейміз.

Сандық функцияларға мысалдар:

, ;

, , ;

, .

Сандық функцияға ,  түріндегі функция да жатады.   х санының бүтін бөлігі, яғни х -тен артық емес ең үлкен сан. Мысалы, [1]=1, [1,5]=1, [-0,2]= -1, .

Функцияның берілу тәсілдері:

1. Кестелік.

2. Аналитикалық тәсіл (формуламенберілуі).

3. Графикалық тәсіл.

4. Компьютерлік (бағдарламаның көмегімен).

Функцияның негізгі түрлері (классификация):

1. 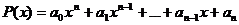- бүтін рационал функция;

2.  - бөлшек-рационал функция;

3.  - иррационал функция;

4.  - трансценденттік функция.

 

Әдебиеттер тізімі.

Негізгі әдебиеттер:

1. Экономистерге арналған жоғары математика. Н.Ш.Кремер редакциясы, М.,1997ж.

2. Д. Письменный Жоғары математика бойынша лекциялар конспектісі, 1 бөлім, Москва, 2004 ж.

3. Г.Н. Яковлев Математика для техникумов, 2 бөлім, М., 1978ж.

4. А.П. Рябушко Сборник индивидуальных заданий по высшей математике, Минск, 1990 ж.

5. Жоғары математика бойынша бақылау жұмыстары.

 

Қосымша әдебиеттер:

1. Н.Ш. Крамер Жоғары математика бойынша практикум, М., 2005 ж.

2. Шипачев В.М. Жоғары математика, т.1,2. М.,1985ж.

3. А.Н. Колесников Краткий курс математики для экономистов, 1997 ж.

Лекция-7. Шек және үздіксіз функция. Функцияның нүктедегі шегі.  

Функцияның нүктедегі және аралықтағы үздіксіздігі. Бірінші және екінші тамаша шек. Шектің қосындысы, көбейтіндісі мен қатынасы, үзілістігі. 

 

Анықтама. Функцияның 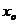 нүктесіндегі шегі деп А санын айтамыз, егер кезкелген  саны үшін қандайда бір  оң саны табылып, барлық  үшін  теңсіздігін қанағаттандыратын  теңсіздігі орындалса.

Анықтама. 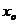  ( немесе ) нүктесіндегі  функцияның шегі деп А саны аталады, егер кез келген тізбек үшін аргументтің қабылдайтын мәндері , 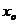-ге ұмтылатын (яғни ) болса, онда  функцияның сәйкес мәндерінің тізбегі  болғанда   А санына ұмтылады.

Бұл жағдайда  немесе  ұмтылғанда  ұмтылады.

 

Бұл анықтамалар эквивалентті.

Айталық  lim f(x_n)=A егер  n→a, мұндағы a – шексіз сан немесе  ∞.

Егер  lim f(x)=A lim φ(x)=B егер  х→a, мұндағы А және В – шексіз санба? Онда

lim[f(x)+ φ(x)]=A±B, егер х→a

lim f(x) φ(x)=AB, егер х→a

 егер В≠0, егер х→a

 

Бірінші тамаша шек:

Теорема: х = 0 нүктеде   функцияның шегі  бар болады және бірге тең, 

                                                яғни .

Бұл теңдік бірінші тамаша шек деп аталады. Бұл шектің көмегімен құрамында тригонометриялық функция енетін функциялардың щегі есептеледі.

 

Екінші тамаша шек:

Теорема: Егер х→∞,     функцияның шегі бар болады және бірге е тең,

                               яғни   немесе .

Бұл теңдік екінші тамаша шек деп аталады. Бұл шектің көмегімен құрамында х-тің дәрежелері енетін функциялардың щегі есептеледі.

Анықтама. y = f(x) функциясы х=а нүктеде үздіксіз деп аталады егер ол а нүктесінің кейбір аймағында анықталған болса: U(a), а нүктесімен бірге және х→а ұмтылғанда функция шегі бар болып және функция мәні а нүктесіне тең болса, яғни:     

1). х₀ нүктесінде анықталған;

2). U(a) аймағында анықталған

3). х→а ұмтылғанда lim f(x)=A шегі бар.

 

Анықтама.  х айнымалысы а нүктесіне а-дан артық бола отырып ұмтылса оны f (x) функциясының а нүктесіндегі оң жақты шегі деп аталады және  деп белгілейді.

х айнымалысы а нүктесіне а-дан кем бола отырып ұмтылса f (x) функциясының шегін ол нүктесіндегі сол жақтық шегі деп аталады және  деп белгілейді.  

Бұдан функцияның нүктедегі үздіксіздігінің анықтамасы шығады.

 

Анықтама. Егер y=f(x) функциясының х ®а шегі бар болып және ол х_онүктесіздігі мәніне тең болса яғни   онда f (x) функциясы а нүктесінде үзіліссіз деп аталады.

   

 

Анықтама. Егер а нүктесі y = f(х) функциясының анықталу облысында жатып және сол нүктеде f(х) үздіксіз болмаса, онда а нүктесі f(х) функциясының үзілісті нүктесі болады және осы нүктеде үзілісті деп аталады.

Анықтама. Егер а нүктесі y = f(х) функциясының анықталу облысында жатып және сол

                                                                               нүктеде f(х) үздіксіз болмаса, онда а нүктесі

               у                                                           f(x) функциясының үзілісті(сур.1.).

                                                                                нүктесі болады және осы нүктеде үзілісті

                                                                                 деп аталады. Түрлері:

                                                                                 Егер f(х) функциясының а нүктесінде

                                       а                                   х          сол жақ және оң жақ нақты

                        сур.1.                                          шектері бар болып олар өзара тең болмаса

 

онда f(х) фунгкциясын а нүктесіндегі 1-ші түрдегі үзілісті деп аталады және а нүктесін 1-ші түрдегі үзілісті нүкте деп аталады.

Егер а нүктесінде y = f(х) функциясы үшін f (а – 0) = f (а + 0) ¹ f (а) болса, онда а нүктесі жөнделетін үзілісті нүкте деп аталады.

Егер y = f(х) функциясының а нүктедегі сол және оң жақ шектерінің кемдегенде біреуінің нақты мәні болмаса, онда f(х) функциясын а нүктесіндегі 2-ші түрдегі үзілісті деп аталады және а нүктесін 2-ші түрдегі үзілісті нүкте деп аталады.

Анықтама.   f(a-0), f(a+0) егре осы шектің біреуі бар болса, онда функция екінші түрдегі

                                                                                үзілісті нүктесі бар, яғни

               у                                                           немесе

                                                                               (сур.2).

 

                                                                           түріндегі- күрделі функция

                                   а                       х        деп аталады, мұндағы - х-тің  

                                                                               функциясы.

                                      сур.2.

 

 

Әдебиеттер тізімі.

Негізгі әдебиеттер:

1. Экономистерге арналған жоғары математика. Н.Ш.Кремер редакциясы, М.,1997ж.

2. Д. Письменный Жоғары математика бойынша лекциялар конспектісі, 1 бөлім, Москва, 2004 ж.

3. Г.Н. Яковлев Математика для техникумов, 2 бөлім, М., 1978ж.

4. А.П. Рябушко Сборник индивидуальных заданий по высшей математике, Минск, 1990 ж.

5. Жоғары математика бойынша бақылау жұмыстары.

 

Қосымша әдебиеттер:

1. Н.Ш. Крамер Жоғары математика бойынша практикум, М., 2005 ж.

2. Шипачев В.М. Жоғары математика, т.1,2. М.,1985ж.

3. А.Н. Колесников Краткий курс математики для экономистов, 1997 ж.

Лекция-8. Туынды және функция дифференциалы. Туынды және жоғарғы ретті дифференциал. Туындының экономикалық мәні.

Туынды. Туындыны табу ережелері. Күрделі және кері функцияның туындысы. Параметрмен берілген функция, оның дифференциялы. Туындының кестесі.

Анықтама. Егер  шегі табылса, онда оны  нүктесіндегі  функциясының туындысы деп айтамыз, немесе  функциясы   нүктесінде дифференциалданады деп айтамыз және былай белгілейміз:  яғни,

                                    (1)

       Туындының механикалық және геометриялық мағынасы

а) Механикалық. 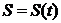 -  нүктесінің қозғалу заңы болсын.  нүктесінің -дан 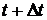-ға дейінгі аралығындағы қозғалысын қарастыралық. Онда  ал  - орташа жылдамдық. Егер

шегі табылса, онда жолдың уақыт бойынша туындысы   нүктесінің   уақыт аралығындағы қозғалысының жылдамдығына тең.

 

б) Геометриялық.   қисығында  және  нүктелерін қарастыралық.  және  екендігі анық.  нүктесін қисықтың бойымен  нүктесіне қарай жылжытамыз.  нүктесінің орналасу аралығын белгілей отырып,   қимасын аламыз. Онда  болған жағдайда  болатыны анық.

Анықтама 3.  нүктесі қисықтың бойымен   нүктесіне кез келген жағынан шексіз жақындағанда  қимасының   шектелген орны табылса, онда   қисығына  нүктесінде жүргізілген жанама деп аталады.

Е гер қисықтың жанамасы бар болса, онда  

.

Бұдан,   нүктесінде дифференциалданатын функцияның осы нүктеде бұрыштық коэффиценті  болатын жанамасы бар болады.

       Мысал 1.  функциясының  нүктесіндегі жанамасының теңдеуін жаз.

а) .  болғандықтан, жанаманың теңдеуі . -ті табалық:   

б) .  болғандықтан,  және жанаманың теңдеуі . в)

б)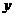

в)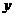

Оң жақ жанамасы  болады, яғни , ал сол жағынан жанамасы , яғни 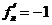. Бұдан, х=  нүктесінде берілген  функцияның туындысы табылмайды, бұл функция х=  нүктесінде үзіліссіз болғанның өзінде.