Кронекер – Капелли теоремасы. 5 страница

 

Анықтауыштың a_ij элементінің алгебралық толықтауышы деп

        санын айтады.

 

Мысалы: а₂₁, а₃₃ элементтерінің алгебралық толықтауыштары

 

А₂₁=(-1)²⁺¹ M₂₁=(-1)³ = -

 

A₃₃=(-1)³⁺³ M₃₃=(-1)⁶  =

 

     Анықтауыштың негізгі қасиеттері:

1. Анықтауыштың жолдарын оның сәйкес бағандарымен орын алмастырғаннан ол анықтауыштың сан мәні өзгермейді.
2. Егер анықтауыштың екі жолын (бағанын) бірімен-бірінің орындарын алмастырса онда анықтауыш таңбасы қарама-қарсы таңбаға ауысады.
3. Егер анықтауыштың кез-келген екі жолы өзара тең болса, онда ол нөлге тең болады.
4. Егер анықтауыштың қандай да болса бір жолының барлық элементтері нөлге тең болса, онда анықтауыш нөлге тең болады.
5. Анықтауыштың жолының немесе бағанының элементтерінің ортақ көбейткішін анықтауыш алдына шығаруға болады.
6. Егер анықтауыштың екі жолының элементтері өзара пропорционал болса онда анықтауыш нөлге тең.
7. Анықтауыштың қандай да болса бір жолының элементтерін олардың сәйкес алгебралық толықтауыштарына көбейтіп қосқаннан шыққан қосынды анықтауыш шамасына тең болады.

 .

1. Егер анықтауыштың бір жолының элементтері екі қосылғыш арқылы берілген болса, онда анықтауыш екі анықтауыштың қосындысына тең болады. Бірінші анықтауыштың сәйкес жолында бірінші қосылғыш, екінші анықтауышта екінші қосылғыш.
2. Егер анықтауыштың қандай болса да бір жолының элементтерін бір ғана санына көбейтіп басқа бір жолының сәйкес элементтеріне қосса, онда бұдан анықтауыш шамасы өзгермейді.

                   

 

 

Мысалы-3: Табу керек :

                                 .     Шешуі: . 

 

 

Матрицалар, оның түрлері. Матрицаға қолданылатын амалдар. Ранг туралы ұғым және кері матрица.   

       

Лекция 3. -өлшемді сызықтық теңдеулердің шешімі. Крамер ережесі.

Анықтама: Нақты сандардан құралған m жолы және n бағанасы бар тік бұрышты сандар кестесін A матрицасы деп атайды. Матрицаны белгілеу үшін дөнгелек не болмаса тік жақшаны қолданады, яғни

сандары матрицаның элементтері деп аталады. Егер m=n болса, яғни матрицаның жолдарының саны бағандарына тең болса, онда матрицаны n-ші ретті шаршы матрица деп атайды.

Матрица түрлері

Анықтама. Бір жатық жолдан тұратын матрицаны жатық жолды матрица деп атайды. А = (а₁,а_2,а₃... а_n).

Анықтама.  Бір тік жолдан тұратын матрицаны тік жолды матрица д.а.

В =

Анықтама.      Егер матрицаның жатық жолдары мен тік жолдарының сандары n санына тең болса, яғни өзара тең болса, онда оны n -ретті квадраттық матрица деп аталады.

 

А =

Үшінші ретті квадраттық матрица.

а_11,а_22,а₃₃... а_nm – элементтері n ретті квадрат матрицаның диагональдық элементтерін құрайды.

Анықтама.      Егер матрицаның бас диагональдарының элементтерінен басқа элементтері нөлге тең болса, онда мұндай матрицаны диагональдық матрица деп аталады. нөлге тең болса, онда мұндай матрицаны диагональдық матрица дейді.

А =

Анықтама.     Егер диагональдық матрицаның бас диагоналында тұрған элементтері бірге тең болса, онда мұндай матрицаны бірлік матрица деп аталады.

 

Е= төртінші ретті бірлік матрица.

  Анықтама.  Егер кез келген ретті матрицаның барлық элементтері нолге тең болса онда ол нольдік матрица деп аталады.

О = екінші ретті квадраттық матрица.

Матрица амалдары.

Матрицалардың негізгі амалдары ол: матрицаларды қосу, матрицалардың айырмасын анықтау, матрицаларды көбейту және матрицаны санға көбейту.

Екі өлшемдері бір А және В матрицаларының қосындысы деп сол өлшемді С=А+В матрицасын атайды. Осы С матрицаның элементтері А және В матрицаларының сәйкес элементтерінің қосындысына тең, яғни

Екі матрицаның айырмасы да осы тәсілмен анықталады, яғни  

Мысал:  және   матрицаларының қосындысын және айырмасын есептеңіз

А+В=  

А-В=  

А және В матрицаларының көбейтіндісін анықтау үшін А матрицаның і-ші жолының элементтерін В матрицаның j-ші бағанының сәйкес элементтерін көбейтіп қосады.

 Егер С=АВ болса онда

Екі матрицаны көбейтуге болады, егер бірінші А матрицаның баған саны екінші В матрицаның жол санына тең болса.

Мысал: А= және В=

матрицаларының көбейтіндісін есептеңдер.

Егер А матрицасын  санына көбейтсе, онда матрицаның әрбір элементтері осы санға көбейтіледі.

Мысал: А=  матрицасының λ= 2 санына көбейтіндісін есептеңіз.

 λА= 2 .

Матрицаны дәрежелеу.

Анықтама.  А матрицасының бүтін және оң m дәрежесі мына формуламен анықталады.

Матрицаны дәрежелеу амалы тек квадрат матрица үшін орындалады

A⁰=E, A’=A, A^m*A^k=A^m+k (A^m)^k =A^mk

 

Анықтама. Матрицаның жатық жолдарымен тік жолдарының орындарын ауыстыруды оны транспандау деп аталады. А матрицасына осы амалды қолданғанда шыққан матрицаны А' арқылы белгілейміз. А' матрицасы А матрицасының транспандалған матрицасы д.а.

A = A = A^/ - n*m

A – m*n

Транспандау амалының қасиеттері:

1⁰ (A^/)^/ =A                   3⁰ (A+B)^/ = A^/+B^/

2⁰ (λA)^/ = λ* A^/                         4⁰ (A*B)^/ = B^/*A^/

п – ретті матрицаның элементтерінен тұратын анықтаушы (2.1),   А матрицасының анықтаушысы деп аталады және белгіленуі: D=| A |.

Анықтама: Матрицаның рангы деп нольге тең емес минордың ең жоғарғы ретін айтады.

Матрицаның рангі өзгермейді, егер

1) екі жолды (бағанды) орнымен ауыстырса

2) бір жолдың (бағанның) элементтерін тұрақты нольге тең емес санға көбейтсе.

3) Бір жолдың (бағанның) элементтерін тұрақты санға көбейтіп басқа жолдың сәйкес элменттеріне қосса.

Бұндай түрлендірулер эквивалентті түрлендірулер деп айтылады. Эвивалентті түрлендіргеннен кейін берілген матрицаға эквивалентті матрица пайда болады.

Кронекер – Капелли теоремасы.

Сызықты теңдеулер жүйесінің үйлесімді, яғни шешімдері болу үшін, негізгі матрица мен кеңейтілген матрица рангыларының өзара тең болуы катетті және жеткілікті, яғни .

Рангтың белгіленуі: .

 

Кері матрица тек кана шаршы матрицаға анықталады, егер осы матрицаның анықтауышы нольге тең болмаса. Осындай матрицаға кері матрица ұғымы болады.

А^-1 матрицасы А матрицаға кері матрица деп айтылады, егер

А^-1 А=АА^-1 =Е, мұнда Е- бірлік матрица. Кері матрица келесі формуламен анықталады , мұнда

, A^*-матрицасын А матрицаға келтірілген матрица деп атайды.

Мысал:  матрицасының кері матрицасын табыңыз.

≠0. А матрицаның А_ij – алгебралық толықтауыштарын есептейміз:

А₁₁=

А₂₁

 А₁₃

 Онда кері матрица

.

 

Cызықты теңдеулер жүйесінің шешу тәсілдері.

Айталық, n белгісізді n сызықты теңдеулер жүйесі берілсін, яғни

       (2.3)

Мұндағы а₁₁а₁₂,...а_nn – теңдеулер жүйесінің коэффиценттері, - бос мүшелері деп аталады.

Жүйенің шешімін табу үшін Крамер, матрицалық және Гаусс тәсілдерін қолданамыз.

1. Крамер тәсілі. Егер (2.3) теңдеулер жүйесінің негізгі матрицасына сәйкес анықтауыш

            (2,4)

нольден ерекше ( ≠0) болса, онда теңдеулер үйлесімді және шешімі жалғыз болады.

Ол шешім Крамер формуласы бойынша анықталады, яғни             (2,5)

мұндағы  анықтауышының і-ші баған мүшелерін бос мүшелерімен ауыстыру арқылы алынған жаңа анықтауыштар.

 

1) Егер жүйенің анықтаушысы нөлге тең болмаса, онда жүйенің жалғыз ғана шешімі бар және (2.5) формуласы бойынша есептелінеді.   

2) егер D=0, онда , (2,3) жүйенің шешімі жоқ;

3) егер D=0 және , онда (2,3)  шешімі жоқ немесе шешімі шексіз.

 

Мысалы-6: Теңдеулер жүйесін шешу (Крамер ережесі бойынша):

       .         Шешуі:

             .

Таким образом: .

Матрицалық тәсіл. - өлшемді сызықтық теңдеулер жүйесін зерттеу. 

                                                       Гаусс тәсілі.

 

 белгісізі бар  сызықтық теңдеулер жүйесін қарастырамыз:    

                                       

 саны (3.1) жүйенің коэффициенті деп аталады, мұндағы:

,    ,    .

Онда    (3,2) - матрицалық теңдеу. 

(3,3) ережесі бойынша шешіледі немесе .

 

 Егер , онда         

   (3,4).

 

Мысалы-7: Теңдеулер жүйесімен матрицалық тәсілмен шешу:

                                                       

Шешуі:

Бұдан,    және

 .

 

Мысал. Матрицалық тәсілін қолданып жүйені есептеңіз.

 

 Шешімі: Мұнда А=  

Бұл тәсіл бойынша А матрицаға сәйкес кері матрицаны табамыз

, оны В баған матрицаға көбейтеміз. Онда

 

3. Гаусс тәсілі. Айталық n белгісізді n-теңдеулер жүйесі берілсін (1.5). Бұл тәсілдің негізгі мақсаты айнымалыларды біртіндеп жою. Ол үшін кеңейтілген матрицаны алып, оның негізгі бөлігін, оң жағын ескере отырып, үшбұрышты матрица түріне келтіреміз.

Бұл жағдайда кеңейтілген матрица келесі түрді қабылдайды

 Осы эквивалентті матрицаға сәйкес теңдеулер жүйесін былай жазамыз:

Осы жүйеден х_n тауып, біртіндеп жоғарылай х _n-1,х _n-2... х₂,х₁-ді табамыз.

 

Мысал: Гаусс тәсілін қолданып жүйенің шешімін табаңыз.

Шешімі.

=

=

          Осыдан

шешімін ретімен жазғанда (1; 3;  0; -2).

Көп салалы экономиканың Леонтьев моделі (баланстық талдау).

       Көпсалалы шаруашылықтың макроэкономикасы жеке салалардың арасындағы балансты керек етеді. Әрбір сала бір жағынан бұйвымды жасаушы, ал екінші жағынан басқа салалар жасайтын бұйымдарды тұтынушы болады. Бұйымдарды шығаратын және тұтынатын салалардың арасында есеп айырысуға байланысты күрделі есеп пайда болады. Бірінші рет мұндай есептің математикалық моделін жасаған белгілі америкалық экономист В.Леонтьев болды. Ол 1936 жылы Америка құрама штатында 1929-1932 жылдары болған экономикалық тоқыраудың себептеріне талдау жасады. Леонтьев моделі матрицалар алгебрасына негізделген, матрицалық талдау аппаратын қолданады.

Баланстық қатынастар

       Шаруашылықтың өндірістік ортасы әрқайсысы тек бір түрлі бұйым шығаратын саладан тұрсын. Өндірісті қамтамасыз ету үшін әрбір сала басқа салалардың бұйымдарын пайдаланады. Көп жағдайда өндіріс процесі бір уақыт аралағында қаралады. Кейде уақыт аралығы ретінде жыл алынады. Мынандай белгілеулерді енгіземіз:

х_і - і-інші саланың барлық шығаратын өнімі (жалпы жасалатын өнім).

x_ij  - i-інші саланың j-інші сала өзінің х_j – өнімін шығару үшін қолданатын өнімінің мөлшері.

у_і –і-інші саланың өндірістен тыс жерге сату үшін шығаратын өнімнің мөлшері. Мұны соңғы жұмсалыс өнімі деп атайды. Бұларға азаматтардың жеке пайдаланатын бұйымдары, қоғамдық сұранысты қанаға ттандыру, мемлекеттік иноститу ттттардың сұранымдары және тағы да басқалар жатады.

Өндірістің әртүрлі салаларының балансты принципі орындалу үшін і-інші саланың жалпы шығаратын өнімі өндіріс үшін және өндірістен тыс жерге шығаратын өнімдердің қосындысына тең болуы керек. Ең жәй түрде баланстық қатынастар

x_і = x_{і1 +} x_і2 +... + x_іn +у_і, (і = 1, 2,..., n)               1.3

түрінде беріледі. Мұны сызықтық (болжам) гипотеза немесе жай қосу деп атайды.

       (1.3) теңдеуі баланстық қатынастар деп таалады. Әр түрлі саланың өнімдерінің өлшемдері әр түрлі болғандықтан біз құндық балансты қараймыз.

 

Көпсалалы экономиканың сызықтық моделі

       АҚШ-тың екінші дүние жүзілік соғыс алдындағы экономикасын зерттеудің негізінде В.Леонть ев мынандай маңызды заңдылықты тапты: Ұзақ уақыт аралығында a_ij =         шамалары өте аз өзгерді, оларды тұрақты сандар ретінде қарастыруға болады. Өйткені өндіріс технологиясы жеткілікті ұзақ уақыт аралығында бір деңгейде тұрады, сондықтан өзінің  өнімін шығару үшін j-інші сала і-інші саланың тұрақты мөлшердегі өнімін пайдааланады. Бұл технологиялық тұрақтылық. Айтылған заңдылыққа байланысты j-інші саланың  мөлшердегі өнімін шығару үшін і-інші саланың a_ij x_і мөлгердегі өнімін пайдалану керек. Мұндағы a_ij – тұрақты сан. Мұндай жағдайда өндіріс технологиясы сызықты болады. a_ij сандары тура шығын коэфициенттері деп аталады. Сонымен сызықтық гипотеза бойынша

  x_ij = a_ij x_j; (і, j = 1, 2,..., n)                                                   1.4

 

       Мұндай жағдайда (1.3) теңдеуін теңдеулер жүйесі түрінде жазуға болады:

х₁ = а₁₁х₁ + а₁₂х₂ +... + а_1nх_n + у₁,

                           х₂ = а₂₁х₁ + а₂₂х₂ +... + а_2nх_n + у₂,                   (1.15)

.......................................................

х_n = а_n1х₁ + а_n2х₂ +... + а_nnх_n + у_n

(1.5) жүйесін матрицалық түрде жазу үшін шығарылған өнім мөлшерінің (жалпы өнім векторы), соңғы жұмсалыс мөлшерінің (соңғы пайдалану векторы) векторлық бағаналарын және тура шығын коэффициенттерінің матрицасын енгіземіз:

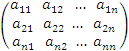 =  = ,      А =               (1.6)

Сонда (1.5) теңдеулер жүйесі

 = А  +                             (1.7)

матрицалық түрде жазылады.

       (1.7) қатынасы сызықтық салааралық баланс теңдеуі деп аталады. Бұл теңдеу (1.6) матрицаларымен бірге Леонтьев моделі деп аталады. Салааралық баланс теңдеуін екі мақсат үшін қолдануға болады. Бірінші, жалпы өнім векторы  белгілі болғанда соңғы жұмсалыс векторы  -ті табу керек. Мұндай есепті біз жоғарыда 1.5 тапсырмада қарастырғанбыз. Екінші жағдайда (1.7) теңдеуін өнеркәсіптің шығаратын жалпы өнімін жоспарлау мақсатында қолданады: Т уақыт аралығында соңғы жұмсалыс векторы  белгілі боған жағдайда жалпы өнім векторы  -ты табу керек. Мұндай жағдайда А матрицасы мен  векторын белгілі деп алып, (1.7) теңдеулер жүйесін шешеу керек. Біз енді тек осындай есептерді қарастырамыз. Мұндай есептердің экономикалық сипатынан А матрицасының және  пен  векторларының барлық элементтерінің теріс емес болтындығы шығады.