Циркуляция и ротор векторного поля

1. Циркуляция.

Пусть векторное поле образовано вектором A(P)=A_xi+A_yj+A_zk.

Возьмем в этом поле некоторую линию L и выберем на ней определенное направление. Обозначим через dS вектор, имеющий направление касательной к линии и по модулю равный дифференциалу длины дуги. Направление касательной считается совпадающим с выбранным направлением на линии. Тогда dS=dxi+dyj+dzk.

Рассмотрим криволинейный интеграл по линии L от скалярного произведения векторов A(P) и dS:

 

                          (*)

 

В силовом поле интеграл (*) выражает работу при перемещении материальной точки вдоль линии L.

Если А(Р) - произвольное векторное поле, а L - замкнутый контур, то интеграл (*) носит специальное название - циркуляция вектора.

Определение. Циркуляцией вектора А(Р) вдоль замкнутого контура L называется криволинейный интеграл по этому контуру от скалярного произведения вектора А(Р) на вектор dS касательной к контуру.

Так как скалярное произведение A(P) dS=A_S(P) dS, где A_S(P) - проекция вектора поля на направление касательной, а dS - дифференциал длины дуги, то циркуляцию можно записать в виде криволинейного интеграла по длине дуги кривой: .

Если подынтегральное выражение интеграла (*) является полным дифференциалом и векторное поле занимает область Ω, то такой интеграл по любому замкнутому контуру равен нулю. Векторные поля, в которых это условие соблюдается, мы назвали потенциальными. Следовательно, в потенциальном поле циркуляция всегда равна нулю. В произвольном векторном поле циркуляция есть некоторое число, зависящее от контура L. Пусть, например, в поле имеются замкнутые векторные линии. Выберем линию интегрирования, совпадающую с векторной линией. Тогда A_S(P)=|A(P)|u, следовательно, циркуляция, то есть _L∫|A(P)|dS, как интеграл от положительной функции, есть число заведомо положительное. Если направление интегрирования изменить на противоположное, то циркуляция станет отрицательной. Если L не является векторной линией, то циркуляция будет тем больше, чем ближе направление векторов поля А(Р) к направлениям соответствующих касательных.

Установим физический смысл циркуляции вектора в случае, когда А(Р) - поле скоростей текущей жидкости. Примем для простоты, что контур L - окружность, расположенная в некоторой плоскости. Предположим, что окружность является периферией колесика с радиальными лопатками, могущего вращаться вокруг оси, проходящей через его центр перпендикулярно к его плоскости.

Если циркуляция будет равна нулю, то колесико будет оставаться неподвижным: силы, действующие на лопатки, уравновешивают друг друга. Если циркуляция не равна нулю, то колесико будет вращаться, причем тем быстрее, чем больше величина циркуляции.

Если, например, жидкость вращается, как твердое тело, вокруг оси O_z и если ось колесика совпадает с направлением этой оси, то циркуляция равна 2wS, где S - площадь колесика. Таким образом, отношение циркуляции к площади колесика равно удвоенной угловой скорости и не зависит от размеров колесика.

Если ось колесика наклонить к оси O_z, то указанное отношение уменьшится и станет равным 2w_n, где w_n - проекция вектора на направление оси колесика. Наконец, если ось колесика станет перпендикулярной к оси вращения жидкости, то, очевидно, колесико будет неподвижным.

В случае произвольного векторного поля отношение циркуляции по плоскому контуру L к площади S, ограниченной этим контуром, будет величиной переменной.

Чтобы охарактеризовать вращательное свойство векторного поля в какой-либо его точке Р, рассмотрим предел отношения циркуляции по плоскому контуру L, окружающему точку Р, к площади S, ограниченной этим контуром, при условии, что контур L стягивается в точку Р, оставаясь в одной и той же плоскости:

 

 

Предел будет зависеть только от выбранной точки Р и от направления нормали к плоскости, в которой лежит контур L. После того как нормаль поведена к определенной стороне плоскости, направление обхода контура L вполне определено: именно обход осуществляется против часовой стрелки, если смотреть из конца нормали. Чтобы вычислить указанный предел, преобразуем выражение для циркуляции, воспользовавшись формулой Стокса:

 

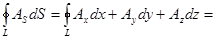
где cosα, cosβ, cosγ - направляющие косинусы нормали n, а D - область ограниченная контуром L. Последний интеграл по теореме о среднем равен произведению значения подынтегральной функции в некоторой точке Р₁ области D на величину S площади этой области.

При стягивании контура L в точку Р значение подынтегральной функции будет стремиться к её значению в точке Р. Поэтому

 

 

где значение всех частных производных берутся в точке Р. Правая часть равенства представляет собой как бы скалярное произведение двух векторов: единичного вектора n {cosα, cosβ, cosγ} - нормали к плоскости, в которой лежит контур L, и вектора, проекции которого равны

 

 

Последний вектор называется ротором или вихрем векторного поля и обозначается rotA(P).

. Ротор и его свойства.

Определение. Ротором векторного поля A(P)=A_xi+A_yj+A_zk называется вектор

 

Проекция rot_nA(P) этого вектора на любое направление дает предел отношения циркуляции вектора поля по контуру, лежащему в плоскости, проходящей через точку Р, для которой вектор n является нормалью, к площади, ограниченной этим контуром. Этот предел будет наибольшим в том случае, когда направление нормали n совпадает с направлением rotA(P).

С помощью определения ротора теорему Стокса можно сформулировать в векторной форме:

 

 

Поток ротора поля через поверхность S равен циркуляции вектора по границе этой поверхности.

Направление интегрирования по контуру L и направление нормали n к поверхности S согласованы между собой так же, как в теореме Стокса. Отсюда следует, что если две поверхности S имеют одну и ту же границу L, то потоки ротора через эти поверхности равны между собой.

Свойства.

 

1. rot [C₁A₁(P)+C₂A₂(P)]=C₁ rotA₁(P)+C₂ rotA₂(P),

 

где С₁ и С₂ - скалярные постоянные.

2. Если u(P) - скалярная функция, а А(Р) - векторная, то