Особенность задачи численного дифференцирования

Когда производную аналитически заданной функции по причине ее сложности искать трудно, или выражение для производной приобретает слишком неудобную для применения форму, используют приближенное (или численное) дифференцирование.

Этот метод становится единственным, если исходная функция задана таблично.

Пусть f(x) – функция, для которой нужно найти производную в заданной точке отрезка [a, b], а F_n(x) – интерполяционный полином для f(x), построенный на отрезке [a, b].

Заменяя f(x) интерполяционным полиномом F_n(x), получим значение производной f ’(x) на отрезке [a, b], т.е.

f ’(x)» F ’(x).                                                                       (1)

 

1. Интерполяционная формула Лагранжа для равноотстоящих узлов

Пусть функция f(x) задана на отрезке [a, b] в равноотстоящих узлах a = x₀, x₁, …, x_n = b, которыми отрезок делится на n равных частей: x_i+1 – x_i = h = const (i = 0, 1, …,n-1). В этом случае шаг интерполирования , а полином Лагранжа имеет более удобный вид. Действительно, пусть   (2) и .

Тогда

(умножим числитель и знаменатель на (x-x_i)).

Найдем все разности:

Тогда . С другой стороны, т.к. x_i = x₀ +ih, получим:

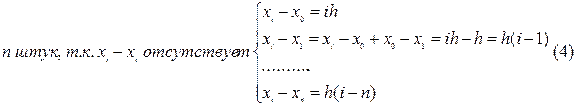
Используя (4), получим формулу для П’_n+1(x_i):

Итак, имеем:

Пример. Составить интерполяционный полином Лагранжа для функции, заданной своими значениями на равноотстоящих узлах (n=2, h=1).

x₀=2 t = x – 2 x = t + 2

x	2	3	4
f(x)	4	-2	6

 

1. Численное дифференцирование интерполяционной формулы Лагранжа

Найдем производную функции f(x):

Пример. Вычислить приближенно значение производной функции, заданной таблицей, в точке

x = 4.

x	3	4	5
f(x)	2	-1	6

 

n=2 h=1 t=x-3 x=t+3

 

 

1. Численное дифференцирование на основе интерполяционной формулы Ньютона

Запишем для функции f(x), заданной своими значениями в равноотстоящих узлах x₀, x₁, …, x_n 1-й интерполяционным полином Ньютона:

Дифференцируя по t функцию P_n(t), получим:

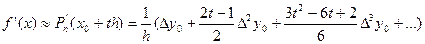 (7)

Однако, каждый раз, вычисляя значение производной f(x) в некоторой фиксированной точке x, в качестве x₀ следует брать ближайшее слева узловое значение аргумента. Формула (7) существенно упрощается, если исходное значение x оказывается одним из узлов таблицы. Так как в этом случае каждый узел можно считать начальным, то, принимая x = x₀, t = 0, получим:

(8)

Эта формула позволяет достаточно точно получать значения производных функций, заданных таблично.

Пример. Вычислить приближенно значение производной функции, заданной таблицей, в точке

x = 32.

x	32	33	34	35	36
f(x)	5,657	5,745	5,831	5,916	6,000

 

n=4 h=1

 

Построим таблицу конечных разностей:

x	y	∆y0	∆2y0	∆3y0	∆4y0
32	5,657	0,088	-0,002	0,001	-0,001
33	5,745	0,086	-0,001	0
34	5,831	0,085	-0,001
35	5,916	0,084
36	6,000

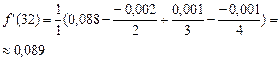
Для проверки погрешности вычислений, посчитаем значение этой функции, заданной аналитически: f(x)=

Замечаем совпадение значений в пределах двух знаков после запятой.

 

1. Постановка задачи численного интегрирования

При вычислении определенного интеграла , где f(x) – непрерывна на отрезке     [a, b] используется формула Ньютона – Лейбница:   (9), где F(x) – первообразная для функции f(x), т.е. F’(x) = f(x).

В случае, когда F(x) определить аналитически сложно (или в случае табличных значений f(x) практически невозможно), используются формулы приближенного вычисления, называемые квадратурными формулами.

Простой прием построения квадратурных формул состоит в том, что подынтегральная функция f(x) заменяется на отрезке [a, b] интерполяционным полиномом Лагранжа L_n(x) и получается приближенное равенство:   (10).

Пусть [a, b] разбит на n равных частей: a = x₀, x₁, …, x_n = b. Тогда

   (11)

Таким образом, имеем:

(12)

Замечания.

1. коэффициенты A_i не зависят от функции f(x), т.е. они составлены только с учетом узлов интерполяции.

2. если f(x) – полином степени n, то тогда формула (10) является точной, т.к. L_n(x)=f(x).