Зависимые события и условная вероятность

На предыдущем занятии мы ознакомились с основными теоремами сложения и умножения вероятностей, а также научились решать типовые задачи с независимыми событиями.

Кратко повторим, что такое независимость событий: события и являются НЕзависимыми, если вероятность любого из них не зависит от появления либо непоявления другого события. Простейший пример – подбрасывание двух монет. Вероятность выпадения орла либо решки на одной монете никак не зависит от результата броска другой монеты.

Сначала рассмотрим традиционный набор, состоящий из двух событий: событие является зависимым, если помимо случайных факторов его вероятность зависит от появления либо непоявления события . Вероятность события , вычисленная в предположении того, что событие уже произошло, называется условной вероятностью наступления события и обозначается через . При этом события и называют зависимыми событиями (хотя, строго говоря, зависимо только одно из них).

Задача 1

Из колоды в 36 карт последовательно извлекаются 2 карты. Найти вероятность того, что вторая карта окажется червой, если до этого:

а) была извлечена черва;

б) была извлечена карта другой масти.

Решение: рассмотрим событие: – вторая карта будет червой. Совершенно понятно, что вероятность этого события зависит от того, черву или не черву вытянули ранее.

а) Если сначала была извлечена черва (событие ), то в колоде осталось 35 карт, среди которых теперь находится 8 карт червовой масти. По классическому определению:

– вероятность того, что вторая карта окажется червой при условии, что до этого тоже была извлечена черва.

б) Если же сначала была извлечена карта другой масти (событие ), то все 9 черв остались в колоде. По классическому определению:

– вероятность того, что вторая карта окажется червой при условии, что до этого была извлечена карта другой масти.

Всё логично – если вероятность извлечения червы из полной колоды составляет , то при извлечении следующей карты аналогичная вероятность изменится: в первом случае – уменьшится (т.к. черв стало меньше), а во втором – возрастёт: (т.к. все червы остались в колоде).

Ответ:

Зависимых событий, разумеется, может быть и больше. Пусть 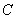– третьей картой будет извлечена черва. Предположим, что произошло событие , а затем событие ; тогда в колоде осталось 34 карты, среди которых 7 черв. По классическому определению:

– вероятность наступления события 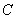при условии, что до этого были извлечены две червы.

Задача 2 См. решение

В конверте находится 10 лотерейных билетов, среди которых 3 выигрышных. Из конверта последовательно извлекаются билеты. Найти вероятности того, что:

а) 2-й извлечённый билет будет выигрышным, если 1-й был выигрышным;

б) 3-й будет выигрышным, если предыдущие два билета были выигрышными;

в) 4-й будет выигрышным, если предыдущие билеты были выигрышными.

Решение: рассмотрим события: – при 1-й, 2-й, 3-й и 4-й попытках соответственно будет извлечён выигрышный билет.

а) Пусть событие состоялось. Тогда в конверте осталось 9 билетов, среди которых 2 выигрышных. По классическому определению:

_____– вероятность того, что 2-й выбранный билет будет выигрышным при условии, что до этого извлечён выигрышный билет.

б) Если произошли события , то в конверте осталось 8 билетов, среди которых 1 выигрышный. По классическому определению:

_______– вероятность того, что 3-й выбранный билет будет выигрышным при условии, что до этого было извлечено два выигрышных билета.

в) Если произошли события , то в конверте не осталось выигрышных билетов. По классическому определению:

_______– вероятность того, что 4-й выбранный билет будет выигрышным при условии, что до этого были извлечены три выигрышных билета.

Ответ: _______________

А теперь обратим внимание на один принципиально важный момент: в рассмотренных примерах требовалось найти лишь условные вероятности, при этом предыдущие события считались достоверно состоявшимися. Но ведь в действительности и они являются случайными! Так, в задаче извлечение червы из полной колоды – есть событие случайное, вероятность которого равна .

На практике гораздо чаще требуется отыскать вероятность совместного появления зависимых событий. Как, например, найти вероятность события , состоящего в том, что из полной колоды будет извлечена черва и затем ещё одна черва? Ответ на этот вопрос даёт теорема умножения вероятностей зависимых событий: вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже произошло:

В нашем случае:

– вероятность того, что из полной колоды будут извлечены 2 червы подряд.

Аналогично: – вероятность того, что сначала будет извлечена карта другой масти и затем черва.

Вероятность события получилась заметно больше вероятности события , что, в общем-то, было очевидно безо всяких вычислений.

И, само собой, не стоит ожидать, что из конверта с десятью лотерейными билетами (Задача 2) вы вытяните 3 выигрышных билета подряд:

Да, совершенно верно – теорема умножения вероятностей зависимых событий естественным образом распространяется и на бОльшее их количество.

Закрепим материал несколькими типовыми примерами:

Задача 3

В урне 4 белых и 7 черных шаров. Из урны наудачу один за другим извлекают два шара, не возвращая их обратно. Найти вероятность того, что:

а) оба шара будут белыми;

б) оба шара будут чёрными;

в) сначала будет извлечён белый шар, а затем – чёрный.

Обратите внимание на уточнение «не возвращая их обратно». Этот комментарий дополнительно подчёркивает тот факт, что события зависимы. Действительно, а вдруг извлечённые шары возвращают обратно? В случае возвратной выборки вероятности извлечения чёрного и белого шара меняться не будут, а в такой задаче уже следует руководствоваться теоремой умножения вероятностей НЕзависимых событий.

Решение: всего в урне: 4 + 7 = 11 шаров.

а) Рассмотрим события – первый шар будет белым, – второй шар будет белым и найдём вероятность события , состоящего в том, что 1-й шар будет белым и 2-й белым.

По классическому определению вероятности: . Предположим, что белый шар извлечён, тогда в урне останется 10 шаров, среди которых 3 белых, поэтому: – вероятность извлечения белого шара во 2-м испытании при условии, что до этого был извлечён белый шар.

По теореме умножения вероятностей зависимых событий:

– вероятность того, что оба шара будут белыми.

б) Найдём вероятность события , состоящего в том, что 1-й шар будет чёрным и 2-й чёрным

По классическому определению: – вероятность того, что в 1-м испытании будет извлечён чёрный шар. Пусть извлечён чёрный шар, тогда в урне останется 10 шаров, среди которых 6 чёрных, следовательно: – вероятность того, что во 2-м испытании будет извлечён чёрный шар при условии, что до этого был извлечен чёрный шар.

По теореме умножения вероятностей зависимых событий:

– вероятность того, что оба шара будут чёрными.

в) Найдём вероятность события (сначала будет извлечён белый шар и затем чёрный)

После извлечения белого шара (с вероятностью ) в урне останется 10 шаров, среди которых 3 белых и 7 чёрных, таким образом: – вероятность того, что во 2-м испытании будет извлечён чёрный шар при условии, что до этого был извлечен белый шар.

По теореме умножения вероятностей зависимых событий:

– искомая вероятность.

Ответ:

Данную задачу нетрудно проверить через теорему сложения вероятностей событий, образующих полную группу. Для этого найдём вероятность 4-го недостающего события: – того, что сначала будет извлечён чёрный шар и затем белый.

События образуют полную группу, поэтому сумма их вероятностей должна равняться единице:

,что и требовалось проверить.

Задача 4 См. решение

Какова вероятность того, что из колоды в 36 карт будут извлечены два туза подряд?

Решение: всего: 4 туза в колоде. Рассмотрим события – первой картой будет извлечён туз, – 2-й картой будет извлечён туз. По классическому определению вероятности: .________ В случае осуществления события в колоде останется 35 карт, среди которых 3 туза, поэтому: _______ – вероятность того, что 2-й картой будет извлечён туз, при условии, что до этого был извлечен туз.

По теореме умножения вероятностей зависимых событий:

__________ – вероятность того, что из колоды в 36 карт будут извлечены два туза подряд.

Ответ: ______

Задача 5 Д/з

В урне 6 черных, 5 красных и 4 белых шара. Последовательно извлекают три шара. Найти вероятность того, что

а) третий шар окажется белым, если до этого был извлечён черный и красный шар;

б) первый шар окажется черным, второй – красным и третий – белым.

Зависимые события возникают в тех случаях, когда осуществляется некоторая цепочка действий. Однако сама по себе последовательность действий ещё не гарантируют зависимость событий. Пусть, например, студент наугад отвечает на вопросы какого-нибудь теста – данные события хоть и происходят одно за другим, но незнание ответа на один вопрос никак не зависит от незнания других ответов. Хотя, закономерности тут, конечно, есть. Тогда совсем простой пример с неоднократным подбрасыванием монеты – сей увлекательный процесс даже так и называется: повторные НЕзависимые испытания.

Задача 6

Из урны, в которой находится 6 белых и 4 черных шара, извлекаются наудачу один за другим три шара. Найти вероятность того, что:

а) все три шара будут черными;

б) будет не меньше двух шаров черного цвета.

Решение:всего: 6 + 4 = 10 шаров в урне.

а) Рассмотрим событие: – все три шара будут черными.

По теореме умножения вероятностей зависимых событий:

б) Рассмотрим событие: 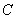– будет не меньше двух шаров черного цвета. Данное событие состоит в 2 несовместных исходах: либо все шары будут чёрными (событие ) либо 2 шара будут чёрным и 1 белым – обозначим последнее событие буквой .

Событие включается в себя 3 несовместных исхода:

в 1-м испытании извлечён белый и во 2-м и в 3-м испытаниях – чёрные шары или в 1-м испытании извлечён ЧШ и во 2-м – БШ и в 3-м – ЧШ или в 1-м испытании извлечён ЧШ и во 2-м – ЧШ и в 3-м – БШ.

По теоремам сложения вероятностей несовместных и умножения вероятностей зависимых событий: – вероятность того, что среди трёх последовательно извлеченных шаров будет 2 чёрных и 1 белый шар.

На всякий случай озвучу примерный ход рассуждений при конструировании, например, произведения : «в 1-м испытании с вероятностью извлекается ЧШ, после чего в урне останется 9 шаров, среди которых 6 белых и 3 чёрных. И во 2-м испытании с вероятностью извлекается БШ, после чего в урне останется 8 шаров, среди которых 5 белых и 3 чёрных. И, наконец, в 3-м испытании с вероятностью будет снова извлечён ЧШ»

По теореме сложения вероятностей несовместных событий: – вероятность того, что среди трёх последовательно извлеченных шаров будет не менее двух черных.

Ответ:

Задача 7 См. решение

Из 20 экзаменационных билетов 3 содержат простые вопросы. Пять студентов по очереди берут билеты. Найти вероятность того, что хотя бы одному из них достанется билет с простыми вопросами.

Решение: рассмотрим события:

– хотя бы одному из пяти студентов достанется билет с простыми вопросами;

– всем пятерым достанутся непростые билеты.

Данные события являются противоположными, поэтому .

По теореме умножения вероятностей зависимых событий:

__________________
Таким образом: _____________ – искомая вероятность

Ответ: ___________

Задача 8

В первой урне содержится 12 шаров, из них 7 белых, во второй – 6 шаров, из них 3 белых. Из первой урны во вторую наудачу перекладывают один шар, а затем из второй урны наудачу извлекают один шар. Найти вероятность того, что он окажется белым.

Решение:по условию, из первой урны во вторую наудачу перекладывают один шар, и, очевидно, он может быть как белым, так и не белым. В этой связи необходимо рассмотреть 2 несовместные гипотезы:

– из 1-й урны во 2-ю будет переложен белый шар;

– из 1-й урны во 2-ю будет переложен не белый шар.

Обозначим через зависимое событие – из 2-й урны будет извлечён белый шар.

Несовместные исходы удобно расписать по пунктам:

1) По классическому определению: – вероятность того, что из 1-й урны во вторую будет переложен белый шар. Пусть гипотеза осуществилась, тогда во второй урне стало 7 шаров, среди которых теперь 4 белых шара. Таким образом: – вероятность того, что из второй урны будет извлечен белый шар при условии, что туда был переложен белый шар.

По теореме умножения вероятностей зависимых событий:

– вероятность того, что во 2-ю урну будет переложен белый шар и после этого из 2-й урны будет извлечён белый шар.

2) По классическому определению: – вероятность того, что из 1-й урны во вторую будет переложен не белый шар. Пусть гипотеза осуществилась, тогда во второй урне стало 7 шаров, среди которых по-прежнему 3 белых. Таким образом: – вероятность того, что из второй урны будет извлечен белый шар при условии, что туда был переложен не белый шар.