2020-05-21
861
По аналогии с представлением любой функции (не равной тождественному нулю) в виде СДНФ можно функцию (не равную тождественной 1) представить в виде СКНФ: простая дизъюнкция составляется для тех наборов переменных (х 1, х 2, …, х n), для которых f (х 1, х 2, …, х n) = 0, причем если хi = 1, то в этой дизъюнкции берем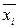 
, если же хi = 0, то берем хi.
Пример 1. Составить для импликации и сложения по модулю 2 СДНФ и СКНФ. Составим таблицу истинности для рассматриваемых функций.
5. Таблица 5 – Таблица истинности для
функций импликации и сложения по модулю два
| x | y | f1=x→y | f2=x+y |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
СДНФ для этих функций:
СКНФ для этих функций:
Пример 2. Составить СДНФ и СКНФ на примере мажоритарной системы подсчета голосов, т.е. системы, дающей сигнал «1» на выходе, если более половины сигналов на входе «1». Составим таблицу истинности для рассматриваемой функции (табл. 6).
6. Таблица 6 – Таблица истинности
| a | b | c | f | СДНФ | СКНФ | |
| 0 | 0 | 0 | 0 | 0 | 
| |
| 1 | 0 | 0 | 1 | 0 | 
| |
| 2 | 0 | 1 | 0 | 0 | 
| |
| 3 | 0 | 1 | 1 | 1 | 
| |
| 4 | 1 | 0 | 0 | 0 | 
| |
| 5 | 1 | 0 | 1 | 1 | 
| |
| 6 | 1 | 1 | 0 | 1 | 
| |
| 7 | 1 | 1 | 1 | 1 | 
|
|
|
|
В совершенной дизъюнктивной нормальной форме заданная функция записывается в виде:
т.е. функция записана для тех строк, где она обращается в 1.
В совершенной конъюнктивной нормальной форме заданная функция записывается в виде:
т.е. функция записана для тех строк, в которых она обращается в 0.
Набор функций, через которые можно выразить любые другие функции, называется полным набором. Таким образом, конъюнкция, дизъюнкция и отрицание является полным набором.
Упрощение логических выражений можно произвести с помощью методов минимизации. Для несложных функций используются алгебраические преобразования. Для более сложных с числом переменных от 3 до 6 применяют карты Карно.
