Этапы МКЭ при решении задач расчета напряженно-деформированного состояния конструкций

Лекция №8

Вариационные методы решения краевых задач.

Методы Бубнова - Галеркина и Ритца, конечных элементов.

Этапы МКЭ при решении задач расчета напряженно-деформированного состояния конструкций

 

Вариационные методы широко применяются как в теоретических исследованиях для доказательства теорем существования, единственности и устойчивости решений, в спектральной теории, при изучении разнообразных вопросов оптимизации и т.д., так и в вопросах, связанных с нахождением приближенных решений [47, 54, 66-71]. Нахождение приближенных решений вариационными методами сводится к решению систем алгебраических уравнений, при этом алгоритмы нахождения приближенных решений вариационными методами часто оказываются проще и удобнее, чем имеющиеся алгоритмы решения соответствующих задач для дифференциальных уравнений с частными производными. Для приближенного решения многих задач математической физики часто применяют такие методы как Ритца и Бубнова – Галеркина.

Вариационные методы основаны на изучении общих количественных характеристик функционалов, таких как энергия деформации, работа внешних сил при деформации конструкции и т.д. Общность анализа, возможность использования приближенных методов, удобных для численной реализации на ЭВМ, делают вариационные или энергетические методы весьма важными для прочностного анализа конструкции и в механике жидкости и газа.

Вариационные методы связаны с понятием функционала. Функционалом называется скалярная величина (число), зависящая от поведения функции или нескольких функций в определенной области. Например, длина кривой, соединяющей две заданные точки пространства, является функционалом, который имеет минимальное значение для линейной функции.

 Математическая формулировка вариационных методов

Решения многих краевых задач для дифференциальных уравнений могут быть сведены к задаче нахождения минимума некоторого функционала  при соответствующих граничных условиях, для которого исходное дифференциальное уравнение является уравнением Эйлера-Лагранжа [51, 66, 72 -73].

Методы решения дифференциальных уравнений на основе минимизации функционалов называются прямыми методами вариационного исчисления.

Пусть имеется краевая задача

                                 ,                                               (8.1)

где G граница W – области определения функции . Также могут рассматриваться для этой области граничные условия другого рода.

Если дифференциальный оператор  является положительно определенным и самосопряженным, то соответствующая вариационная постановка для краевой задачи (8.1) имеет вид:

Найти функцию , минимизирующую функционал

                               .                  (8.2)

Вариационная задача имеет определенные преимущества по сравнению с постановкой задачи (8.1): во-первых, порядок дифференциального оператора понижается в два раза; во-вторых, появляется возможность более удобного формулирования граничных условий, смягчения требований к координатным функциям; в-третьих, появляется возможность более простого представления разностных выражений.

Применительно к задачам из области механики задачи (8.1) и (8.2) можно представить в виде:

,         (8.1¢)

матрица операции дифференцирования, 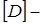матрица свойств материалов (упругости).

Тогда задачу (8.2) можно записать в виде:

. (8.2¢)

В терминах механики сплошной среды задачу (8.2¢) можно представить в виде:     ,             (8.3)

где П – потенциальная энергия системы (тела); 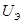– потенциальная энергия деформации системы; W – работа (возможная) внешних сил; – тензор деформации; – вектор перемещений; – матрица упругости; L – матрица операций дифференцирования; Т – транспонирование матриц.

Для плоского случая

Например, для функционалов вида ,                 (8.4)

                                                                 (8.5)

уравнения Эйлера-Лагранжа соответственно имеют вид:

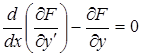                       ,                                                (8.6)

                         ,                                (8.7)

которые соответствуют дифференциальным уравнениям 2-го порядка (обыкновенным и в частных производных) при граничных условиях: а) ; б) 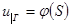. Таким образом, решение краевой задачи для дифференциального уравнения можно получить путем минимизации соответствующего функционала , поскольку функция, которая минимизирует этот функционал, является решением уравнения Эйлера-Лагранжа, соответствующего исходному дифференциальному уравнению.

Основная идея вариационных методов решения краевых задач заключается в том, что решение краевой задачи можно заменить минимизацией некоторого функционала и использовать для его решения хорошо разработанный математический аппарат численной минимизации функционалов. Наоборот, задачу минимизации функционала можно свести к исследованию краевой задачи для дифференциального уравнения. В первую очередь нужно указать функционал, для которого исследуемая краевая задача является необходимым условием экстремума.

 

Метод Ритца

Для нахождения функции , при которой значение функционала  близко к минимальному, Ритцем был предложен следующий метод (1908г.) [54].

Рассматривается семейство функций, которые зависят от нескольких параметров и удовлетворяют граничным условиям краевой задачи:

                                                                              (8.8)

Среди допустимых функций определяется та, которая дает функционалу  наименьшее значение. Эта задача является уже более легкой, чем первоначальная. Действительно, подставив в функционал  вместо  выражение  в виде (8.8) и выполнив необходимые операции дифференцирования и интегрирования, получим функцию от  параметров , т.е. .

Для определения минимума этого функционала коэффициенты  должны удовлетворять системе уравнений

                                                              (8.9)

Решение системы (8.9) для функционала ) определяет абсолютный минимум, а оптимальные значения параметров , при которых достигается абсолютный минимум, определяют искомое приближенное решение .

Практически в наиболее важных случаях в интеграле  подынтегральное выражение представляет собой многочлен второй степени относительно .

Если параметры  включены в функцию (8.8) по линейной зависимости, т.е.

   ,   (8.10)

тогда функционал является квадратичной функцией относительно параметров . В этом случае задача нахождения минимума квадратичной функции ) сводится к решению системы линейных алгебраических уравнений относительно параметров 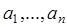. Система линейных алгебраических уравнений достаточно просто решается при  ~ 10². Практически бывает достаточным выбрать количество параметров .

Полноту системы обычно удается обнаружить, пользуясь обобщенной теоремой Вейерштрасса [54].

С помощью этой теоремы можно установить полноту следующей системы функций: пусть  - непрерывная функция, имеющая внутри области D ограниченные и непрерывные производные  и ;  внутри области D и . С учетом вышеизложенного в качестве основной системы функций (8.10) можно принять:

, , , ,

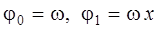Функции  называются базисными (координатными функциями).

Для области D, являющегося прямоугольником , функция  может иметь вид:

Если уравнение границы Г задана в виде:  где F - непрерывная функция вместе с частными производными, то можно принять . Иногда в качестве  берут комбинации тригонометрических функций.

 

 Метод Бубнова-Галеркина

 

Рассмотрим краевую задачу, которую можно представить в виде

                                    (8.18)

Решение задачи (8.18) будем искать в виде

                                   ,                                (8.19)

где  – система координатных функций, которые выбираются заранее и удовлетворяют граничным условиям исходной задачи (8.18),  – неизвестные коэффициенты. Функции  являются линейно независимыми и представляют собой первые  элементов некоторой полной системы координатных функций в заданной области.

Для того чтобы  было точным решением задачи (8.18), необходимо выполнение тождества , что равносильно, в случае непрерывности , требованию ортогональности выражения  ко всем координатным функциям системы 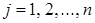. При этом, имея в своем распоряжении только  постоянных , можно удовлетворить лишь  условиям ортогональности:

. (8.20)

В результате для определения коэффициентов  получим систему из  уравнений. В случае линейного оператора  система (8.20) представляет собой систему линейных алгебраических уравнений, откуда определяются коэффициенты 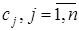. В общем случае система (8.20) является нелинейной.

При выводе системы (8.20) не были использованы вариационные принципы и метод Бубнова – Галеркина является универсальным, не требующим положительной определенности самосопряженного оператора  [65].

 Математические основы метода конечных элементов

Одним из распространенных приближенных методов решения задач математической физики является метод конечных элементов (МКЭ). Этот метод используется при решении задач строительной механики и механики сплошных сред, гидромеханики, для анализа напряжений, например, в конструкциях самолетов, автомобилей, плотин, различных оболочек и других сложных систем [66-68, 71, 74-76]. В строительной механике МКЭ позволяет минимизацией потенциальной энергии свести задачу к системе линейных уравнений равновесия. Метод может применяться к задачам, описываемым уравнениями Лапласа или Пуассона, решение которых связано также с минимизацией некоторого функционала. МКЭ является численным методом решения дифференциальных уравнений или систем дифференциальных уравнений, его можно рассматривать как один из вариантов метода Ритца. Следует также отметить, что применение МКЭ в общем виде исключает необходимость вариационной формулировки физических задач.

  Основы метода конечных элементов

 

Математическая основа метода конечных элементов (МКЭ) – вариационное исчисление, т.е. нахождение минимума функционала. С этой точки зрения МКЭ представляет собой неявное применение метода Ритца на отдельных подобластях (конечных элементах).

Основная идея метода конечных элементов состоит в том, что любую непрерывную величину можно аппроксимировать дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определенных на конечном числе подобластей. Кусочно-непрерывные функции определяются с помощью значений непрерывной величины в конечном числе точек рассматриваемой области. В общем случае непрерывная величина заранее неизвестна и нужно определить значения этой величины в некоторых внутренних точках области. Для построения дискретной модели непрерывной величины по МКЭ выполняются следующие действия:

1. В рассматриваемой области фиксируется конечное число точек. Эти точки называются узловыми точками.

2. Значение непрерывной величины в каждой узловой точке считается переменной, которая должна быть определена.

3. Область определения непрерывной величины разбивается на конечное число подобластей, называемых элементами. Эти элементы имеют общие узловые точки и в совокупности аппроксимируют форму области.

4. Непрерывная величина аппроксимируется на каждом элементе полиномом, который определяется с помощью узловых значений этой величины. Для каждого элемента определяется свой полином. Полиномы подбираются таким образом, чтобы сохранялась непрерывность величины вдоль границ элементов.

Значения непрерывной величины в узловых точках определяются таким образом, чтобы обеспечить наилучшее приближение к истинным (точным) значениям непрерывной величины путем минимизации некоторого функционала, связанного с физической сущностью задачи (с соответствующим дифференциальным уравнением). В итоге процесс минимизации сводится к решению системы линейных алгебраических уравнений относительно узловых значений непрерывной величины.

При решении прикладных задач большое значение имеет оценка погрешности приближенного метода. Приближенное решение, полученное методом конечных элементов, будет сходиться к точному решению с уменьшением размеров элемента при условии, что, как только узловые значения оказываются равными между собой, интерполяционные уравнения приводят к постоянным значениям рассматриваемых величин внутри элемента.