2020-05-25
178
и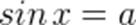 
Группа Табличных решений
Вспомним, что:
- 
— это абсцисса точки х, расположенной на единичной окружности и соответствующей углу х. Чтобы найти абсциссу точки х, расположенной на единичной окружности, опускаем перпендикуляр из этой точки на ось косинусов (ось ОХ – ось абсцисс) (Рис.Б).
- 
— это ордината точки х, расположенной на единичной окружности и соответствующей углу х. Чтобы найти ординату точки х, расположенной на единичной окружности, опускаем перпендикуляр из этой точки на ось синусов (ось ОУ – ось ординат) (Рис.Б).
Рис.Б
Дополним, что из определения синуса и косинуса следует, что уравнения 
и 
имеют решения только при условии 
. Отсюда следует, что, например, уравнения, подобные ниже указанным: sinx = 3/2 или cosx = 7 решений не имеют!
Рассмотрим группу 2 Табличных решений –
для табличных значений тригонометрических функций синус и косинус, при табличных а = + ½; -½; +√2/2; -√2/2; +√3/2; -√3/2.
Теперь в правой части уравнения будет стоять табличное значение синуса или косинуса (напомним, что решение уравнений с а= 0, ±1 были рассмотрены на предыдущем занятии).
|
|
|
1. 
Проведя вертикальную линию, перпендикулярную оси косинусов через заданное в уравнении значение cosx = ½, получим на единичной окружности вертикальную пару точек с абсциссой 1/2: это величины углов π/3 и -π/3 радиан (Рис.1).
Рис.1
Эти две точки на единичной окружности, равные π/3 и -π/3 радиан, и есть решения данного простейшего тригонометрического уравнения.
Далее, при совершении бесконечного целого числа поворотов (2π) против часовой стрелки и по часовой стрелке, получим целую серию решений (множество значений х), при которых cosx будет равен 1/2, это значения х: π/3+2π; -π/3+2π; …
Все углы, соответствующие верхней точке на линии единичной окружности, описываются формулой: 
.
Аналогично, все углы, соответствующие нижней точке на линии окружности, описываются формулой: 
.
Обе серии решений можно описать одной формулой общего вида:
x = ±π/3 + 2πn, nϵZ
где n – число оборотов, выраженное положительным или отрицательным целым числом из множества целых чисел Z.
Остальные уравнения с косинусом решаются совершенно аналогично. Решение будем представлять лишь рисунком и ответом (формулой решения в общем виде).
2 
Рис.2
3. 
Рис.3
4. 
Рис.4
5. 
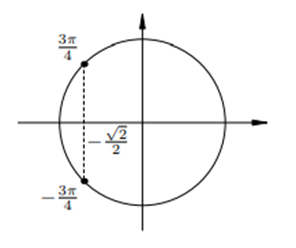Рис.5
6. 
Рис.6
Теперь рассмотрим уравнения с синусом. Тут ситуация немного сложнее.
7. 
Проведя горизонтальную линию, перпендикулярную оси синусов через заданное в уравнении значение sinx = ½, получим на единичной окружности горизонтальную пару точек с ординатой 1/2: это величины углов π/6 и 5π/6 радиан (Рис.7).
|
|
|
Эти две точки на единичной окружности, равные π/6 и 5π/6 радиан, и есть решения данного простейшего тригонометрического уравнения.
Далее, при совершении бесконечного целого числа поворотов (2π) против часовой стрелки и по часовой стрелке, получим целую серию решений (множество значений х), при которых sinx будет равен 1/2, это значения х: π/6+2π; 5π/6+2π; …
Рис.7
Все углы, соответствующие правой точке на линии единичной окружности, описываются формулой: 
.
Аналогично, все углы, соответствующие левой точке на линии окружности, описываются формулой: .
Можно оставить эти две записи решения в виде двух решений.
Тем не менее, объединяющая формула существует, и её надо знать!
где k – число оборотов, выраженное положительным или отрицательным целым числом из множества целых чисел Z.
На первый взгляд совершенно не ясно, каким образом она дает обе серии решений.
Но давайте посмотрим, что получается при чётных 
.
Если 
, то получим первую серию решений 
.
А если 
– нечетно, то есть 
,
то получим вторую серия решений – 
.
Обратим внимание, что в качестве множителя при 
обычно ставится правая точка, в данном случае 
.
Остальные уравнения с синусом решаются точно так же. Мы приведем рисунок, запись ответа в виде совокупности двух серий и объединяющую формулу.
8. 
Рис.8
9. 
Рис.9
10. 
Рис.10
х = (-1)k (-π/6)+πk, kϵZ
11. 
Рис.11
12. 
Рис.12
Переходим к решению табличной группы уравнений с тангенсом.
