Метод вариации произвольных постоянных (метод Лагранжа)

 

Пусть нам известно общее решение уравнения (7), т.е. . Тогда решение уравнения (6) будем искать в виде

.

Продифференцируем это равенство:

В силу произвольности выбора функци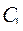й  и 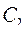  положим

                                     (10)

Тогда

Подставляя  в уравнение (6) и группируя члены, получаем

 (11)

Выражения в скобках в формуле (11) равны нулю, объединяя полученные результаты, приходим к системе

                                      (12)

из которой единственным образом находим  и , так как её опре-делитель является определителем Вронского . И тогда

Пример 4. Методом вариации произвольных постоянных найти общее решение уравнения

Найдём общее решение соответствующего однородного уравнения

Составим характеристическое уравнение 

Воспользуемся формулой (4) .

Здесь .

Составим систему (12)

Интегрируя последнее уравнение системы, находим , а из первого уравнения определяем

Окончательно получим общее решение

Ряды