Правильные и неправильные дедуктивные умозаключения

 

Ранее была разработана теория, позволяющая давать ответ на вопрос, является ли та или иная формула логическим следствием данной совокупности формул или нет, а также находить все логические следствия из данных формул. Применим ее к рассуждениям, представляющим собой последовательности высказываний (суждений), для того чтобы определить, правильно рассуждение или нет, т.е. правильное или неправильное умозаключение сделано с помощью данного рассуждения из данных посылок.

 

Пример 7.9. Рассмотрим следующее рассуждение: "Если четырехугольник 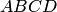— параллелограмм, то его противоположные углы равны. Четырехугольник 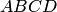— параллелограмм. Следовательно, его противоположные углы равны". Чтобы ответить на вопрос, верно ли это рассуждение, нужно выяснить, будет ли формула алгебры высказываний, отражающая структуру заключения данного рассуждения, логическим следствием формул алгебры высказываний, отражающих структуры его посылок. Структура посылок выражается формулами , а структура заключения — формулой . (Легко убедиться в этом, если вместо пропозициональной переменной подставить в формулы высказывание "Четырехугольник 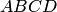— параллелограмм", а вместо — высказывание: "Противоположные углы четырехугольника 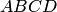равны".) Известно (см. правило 6.8), что формула является логическим следствием формул . Поэтому приведенное рассуждение является правильным, и сделанное заключение действительно следует из посылок.

 

Рассуждения такой формы нередки в математике. Приведем еще одно подобное рассуждение: "Если 10 делится на 3, то 100 делится на 3. 10 делится на 3. Следовательно, 100 делится на 3". Проведенное рассуждение правильно, но его заключение ложно. Это обстоятельство не должно нас смущать: ведь правильное рассуждение приводит к истинному утверждению при условии, что все посылки рассуждения были истинными. В данном случае из двух посылок одна не является истинной.

 

 

Пример 7.10. Рассмотрим следующее рассуждение: "Если курс математической логики неинтересен, то он полезен. Курс математической логики бесполезен или нетруден. Курс математической логики труден. Следовательно, этот курс интересен". Введем обозначения:

 

"Курс математической логики интересен";
"Курс математической логики полезен";
"Курс математической логики труден".

 

Тогда для ответа на вопрос, правильно ли приведенное рассуждение, нужно выяснить, справедливо ли следующее логическое следование:

 

 

Покажем, что оно справедливо. На основании равносильности из теоремы 4.4, у вторую посылку можно заменить на . Далее по правилу 6.14 имеем . Затем по правилу 6.13 . Последняя формула, на основании равносильности из теоремы 4.4, пункт а), равносильна формуле . Наконец, привлекая еще не использованную третью посылку , получаем на основании правила 6.8 . Учитывая свойство выводимости, установленное в теореме 6.5, пункт б), заключаем, что рассматриваемое логическое следование справедливо, и, таким образом, данное рассуждение правильно.

 

Обратим особое внимание на два типа наиболее часто встречающихся неправильных рассуждений. Первое рассуждение выглядит так. Мы исходим из некоторого предположения и, правильно рассуждая, приходим к правильному выводу. Отсюда делаем вывод, что сделанное предположение верно. С точки зрения математической логики схема этого рассуждения такова: из истинности утверждений и делается вывод об истинности утверждения . Чтобы ответить на вопрос о правильности такой схемы рассуждений, рассмотрим два примера рассуждений, основанных на этой схеме.

 

 

Пример 7.11. "Если число натуральное, то оно рациональное . Число 17 рациональное . Следовательно, число 17 натуральное ".

 

Пример 7.12. "Если число натуральное, то оно рациональное . Число рациональное . Следовательно, число натуральное ".

 

В каждом из этих рассуждений обе посылки являются истинными утверждениями. Но в первом случае мы приходим к истинному заключению (число 17 — натуральное), а во втором — к ложному (число не натуральное). Это означает, что неверной является сама схема построения умозаключения, примененная в этих примерах. Неверность, неправомочность схемы означает, что между посылками и заключением нет отношения логического следования. Здесь еще раз уместно подчеркнуть, что правильность умозаключения определяется формой умозаключения, а не истинностью входящих в него утверждений. Иначе говоря, анализируя правильность рассуждения, нужно помнить о том, что его правильность не совпадает с истинностью полученного заключения. Схема умозаключения — это и есть то, что изучает логика, а истинность утверждений, входящих в рассуждение, — это прерогатива той науки (или практики), откуда взяты эти утверждения. Развивая эту мысль, можно заметить, что и термин "следует" употребляется в разных смыслах. Важно понимать существенное различие между следованиями:

 

"из следует " и "из следует ".

 

Первое — утверждение логики, т.е. логическое следование, второе — как свойство отношения порядка в каком-то числовом множестве, есть некое математическое следование (т. е. следование в рамках некоторой математической теории). Мы придем к подробному рассмотрению этой связи в гл. 6 при уточнении понятия доказательства.

 

Итак, неправильность рассмотренной схемы рассуждений приводит к тому, что относительно исходного предположения нельзя сделать вывод о его истинности: оно может быть как истинным, так и неистинным, причем его истинность или ложность никак не связаны с проведенным рассуждением. Этот же вывод подтверждает математическая логика: логическое следование несправедливо, потому что формула не является тавтологией (проверьте!).

 

Тем не менее рассуждения по указанной схеме нередко встречаются в школьной практике, особенно в алгебре и тригонометрии. Так, при доказательстве тождества рассуждения начинаются именно с этого тождества: обе его части преобразуют так, что оно превращается в некоторое очевидное тождество. После этого делается заключение о том, что исходное тождество верно. Узнаете рассмотренную схему? Например, при доказательстве тригонометрического тождества

 

 

можно встретить такие рассуждения. "Умножим обе его части на . Получим:

 

Сгруппируем слагаемые в правой части:

 

Продолжим группировку в правой части:

 

 

Поделим обе части на . Получим: — известное тождество. Отсюда делается вывод, что исходное тождество доказано".

 

В данном случае правильным доказательством будет проведение рассуждений в обратном направлении, от известного (очевидного) тождества к исходному, данному тождеству. Эти рассуждения-преобразования здесь проделать можно и тем самым действительно доказать данное тождество. Но нередко умозаключение по такой неверной схеме приводит к ошибкам, т.е. к ложным утверждениям. Такие рассуждения иногда относят к разряду занимательной математики, где они получили название "парадоксов" или "софизмов".

 

 

Пример 7.13. Рассмотрим пример софизма. Докажем, что . Из чисел 3 и 7 вычтем одно и то же число 5. Получим: . Возведем числа -2 и 2 в квадрат. В результате получим равные числа: и . Следовательно, должны быть равны и исходные числа: .

 

Ясно, что полученное заключение ложно. Проанализируем проведенное рассуждение, чтобы обнаружить допущенную ошибку. Рассуждение состоит из трех шагов. Выделим эти шаги более отчетливо.

 

Первый шаг (вычитание из целых чисел 3 и 7 целого числа 5). Первая посылка "Если и — целые числа, то их разность а - b существует и есть число целое". Вторая посылка "Числа 3 и 5 (а также 7 и 5) — целые". Заключение "Разности и существуют, и ".

 

Данное умозаключение сделано по правилу modus ponens: и потому является правильным.

 

Второй шаг (возведение чисел –2 и 2 в квадрат). Первая посылка "Если число а целое, то его квадрат существует и является неотрицательным целым числом". Вторая посылка "Число –2 (а также число 2) — целое". Заключение "Квадраты чисел –2 и 2 существуют, причем и ".

 

Умозаключение и здесь сделано по правилу modus ponens: , и потому и на этом шаге рассуждения ошибка не допущена.

 

Третий шаг (заключение о равенстве чисел 3 и 7). Первая посылка "Если целые числа равны, то равны и их квадраты". Вторая посылка "Квадраты целых чисел –2 и 2 равны: ". Заключение "Равны сами числа –2 и 2, т. е. , т. е. ".

 

На данном этапе рассуждения умозаключение сделано по схеме: , которая не является правильной. Следовательно, в этом умозаключении сделана логическая ошибка, которая и привела к ложному выводу, несмотря на то что исходили мы из всех истинных посылок.

 

Второй распространенный тип неправильных рассуждений выглядит так. Мы исходим из некоторого неверного предположения и, правильно рассуждая, приходим к некоторому выводу. Отсюда делаем заключение, что полученный вывод неверен. С точки зрения математической логики схема этого рассуждения такова: из истинности утверждений и делается вывод об истинности утверждения . Следующие два примера рассуждений, основанных на этой схеме, позволяют ответить на вопрос о ее правомочности.

 

 

Пример 7.14. "Если число натуральное, то оно рациональное . Число не натуральное . Следовательно, число не рациональное ".

 

Пример 7.15. "Если число натуральное, то оно рациональное . Число не натуральное . Следовательно, число не рациональное ".

 

В каждом из этих рассуждений обе посылки являются истинными утверждениями. Но в первом случае мы приходим к ложному заключению (число — рациональное), а во втором — к истинному (число нерациональное). Это снова означает, что неверной является сама схема построения умозаключения, примененная в этих примерах, т. е. эта схема при всех истинных посылках не обязательно дает истинное следствие. Вывод, основанный на примерах, подтверждается математической логикой: из формул и не следует формула , в чем нетрудно убедиться, проверив, что формула не является тавтологией.

Складні силогізми.

Сложный силлогизм (полисиллогизм) – это сцепление ряда силлогизмов таким образом, что заключение одного становится посылкой другого силлогизма и т.д.. Всякое научное мышление в развернутой или скрытой форме представляет собой полисиллогизм, вытекающий из целой системы умозаключений.

Отличают особый вид сложного силлогизма – сорит, состоящий из сокращенных силлогизмов. В сорите приводится только последнее заключение, а все промежуточные опускаются. Общая формула сорита такова: А-В, В-С, С-Д, следовательно, А-Д. Видно, что здесь прослеживается стойкая цепь причин и следствий, от чего обоснованность вывода усиливается, он становится особенно убедительным.
Сложно-сокращенный силлогизм, в котором посылками служат энтимемы, называется эпихейрема. Схема эпихейремы такова:

М есть (не есть) Р, так как она есть (не есть) N,

S есть М, так как оно есть О

S есть (не есть) Р.

Например:

Ни одна птица не примат, так как ни одна птица не млекопитающее.

Данные особи – птицы, так как они имеют перьевой покров.

Данные особи не приматы.

Каждая эпихейрема может быть превращена в сорит, если ее посылки превратить в полные силлогизмы и расположить их определенным образом.