Временная характеристика детектора

Конечное время отклика детектора является причиной погрешностей (временной задержки, смещения и ошибок при определении присущих максимумам и минимумам значений) при анализе с разверткой частоты (рис. 4.19). Кроме того, временная характеристика детектора (в частности, детектора с интегратором в виде простой RС -схемы) ограничивает крутизну наклона поддающихся обработке спектров. Эти соответствующие результаты обработки проведены на рис. 4.20 и 4.21

Рис. 4.19. Систематические погрешности (временная задержка и погрешность определения присущих максимумам и минимумам значений) при анализе с разверткой частоты

Используя приведенные зависимости, представленные на рис. 4.19, можно оценить погрешности присущих максимумам и минимумам спектров значении при текущем линейном усреднении и при экспоненциальном усреднении с помощью простой RС-схемы.

Рис. 4.20. Погрешности определения присущих максимумам и минимумам спектров значений при текущем линейном и экспоненциальном (КС) усреднении

Приведенные зависимости на рис. 4.20 позволяют оценить соответствующие значения временной задержки, которые необходимо учитывать при разработке конверторов, использующих линейное или экспоненциальное усреднение. По показанным на рис. 4.21 кривым можно оценить временную задержку, относящуюся

Рис. 4.21. Временные задержки в процессе определения присущих максимумам и минимумам спектров значений при текущем линейном и экспоненциальном (RС) усреднении

к наклонным участкам получаемых в результате частотного анализа спектров. Отметим, что на рис. 4.21 также показан присущий усреднению с помощью простой RС -схемы асимптотический предел 8,7 дБ/2 RС, который соответствует максимальной скорости спада уровня отдаваемого детектором сигнала и на практике часто ограничивает скорость развертки частоты при анализе

Модуляция колебаний

Все сигналы во временной области были представлены суммами гармонических колебаний с фиксированными значениями амплитуды и частоты. По существу главная цель анализа Фурье заключается в выделении и определении этих фиксированных частот.

Модулированный сигнал часто наиболее удобно представить при помощи одного колебания с изменяющимися во времени амплитудой и «мгновенной частотой» [8, 10, 24]. Разумеется, что при представлении модулированного сигнала также можно использовать пару комплексно сопряженных колебаний. Однако более удобно использовать одну частоту и его проекцию на действительную ось.

Общий модулированный сигнал можно описать выражением

,                        (4.15)

в котором амплитуда A(t) и мгновенный фазовый угол   являются функциями времени. Мгновенная частота дается выражением   (рад/с) или  (Гц). Отметим, что в случае, если   содержит только составляющие с положительными значениями частоты, то речь идет об аналитическом сигнале.

Рассмотрим в качестве примера амплитудно-модулированный сигнал, который описан выражением:

                                       (4.16)

в котором частота f₀ является фиксированной несущей частотой, а функция A (t) является модулирующей функцией, соответствующей огибающей модулированного сигнала (обычно с определенным смещением постоянного тока). На рис. 4.22 показана составляющая с несущей частотой g_c (t)во временной области и ее спектр G_c (f)в частотной области, модулирующий сигнал g_М (t)с составляющей постоянного тока во временной области и соответствующий спектр G _М (f) в частотной области и модулированный сигнал g_c (t)^. G_М (t)во временной области и определенный на основе теоремы свертки спектр G_c (f)^. G_М (f)последнего. Спектр амплитудно-модулированного сигнала имеет боковые полосы, расположенные на соответствующем частоте модулирующего сигнала f_m расстоянии вокруг несущей частоты f_c. Отметим, что показанные на рис. 4.22 сигналы являются косинусоидальными волнами, способствующими более наглядному графическому представлению. Однако в общем случае справедливо, что фазовые соотношения обеих боковых полос таковы, что их векторная сумма всегда совпадает с фазором

Рис. 4.22. Спектр амплитудно-модулированного сигнала

 

составляющей с несущей частотой. На рис. 4.23 показан аналитический сигнал, соответствующий показанному на рис. 4.22 амплитудно-модулированному сигналу.

 

Рис. 4.23. Амплитудная модуляция, представленная векторной суммой трех колебаний

 

Этот аналитический сигнал можно рассматривать как один вращающийся фазор, амплитуда которого изменяется по синусоидальному закону между двумя пределами. Путем анализа Фурье можно колебание с изменяющейся амплитудой разложить на три колебания с фиксированными амплитудами. Эти колебания показаны на рис. 4.23.

Процесс разложения более сложен в случае фазовой или частотной модуляции. Однако представление при помощи аналитического сигнала относительно просто даже в этих случаях. Аналитический сигнал, представляющий частотно-модулированный сигнал, созданный путем модуляции, имеющей неизменную амплитуду составляющей с несущей частотой модулирующим сигналом с единой частотой, показан на рис. 4.23.

Математическое выражение, описывающее аналитический сигнал, имеет вид

 

                               (4.17)

 

Символом β обозначено максимальное отклонение фазы (в радианах) от линейно увеличивающегося фазового угла составляющей с несущей частотой f₀. Фазовую модуляцию с единой модулирующей частотой можно также рассматривать как частотную модуляцию с единой модулирующей частотой. Мгновенный фазовый угол аналитического сигнала дается выражением

                            ( 4.18)

Выражение, определяющее мгновенную частоту, получается путем дифференцирования выражения (4.17), т.е.

                (4.19)

Следовательно, максимальное отклонение частоты ∆f равно β, причем β = ∆f/f_М называется «коэффициентом модуляции». Рис. 2.22 иллюстрирует как мгновенные фазу и частоту, так и β и ∆f.

Представление модулированного по фазе аналитического сигнала в виде суммы колебаний с фиксированной частотой относительно затруднительно и предъявляет требования к применению функций Бесселя. На рис. 4.22 показаны примеры (односторонних) спектров амплитуды модулированных сигналов с различными значениями коэффициента β. модуляции β. Можно доказать, что относительные амплитуды составляющей с несущей частотой и боковых полос n-го порядка равны соответственно J₀(β) и J_n (β), причем символом J_n (β) обозначена Бесселева функция 1-го рода с индексом п и аргументом

На  рис. 4.25 видно, что в случае β < 1 почти вся важная информация сосредоточена в первых двух парах боковых полос, причем при β << 1 достаточна лишь одна пара боковых полос. Эти два случая целесообразно рассмотреть более подробно, так как на их основе можно понять взаимосвязь с амплитудной модуляцией.

Рис. 4.25 иллюстрирует показанный на рис. 4.23 процесс амплитудной модуляции в системе координат, вращающейся с частотой составляющей несущей частоте f₀ (т.е. умноженой на   или вычитаемой из частоты f₀ частот всех составляющих спектра). Результат векторного сложения присущих верхней и нижней боковым полосам несущего сигнала совпадает с частотой модуляции, составляющей несущей частоте. В случае, если фаза присущего одной боковой полосе частоты модуляции опрокинута (см. рис. 4.26), то результатом векторного сложения является модуляция  с изменяющейся по синусоидальному закону амплитудой, направленной перпендикулярно к частоте модуляции, составляющей с несущей частотой угол сдвига по фазе. Окончательный результат векторного сложения упомянутых элементов модуляции (гипотенуза) будет колебание с почти неизменной амплитудой, но с фазой, изменяющейся по синусоидальному закону относительно составляющей с несущей частотой. Такая модель фазовой модуляции с одной парой боковых полос приемлема только в случае малых отклонений фазы, т.е. при β << 1.

Рис. 4.25.  Примеры спектров амплитуды модулированных по частоте сигналов с различными значениями коэффициента модуляции β

Рис 4.26.  Фазовые соотношения боковых полос при амплитудной и фазовой модуляции

При увеличении значений β необходимо учесть боковые полосы более высокого порядка с тем, чтобы компенсировать изменения длины упомянутой выше гипотенузы. Это показано на рис. 4.27, в котором при β = 1 рад использовались действительные значения Бесселевых функций J ₀(β), J ₁(β) и J₂ (β) для графического создания результирующей формы колебаний с учетом боковых полос до второго порядка.  

В интервале времени, соответствующем одной четвертой оборота боковых полос первого порядка (длина J₁(β)), боковые полосы второго порядка (длина J₂(β)) поворачиваются на половину оборота.  и     представляют длину результата (с учетом двух пар боковых полос) при равном соответственно 0, 45 и 90° угловом смещении боковых полос первого порядка. Легко видеть, что длины  и  соответствуют длинам сегментам окружности, получаемых на основе всех боковых полос с неизменной амплитудой. Рассмотренный выше пример, вероятно, дает представление о взаимодействии боковых полос при несложной амплитудной или фазовой модуляции в более общих случаях модуляции.

Несмотря на то, что характерным для этих простых видов модуляции является симметричное расположение боковых полос, фазовые соотношения снизу и сверху несущей частоты отличаются друг от друга и обусловливают усиление с одной стороны и ослабление (или даже аннулирование) с противоположной стороны последней. Очевидно, что применение аналитических сигналов при моделировании модулированных по амплитуде или фазе сигналов ограничено и практически допустимо лишь там, где обусловленные модуляцией боковые полосы не перекрывают равную нулю частоту (см. рис. 4.28). Следовательно, в случае амплитудной модуляции несущая частота должна превышать самую высокую модулирующую частоту. В случае частотной модуляции несущая частота должна превышать как 4f_m, так и 2 ∆f (см. рис. 4.18), где f_m - самая высокая модулирующая частота и ∆f- максимальное отклонение частоты, соответствующее максимальной амплитуде модулирующего сигнала.

 

Рис. 4.27. Иллюстрация происходящей за счет боковых полос второго порядка компенсации изменяющейся длины гипотенузы

В случае комбинированной амплитудной и частотной (или фазовой) модуляции боковая полоса с самой низкой частотой модулированной по фазе составляющей ()должна превышать самую высокую частоту модулирующего по амплитуде сигнала (A (t)).

Рис 4.28. Ограничение ширины боковых полос единой составляющей с несущей частотой

К более сложным видам колебаний относятся модулированные колеба­тельные процессы

s (t) = A (t)(s in(ω (t) t + φ(t)) = A (t) cosψ(t) ,             ( 4.20)

у которых один либо несколько параметров изменяются во времени. В зави­симости от того, какой из трех параметров периодически изменяется, разли­чают амплитудно-модулированные (АМ), частотно-модулированные (ЧМ) и модулированные по фазе (ФМ) периодические колебания. В большинстве случаев эти параметры изменяются настолько медленно, что в пределах од­ного периода колебательный процесс можно считать гармоническим.

Во время работы в результате соударения деталей в механизме возбуж­даются колебания на собственных частотах. Эти частоты являются констан­тами механизма и не меняются при изменении его состояния. Поэтому само синусоидальное колебание на собственной частоте не несет диагностической информации. Выделение одной из собственных частот ω₀, называемой несу­щей, позволяет оценить структуру колебания на этой частоте. Это колебание можно записать в следующем виде

s (t) = A (t) s in(ω₀ t + φ (t)),                           (4.21)

 

т.е. амплитуда и фаза этого гармонического колебания меняются со временем по определенному закону. Изменения амплитуды связаны с тем, что в мо­мент удара в материал механизма передается определенная порция энергии и амплитуда упругих колебаний скачком увеличивается до значения A. Затем энергия колебаний постепенно рассеивается и их амплитуда уменьшается по экспоненциальному закону . К моменту очередного удара амплитуда ко­лебаний уменьшается до A , после чего материал снова получает порцию энергии. Изменение амплитуды называют модуляцией, а разность между наибольшим и наименьшим значениями амплитуды, отнесенную к наиболь­шей амплитуде, называют глубиной модуляции и обозначают

.                                      ( 4.22)

 

Глубина модуляции зависит от периода следования ударов T и вели­чины коэффициента затухания d. Функция A(t), соответствующая изме­нению амплитуды синусоидального колебания, называется огибающей сигнала. Ее параметры зависят от интенсивности соударения деталей, часто­ты следования и фазы импульсов. В момент соударения деталей меняется не только амплитуда, но и фаза колебаний. Согласно высказанным выше сооб­ражениям, изменение амплитуды носит пилообразный характер. Но прежде чем рассмотреть этот случай, положим, что амплитуда синусоиды sin(ω ₀ t) меняется также по синусоидальному закону, но со значительно меньшей час­тотой, чем ω ₀. И так:

 

                                 (4.23)

причем ω₀ >>Ω, \ R \< 1.

Раскрывая скобки, получим

                   (4.24)       

 

 

Амплитудно-модулированный (АМ) сигнал (Рис. 4.29, б) в отличие от весьма похожих по виду биений (Рис. 4.29, а) состоит из трех гармонических составляющих, одна из которых имеет частоту несущей ω ₀, а две другие называют боковыми: (ω ₀ – Ω) и (ω ₀ + Ω).

 

        

Рис. 4.29. Биения (а) и амплитудная модуляция (б)

 

По виду временной реализации виброакустического сигнала часто трудно отличить биения от модуляции при условии что частота модуляционного сигнала существенно выше (в несколько раз) несущего сигнала, и только спектральный анализ позволяет однозначно оценить характер сигнала. На рис. 4.30 в качестве примера приведен результат записи временного сигнала с экрана прибора при соотношении частоты несущего сигнала к частоте модуляционного ω _о / ω _m = 16. Спектральная характеристика данного сигнала (с экрана прибора) приведена на рис 4.31. Спектр модулированного колебания будет иметь спектральную линию на частоте несущей ω ₀ и, симметрично расположенные по отношению к ней модулирующую частоту ω_m.

 

Рис. 4.30. Временная реализация амплитудно-модулированного сигнала

Рис. 4. 31. Амплитудно-модулированный вибросигнал

 

В более сложном случае, когда амплитуда меняется по произвольному закону A (t), эту функцию можно разложить на гармонические составляющие и рассмотреть модуляцию каждой составляющей в отдельности.

Примером частотно-модулированного (ЧМ) колебания является про­цесс вида

 

                      (4.25)

 

где Δω – величина частотного отклонения, называемая девиацией частоты или просто девиацией; Ω - частота гармонической модуляции.

Амплитуда такого процесса не меняется во времени, а частота изменя­ется по гармоническому закону относительно некоторой несущей частоты ω ₀. Спектр ЧМ колебания значительно сложнее, чем спектр АМ колебания. При очень малых девиациях (Δω/Ω<< 1)спектр содержит одну центральную и две боковые линии (ω₀ – Ω), (ω₀ + Ω), имеет ширину 2Ω. При возрастании девиации частот (Δω/Ω = 0,5... 1) приобретает некоторую значимость вторая пара боковых частот, поэтому ширина спектра возрастает до 4Ω.

При увеличении девиации спектр будет включать все новые значимые пары кратных частот. При (Δω/ Ω» 1) ширина спектра ЧМ колебания близ­ка к удвоенной девиации частоты 2D ω, а число линий в спектре будет столь велико, что он может быть ошибочно принят за непрерывный спектр.

Модулированные по фазе колебания тесно связаны с частотно-модулированными колебаниями, поскольку угловая частота есть не что иное, как скорость изменения фазы колебания (  ), то фаза колебаний определится

                                           (4.26)

 

В случае гармонической модулирующей функции по виду колебатель­ного процесса и по его спектру нельзя заключить, с какой модуляцией имеем дело с частотной или фазовой. Различие между ними проявится лишь в ре­зультате изменения частоты модуляции.

При частотной модуляции величина девиации Δω не изменится, а при фазовой модуляции изменение Δφ будет прямо пропорционально изменению частоты модуляции Ω. В действитель­ности исследуемые колебательные процессы часто являются модулирован­ными одновременно как по амплитуде, так и по частоте (фазе). При этом обычно нарушается симметрия спектра, но отличить один вид сложной мо­дуляции от другого при помощи анализа спектров весьма трудно, а часто и невозможно.

Современные методы теории аналитического сигнала [16] позволяют выделить (демодулировать) из колебательного процесса его мгновенную ам­плитуду (огибающую) A (t), мгновенную фазу φ (t)и мгновенную частоту ω (t). Для получения этих мгновенных функций необходимо с помощью ин­тегрального преобразования Гильберта преобразовать исходный процесс x (t), заданный на интервале Т₁ < t < Т₂, в сопряженный процесс     [16]:

                                                  (4.27)

где интеграл понимается в смысле главного значения.

Преобразование Гильберта можно осуществить, например, если на вход фильтра с импульсной характеристикой подать сигнал, определяемый функцией x(t), [16]:   

                                          (4.28)

 

где знаком * обозначена свертка функций  и x(t).

Физический смысл интегрального преобразования Гильберта для сигнала, представленного в частотной области, заключается в фазовом сдвиге всех спектральных составляющих исходного сигнала на π/2. Двойное преобразование Гильберта приводит к исходному процессу, но только с обратным знаком, т.е. осуществляет сдвиг исходного сигнала на π.

Используя понятие аналитического сигнала

 

                                           (4.29)

 

можно однозначно определить мгновенные амплитуду (огибающую),  фазу и частоту процесса [16, 27]:

 

; ;      (4.30)

 

Спектральный анализ

 

Спектральный анализ – один из методов обработки сигналов, который позволяет охарактеризовать частотный состав измеряемого сигнала. Преоб­разование Фурье является математической основой, которая связывает вре­менной сигнал (или же некоторую модель этого сигнала) с его представлени­ем в частотной области. Важную роль в спектральном анализе играют мето­ды статистики, поскольку виброакустические сигналы, как правило, пред­ставляют собой смесь шумовых и периодических составляющих [10, 24]. Поэтому по отрезку сигнала можно получить только оценку его спектра.

В основе преобразования Фурье (ПФ) лежит чрезвычайно простая, но исключительно плодотворная идея – почти любую периодическую функцию можно представить суммой отдельных гармонических составляющих (сину­соид и косинусоид с различными амплитудами A, периодами T (частотами ω))(см. рис. 4.32). Нижняя часть рисунка есть иллюстрация од­ного из основных принципов ПФ – спектр суммарной функции времени ра­вен сумме спектров ее гармонических составляющих.

Если s (t)– периодическая функция с периодом T, так что s (t) = s (t+T), а также являющаяся непрерывной на этом интервале или имеющая конечное число разрывов первого рода (т.е. функция s(t) должна иметь конечные пределы) и имеющая на интервале T конечное число макси­мумов и минимумов, то ее можно представить бесконечной суммой тригоно­метрических функций

                                           (4.31)

  где      T – длительность сигнала; ω_k = ω ₁ k,     k =1, 2, 3,....; коэффициенты a_k и b_k являются скалярны­ми произведениями функции s (t) на функции cos ω_kt и sin ω_kt, т.е. служат проекциями вектора s (t) на координатные оси, ортами которых служат ука­занные тригонометрические функции.

Любую гармонику ряда Фурье можно представить в виде амплитуды c_k (модуля) и начальной фазы φ_k (аргумент). Для этого коэффициенты ряда следует записать в виде a_k = c_k cosφ_k, и  b_k = c_k s in φ_k,, так что

 и , .                         (4.32)

 

Тогда соотношение (4.31) можно записать в другом виде:

,                                            (4.33)

где φ_k –  начальная фаза; k -й гармоники сигнала; c_k - ее амплитуда.

Совокупность чисел c_k называют амплитудным спектром, а числа φ_k – спектром его фаз. Из приведенных соотношений видно, что в общем слу­чае периодический сигнал содержит не зависящую от времени постоянную составляющую s₀ и бесконечный набор гармонических колебаний, так назы­ваемых гармоник с частотами    k = 1,2,3,..., кратными основной частоте.

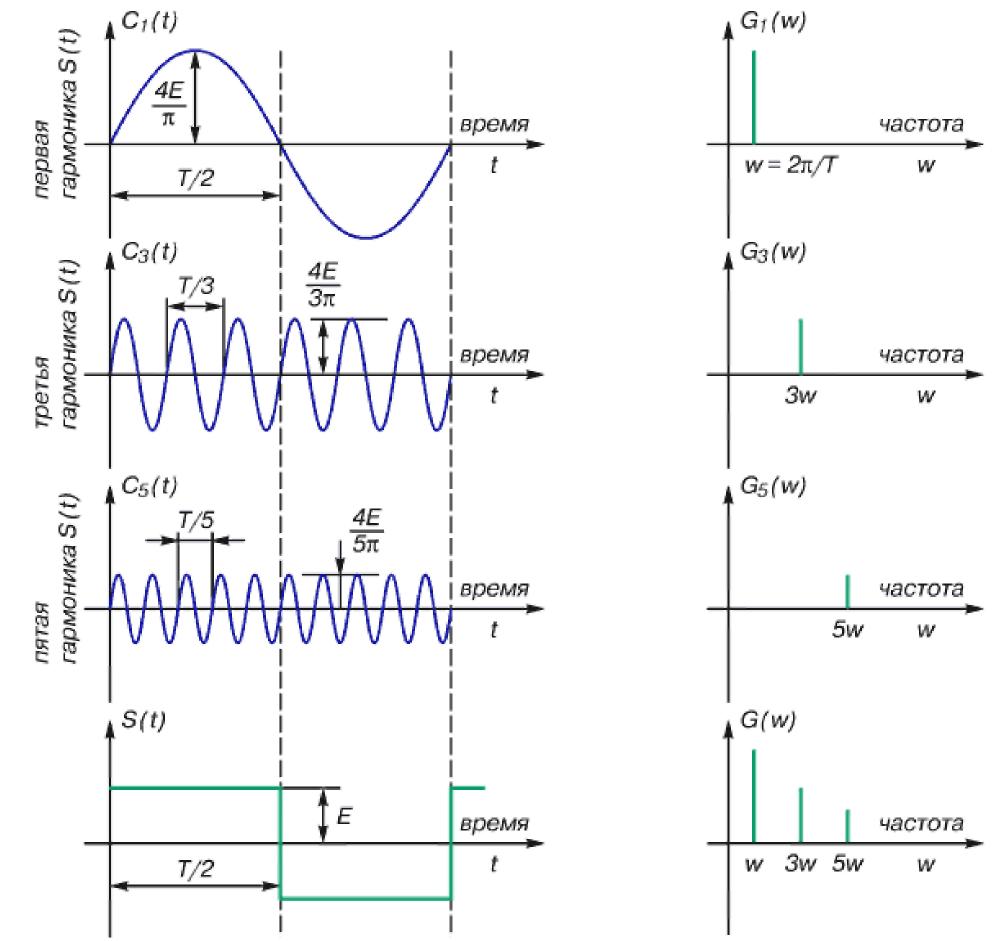
Рис. 4.32. Представление прямоугольного импульса суммой гармонических составляющих

 

 

Применив формулы Эйлера в ряд (4.32) можно представить в экспо­ненциальном виде

 

                                             (4.34)                                 

или

.                                           (4.35)

Комплексный спектр C_k можно выразить и с помощью интеграла

                                               (4.36)

где C_k = (a_k -ib_k)/ 2 = c_ke^-φk/2, C_-k = (a_k + ib_k)/ 2 = c_ke ^+iφk / 2 ,c_k= 2| C_k |, c ₀ = C ₀.

 

Спектр является важнейшей характеристикой сигнала и отражает все его свойства. Зная спектр можно восстановить сигнал. В этом смысле пред­ставления сигнала в виде функции времени и в форме спектра (в виде функ­ции частоты) равнозначны. Но для решения конкретной задачи бывает удоб­нее то или другое представление сигнала, поэтому рассматривают его в двух аспектах: во временном и спектральном.

Говоря о равнозначности спектра и временной формы сигнала, подра­зумевают комплексный спектр, т.е. спектр амплитуд и фаз. На практике, говоря о спектре, чаще всего имеют в виду спектр амплитуд. По спектру ам­плитуд нельзя восстановить первоначальную форму сигнала, однако ампли­тудный спектр обычно вскрывает такие свойства сигнала, ради которых и прибегают к спектральному представлению.

Следует отметить, что формулы (4.33), (4.34) и (4.36) справедливы только для периодических сигналов. Но это ограничение несущественно (и это можно доказать в достаточно строгой форме). Поскольку любой сигнал s (t) существует на конечном интервале времени 0 ≤t≤T и интересует его форма только на этом интервале, то ничто не мешает считать его периодиче­ским вне указанного интервала. Можно предположить, что

s (t) = s (t + T) .                                                       (4.37)

Интервал (0, T), на котором задан сигнал, рассматривается как один из его периодов, вне которого форма сигнала повторяется. Но возможен и дру­гой подход, при котором считается, что до момента времени t = 0 сигнала не было, вернее он был равен нулю, а также и после момента t = T он стал равен нулю. При таких предположениях суммы в формулах (4.31) и (4.34) следует заменить интегралами. Ряд (4.35) переходит в интеграл

                                         (4.38)

а формула (4.32), выражающая спектр сигнала, принимает вид

                                              (4.39)

В общем случае, когда не уточнено значение T, спектральная плот­ность записывается в виде

                                                     (4.40)

Соотношения (3.22) и (3.23) являются соответственно прямым и обрат­ным преобразованием Фурье .  Функция S(ω) называется спектральной плотностью. Ее модуль | S (ω) | характеризует распределение интенсивности гармонических составляющих сигнала s (t)по частотам.

 

Кепстральный анализ

При применении методов, относящихся к определению кепстров, учитываются функции, которые можно рассматривать как «спектры логарифмических спектров». По существу понятие кепстра было введено уже в 1963 г. в связи с дефиницией кепстра мощности как «спектра мощности логарифмического спектра мощности» [10, 24]. Кепстр мощности был предложен в качестве более эффективной альтернативы автокорреляционной функции при обнаружении эха в сейсмических сигналах. Поскольку соответствующая функция по определению отображала спектр спектра, авторы работы [7, 10] воспользовались терминологической аналогией и согласно термину «спектр» придали этой функции название «кепстр». Аналогичным образом возникли и термины «квефренция» (quefrency), «рагмоника» (rahmonic), «лифтр» (lifter), «гамнитуда» (gamnitude) и «сафе» (saphe), основанные на аналогии с английскими терминами для частоты (frequency), гармоники (harmonic), фильтра (filter), модуля (magnitude) и фазы (phase). Термины кепстр, квефренция и рагмоника нашли широкое применение и используются в даннм разделе. Относительно часто используются и термины, относящиеся к лифтру (лифтрация, пролифтрованный и т.п.) и указывающие на процесс фильтрации в кепстральной области. Отметим, что упомянутые выше термины приняты фирмой Брюль и Кьер и учтены как в конструкции двухканальных анализаторов сигналов 2032 и 2034, так и в соответствующей технической литературе.

Однако самая важная особенность кепстра заключается не в том, что он представляет спектр спектра, а в логарифмическом преобразовании исходного и подвергаемого дальнейшей обработке спектра. Отметим, что автокорреляционную функцию, определяемую на основе собственного спектра мощности путем обратного преобразования Фурье, также можно рассматривать как «спектр спектра». По существу, используемая в настоящее время дефиниция кепстра определяет кепстр мощности как «обратную трансформанту Фурье логарифмического спектра мощности». Различие между этой дефиницией и дефиницией автокорреляционной функции заключается лишь в логарифмическом преобразовании исходного спектра.

 Рис. 4.33 иллюстрирует ситуацию, в которой кепстр более эффективен, чем автокорреляционная функция. На рис. 4.33 a показан определенный спектр мощности в логарифмическом и линейном масштабе (разумеется, что линейная шкала амплитуды проградуирована в единицах возведенной в квадрат амплитуды). Рис. 4.33 6 и 4.33 b показывают результаты обратного преобразования Фурье, т.е. соответственно автокорреляционную функцию и кепстр. В представленном в логарифмическом масштабе спектре на рис. 4.33 а видны серии гармоник (обусловленные дефектом шарикоподшипника гармоники). Присутствие этих серий гармоник легко обнаружить по кепстру на рис. 4.33 b, содержащему соответствующие рагмоники (отдельные рагмоники обозначены символами 1, 2и т.д.). Соответствующую информацию весьма трудно получить на основе показанной на рис. 4.33 6 автокорреляционной функции, форма кривой которой почти совершенно определена двумя наибольшими пиками исходного спектра, т.е пиками, преобладающими при представлении этого спектра в линейном масштабе.

Кепстр, определенный на основе спектра мощности, в настоящее время называется «кепстром мощности». Другим видом кепстра является введенный недавно «комплексный кепстр» [7]. Так как комплексный кепстр определяется на основе комплексного спектра, в нем учтена информация как о логарифме

Рис. 4.33. Спектр мощности в линейном и логарифмическом масштабе, автокорреляционная функция и кепстр практического сигнала

амплитуды, так и о фазовом угле. Следовательно, комплексный кепстр можно преобразовать назад в исходный сигнал во временной области, в то время как кепстр мощности допускает обратное преобразование в спектр мощности. Отметим, что исходная дефиниция кепстра исключала возможность его обратного преобразования. Обработка кепстров, в частности модифицирование (редактирование) комплексных кепстров, является примером «гомоморфной» обработки сигналов. Соответствующая широкая область более подробно рассмотрена в специальной литературе [7].