Преобразование Лапласа

Для вычисления выхода системы при известном входе необходимо решение дифференциального уравнения. Чтобы упростить процедуру, математики ввели преобразование, позволяющее заменить решение дифференциальных уравнений алгебраическими вычислениями, то есть, операциями с полиномами (многочленами) и рациональными функциями. Для непрерывной функции времени , которая определена только для положительного времени (t > 0) вводится преобразование Лапласа, которое обозначается как : (12)

(12)

Функция называется изображением для функции (оригинала). Здесь - это комплексная переменная, которая выбирается так, чтобы интеграл (12) сходился. Суть в том, что функция вещественных переменных заменяется ее изображением, связь между которыми осуществляется через оператор Лапласа. Такая замена позволяет свести решение дифференциальных уравнений к простейшим алгебраическим операциям для нахождения изображения. А зная изображение, можно найти искомую функцию по специальным формулам.

Обратное преобразование Лапласа позволяет вычислить оригинал по известному изображению : (13)

(13)

где , постоянная, а выбирается так, чтобы интеграл сходился. Постоянная должна быть больше, чем показатель роста функции-оригинала .

На практике вместо интеграла (12) чаще всего используют готовые таблицы, по которым можно сразу определить изображение по оригиналу и наоборот. Например, изображения по Лапласу для дельта-функции, единичного скачка и функции равны, соответственно (14)

, , (14)

СЛАЙД 20.

Передаточная функция

СЛАЙД 21. В теории автоматического управления используются различные преобразования обыкновенных дифференциальных уравнений. Модель объекта задана линейным дифференциальным уравнением второго порядка, связывающим вход 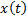и выход 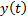: (15)

(15)

где 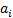(i = 0,1) и (i =0,1,2) - постоянные.

Производные сигналов и по времени в операторной форме: ,

Подставляя эти выражения в (15), получим (16):

. (16)

Можно формально вынести за скобки 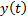в левой части равенства и 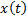в правой части (17):

(17)

Левая часть (20) означает, что в правой части оператор действует на сигнал 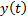, а в правой части оператор действует на сигнал 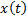. Разделив обе части на оператор , связь выхода и входа можно записать в виде (18):

(18)

Где запись означает не умножение, а действие сложного оператора (19)

(19)

на сигнал 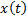. Иначе говоря, формула — это не что иное, как удобная использования символическая запись уравнения (19).

Функция называется передаточной функцией объекта, который описывается уравнением (18). Она полностью описывает связи между выходом и входом объекта при нулевых начальных условиях, но не учитывает его внутреннее устройство. Т. о. передаточная функция – это отношение операторов правой и левой частей дифференциального уравнения. Знаменатель передаточной функции определяет характеристическое уравнение для исходного уравнения, с помощью которого описывают свободные движения (например, колебания) системы (20)

(20)

– характеристический полином. Его корни, , называются полюсами, а корни полинома числителя передаточной функции, , называются нулями системы.

Строго говоря, есть две формы записи:

• операторная запись, когда передаточная функция записывается как функция оператора дифференцирования 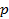, входы и выходы блоков - функции времени;

• запись в изображениях, когда передаточная функция записывается как функция комплексной переменной , а для обозначения входов и выходов используют их изображения по Лапласу.

Однако суть дела от этого не меняется. Поэтому дальше при обозначении сигналов мы, несколько жертвуя строгостью ради простоты записи, будем обозначать сигналы строчными буквами, не указывая независимую переменную (), а в записи передаточных функций будем использовать переменную p, как принято в литературе.

СЛАЙД 22. Зависимость между характеристиками звена:

1. Связь между переходной функцией и функцией веса :

2. Связь между функцией веса и передаточной функцией определяется через преобразование Лапласа:

3. Связь между передаточной функцией и переходной функцией определяется через преобразование Лапласа:

4. Выход системы 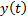вычисляется как интеграл для произвольного входного сигнала 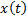при нулевых начальных условиях

или

Пример

СЛАЙД 23. Рассмотрим пример использования преобразования Лапласа для вычисления выхода системы при известном входном сигнале. Пусть объект управления описывается уравнением первого порядка (21):

, (21)

и на его вход поступает единичный ступенчатый сигнал . Требуется найти сигнал выхода 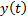, который в данном случае представляет собой переходную характеристику.

Решим эту задачу с помощью передаточных функций и изображений сигналов по Лапласу. Чтобы найти изображение выхода по формуле, нужно знать изображение входного сигнала и передаточную функцию звена . Изображение входа находим по табличным данным (см. (14)), а передаточную функцию - из (21), повторяя приведенные выше рассуждения: .