Реальные объекты не могут мгновенно изменять свое состояние, поэтому вместо статических моделей для их исследования используют динамические модели, которые описываются дифференциальными уравнениями, содержащими производные (скорости изменения сигналов). Во многих случаях точные модели представляют собой нелинейные дифференциальные уравнения, поэтому для того, чтобы применить теорию линейных систем, опять требуется линеаризация. При этом применяется почти та же методика, что и для алгебраических уравнений.
Под линеаризацией понимается замена нелинейных дифференциальных уравнений линейными уравнениями, которые с достаточной для практики точностью описывают физические процессы в САУ. Признаком, позволяющим произвести линеаризацию уравнений с математической точки зрения, является отсутствие разрывных, неоднозначных или резко изменяющихся характеристик, определяющих зависимость переменных уравнений от различных факторов, т.е. существование производных функций по всем переменным. Физической предпосылкой линеаризации является малая величина отклонений переменных в уравнениях элементов от их установившихся значений в силу самого принципа работы замкнутой автоматической системы, в состав которой эти элементы входят. Сущность линеаризации в том, что все нелинейные функции одной или нескольких переменных, входящих в уравнение элемента, разлагают в ряд Тейлора в окрестности точки, соответствующей установившемуся режиму, по степеням отклонений.
|
|
|
Так, формула Тейлора для некоторой нелинейной функции  двух переменных x и y в окрестности точки
двух переменных x и y в окрестности точки  имеет следующий вид (9):
имеет следующий вид (9):
 (9)
(9)
где  - установившиеся значения переменных;
- установившиеся значения переменных;  - отклонения переменных от
- отклонения переменных от  ;
;  - текущие значения переменных;
- текущие значения переменных;  - остаточный член.
- остаточный член.  и
и  - частные производные функции
- частные производные функции  по
по 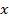 и
и  в точке
в точке  .
.
Индекс «0» соответствует условию  .
.
В формуле все частные производные вычисляются в точках с координатами  и
и  и поэтому являются постоянными величинами. Принимают допущение о малой величине, ограничиваются членами первого порядка малости, т.е. пренебрегают остаточным членом ряда. Тогда с точностью до членов второго порядка малости получим формулу Тейлора в виде (10)
и поэтому являются постоянными величинами. Принимают допущение о малой величине, ограничиваются членами первого порядка малости, т.е. пренебрегают остаточным членом ряда. Тогда с точностью до членов второго порядка малости получим формулу Тейлора в виде (10)
 . (10)
. (10)
В итоге получим линеаризованные уравнения в отклонениях, которые являются линейными дифференциальными уравнениями с постоянными коэффициентами и используются для исследования динамических свойств элементов. Неизвестными теперь будут не сами искомые переменные, а их отклонения от установившихся значений. 
СЛАЙД 10. Модель бака с водой не учитывает, изменение уровня по мере вытекания воды. Если для поддержания уровня используется насос, который подкачивает воду в бак для такого объекта входом является расход этого насоса  , а выходом - изменение уровня
, а выходом - изменение уровня  .
.
|
|
|
В течение малого интервала  расходы
расходы  и
и  можно считать постоянным. За это время объем воды, добавленной в бак насосом, равен
можно считать постоянным. За это время объем воды, добавленной в бак насосом, равен  , а объем вытекшей воды -
, а объем вытекшей воды -  . Учитывая, что площадь сечения бака равна
. Учитывая, что площадь сечения бака равна  , получаем изменение уровня (11):
, получаем изменение уровня (11):
 . (11)
. (11)
Переходя к пределу при  , получаем дифференциальное уравнение (12):
, получаем дифференциальное уравнение (12):
 (12)
(12)
Модель учитывает, что уровень воды и расход изменяются во времени. Расход вытекающей жидкости  зависит от уровня воды в баке
зависит от уровня воды в баке  и связан с ним нелинейной зависимостью(1)
и связан с ним нелинейной зависимостью(1)  . Поэтому уравнение можно записать в виде (13)
. Поэтому уравнение можно записать в виде (13)
 (13)
(13)
Здесь остались только две изменяющиеся величины: расход насоса  (вход объекта) и уровень воды
(вход объекта) и уровень воды  (выход). Далее для упрощения записи мы не будем явно указывать зависимость этих сигналов от времени.
(выход). Далее для упрощения записи мы не будем явно указывать зависимость этих сигналов от времени.
В установившемся (статическом) режиме, когда сигналы не изменяются, все производные равны нулю. В нашем случае, приняв  , получаем (14):
, получаем (14):
 (14)
(14)
Эта зависимость между установившимися значениями входа  и выхода
и выхода  называется статической характеристикой. Она позволяет для любого заданного постоянного значения
называется статической характеристикой. Она позволяет для любого заданного постоянного значения  на входе получить значение выхода
на входе получить значение выхода  .
.
Теперь предположим, что задана некоторая рабочая точка, то есть, значения входа  и выхода
и выхода  удовлетворяют уравнению (5), и система все время работает около этого положения равновесия. Вблизи этой точки:
удовлетворяют уравнению (5), и система все время работает около этого положения равновесия. Вблизи этой точки:  ,
,  , где
, где  и
и  - малые отклонения входа и выхода от рабочей точки.
- малые отклонения входа и выхода от рабочей точки.
В роли 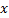 выступает расход
выступает расход  , а в роли
, а в роли 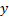 - уровень
- уровень  . Дальше для линеаризации используется разложение функций в ряд Тейлора и дифференцируем (15):
. Дальше для линеаризации используется разложение функций в ряд Тейлора и дифференцируем (15):

 . (15)
. (15)
Тогда (16):
 . (16)
. (16)
Тогда подставив  ,
,  в уравнение (4) и учитывая (17)
в уравнение (4) и учитывая (17)
 (17)
(17)
Получим (18):
 (18)
(18)
СЛАЙД 11.  и
и  соответствуют статическому режиму, то есть (19)
соответствуют статическому режиму, то есть (19)
 = 0, (19)
= 0, (19)
получаем линеаризованное уравнение в отклонениях от рабочей точки (20):
 , (20)
, (20)
где  и
и  коэффициент
коэффициент  зависит от
зависит от  , то есть от выбора рабочей точки. В этом проявляется нелинейность объекта. Обычно при записи линеаризованного уравнения знак Δ (обозначающий отклонение) не пишут. Таким образом, окончательно получаем линеаризованную модель (21)
, то есть от выбора рабочей точки. В этом проявляется нелинейность объекта. Обычно при записи линеаризованного уравнения знак Δ (обозначающий отклонение) не пишут. Таким образом, окончательно получаем линеаризованную модель (21)
 (21)
(21)
Но нужно помнить, что это уравнение в отклонениях, и оно справедливо только при малых отклонениях от рабочей точки ( ). При выборе другой рабочей точки коэффициент
). При выборе другой рабочей точки коэффициент  получится другой.
получится другой.
Посмотрим на этом примере, как можно управлять объектом и что из этого получается, немного изменив предыдущую задачу, разрешив потоку вытекающей жидкости  изменяться независимо (в ТАУ это называется нагрузкой на объект). Нужно построить систему, которая автоматически поддерживает заданный уровень
изменяться независимо (в ТАУ это называется нагрузкой на объект). Нужно построить систему, которая автоматически поддерживает заданный уровень  воды. Для управления уровнем воды
воды. Для управления уровнем воды  мы можем изменять его поток
мы можем изменять его поток  (м3/с). Таким образом, уровень
(м3/с). Таким образом, уровень  — это регулируемая величина, а поток
— это регулируемая величина, а поток  - сигнал управления. Для обратной связи используем датчик, измеряющий уровень воды
- сигнал управления. Для обратной связи используем датчик, измеряющий уровень воды  в баке.
в баке.
Если разность потоков постоянна в течение интервала времени  , то (22)
, то (22)
 . (22)
. (22)
В общем случае нужно использовать интеграл (23):
 (23)
(23)
Пусть в момент времени  = 0 уровень воды равен заданному значению, а входной и выходной потоки равны (
= 0 уровень воды равен заданному значению, а входной и выходной потоки равны ( ), так что уровень не меняется. Этот режим примем за номинальный - рабочую точку. Для того, чтобы получить уравнение в отклонениях, представим потоки в виде (24):
), так что уровень не меняется. Этот режим примем за номинальный - рабочую точку. Для того, чтобы получить уравнение в отклонениях, представим потоки в виде (24):
|
|
|
 (24)
(24)
где  и
и  - малые отклонения потоков от номинального режима.
- малые отклонения потоков от номинального режима.
Тогда, опуская знак приращения Δ, можно записать модель объекта управления в форме (25):
 (25)
(25)
где  ,
,  и
и  обозначают отклонения этих величин от номинальных значений. Эта модель может быть записана как дифференциальное уравнение (если найти производные обеих частей равенства) (26):
обозначают отклонения этих величин от номинальных значений. Эта модель может быть записана как дифференциальное уравнение (если найти производные обеих частей равенства) (26):
 . (26)
. (26)
СЛАЙД 12. Для упрощения далее примем  =1м2. В качестве обратной связи мы будем использовать сигнал с датчика уровня. Ошибка управления вычисляется как разница между заданным и измеренным уровнями воды (27):
=1м2. В качестве обратной связи мы будем использовать сигнал с датчика уровня. Ошибка управления вычисляется как разница между заданным и измеренным уровнями воды (27):
 . (27)
. (27)
Самый простой регулятор - усилитель с коэффициентом 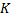 (или пропорциональный регулятор, П-регулятор), который управляет потоком по закону (28)
(или пропорциональный регулятор, П-регулятор), который управляет потоком по закону (28)
 (28)
(28)
Если проверить работу этого регулятора при различных значениях коэффициента 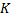 и считать, что шума измерений нет, то есть уровень измеряется точно. Расход воды на выходе
и считать, что шума измерений нет, то есть уровень измеряется точно. Расход воды на выходе  увеличивается скачком. Синяя линия на рисунке показывает изменение уровня при K = 1, а зеленая - при K = 5. По этим данным можно сделать следующие выводы:
увеличивается скачком. Синяя линия на рисунке показывает изменение уровня при K = 1, а зеленая - при K = 5. По этим данным можно сделать следующие выводы:
• при изменении нагрузки (потребления воды, потока  ) регулятор-усилитель не может поддерживать заданный уровень (графики не приходят к значению
) регулятор-усилитель не может поддерживать заданный уровень (графики не приходят к значению  = 0);
= 0);
• чем больше 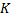 , тем меньше ошибка регулирования
, тем меньше ошибка регулирования  в установившемся режиме; можно ожидать, что при
в установившемся режиме; можно ожидать, что при  ошибка должна уменьшиться до нуля;
ошибка должна уменьшиться до нуля; 
• чем больше 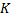 , тем быстрее заканчивается переход на новый режим.
, тем быстрее заканчивается переход на новый режим.
Кажется, что для улучшения управления нужно увеличивать 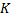 , однако это только первое впечатление.
, однако это только первое впечатление.
Если есть шум измерений (случайная ошибка датчика). По графикам видно, что при неточных измерениях уровень колеблется около некоторого среднего значения (того, что было получено без шума), причем при большем 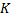 колебания увеличиваются. Этот эффект особенно хорошо виден на графике изменения расхода насоса
колебания увеличиваются. Этот эффект особенно хорошо виден на графике изменения расхода насоса  q (рисунок справа).
q (рисунок справа).
|
|
|
При увеличении 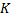 повышение точности (уменьшение установившейся ошибки) достигается за счет повышенной активности насоса, который все время «дергается». При этом механические части изнашиваются, и существенно уменьшается его срок службы. Поэтому коэффициент
повышение точности (уменьшение установившейся ошибки) достигается за счет повышенной активности насоса, который все время «дергается». При этом механические части изнашиваются, и существенно уменьшается его срок службы. Поэтому коэффициент 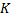 нельзя сильно увеличивать.
нельзя сильно увеличивать. 
Один из главных выводов этого примера: управление чаще всего связано с компромиссом. Здесь, с одной стороны, нужно увеличивать 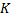 , чтобы повысить точность, а с другой - нужно уменьшать
, чтобы повысить точность, а с другой - нужно уменьшать 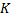 , чтобы уменьшить влияние шума измерения.
, чтобы уменьшить влияние шума измерения.
 2020-08-05
2020-08-05 100
100








