2020-08-05
128
СЛАЙД 30. Требования к управлению зависят от решаемой задачи. При стабилизации наиболее важны свойства установившегося режима. Для следящих систем нужно обеспечить высокое качество переходных процессов при изменении задающего сигнала (уставки). В целом можно выделить четыре основных требования:
• точность - в установившемся режиме система должна поддерживать заданное значение выхода системы, причем ошибка (разница между заданным и фактическим значением) не должна превышать допустимую;
• устойчивость - система должна оставаться устойчивой на всех режимах, не должна идти «вразнос»;
• качество переходных процессов - при смене заданного значения система должна переходить в нужное состояние по возможности быстро и плавно;
• робастность - система должна сохранять устойчивость и приемлемое качество даже в том случае, если динамика объекта и свойства внешних возмущений немного отличаются от тех, что использовались при проектировании.
Устойчивость.
СЛАЙД 31. Под термином «устойчивость» имеется в виду то, что устойчивая система возвращается в состояние равновесия, если какая-то сила выведет ее из этого состояния. Шарик на рисунке находится в устойчивом равновесии в положении А - если немного сдвинуть его с места, он скатится обратно в ямку.
Если шарик сильно отклонить от равновесия, он может свалиться через горку вбок, то есть устойчивость нарушится. В положениях Б и В шарик также находится в положении равновесия, но оно неустойчиво, так как при малейшем сдвиге в сторону шарик скатывается с вершины. В положениях Г и Д равновесие шарика нейтральное - при небольшом смещении он остается в новом положении. При этом говорят, что система нейтрально устойчива, то есть находится на границе устойчивости. Система «шарик-горка» - нелинейная, т. к. для нее: 
• устойчивость - не свойство системы, а свойство некоторого положения равновесия;
• может быть несколько положений равновесия, из них некоторые - устойчивые, а некоторые - нет;
• положение равновесия может быть устойчиво при малых отклонениях и неустойчиво при больших.
Устойчивость определяется для некоторого положения равновесия. Для нелинейной системы может быть несколько положений равновесия, причем некоторые из них могут быть устойчивы, а некоторые нет. В положении равновесия все производные равны нулю, то есть 
=0, где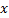 
- соответствующий вектор состояния. Предположим, что систему вывели в некоторое начальное состояние 
(задали начальные условия), а потом внешнее воздействие прекратили. Дальнейшее изменение координат («движение» системы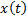 
) можно найти как решение уравнения при заданных начальных условиях.
Нестрого говоря, устойчивость означает, что все движения 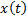, которые начинаются близко от положения равновесия 
, при всех 
остаются в некоторой окрестности . Лучше, конечно, если система не просто устойчива, а еще и возвращается в положение равновесия, то есть, 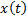стремится к при 
. В этом случае говорят об асимптотической устойчивости.
Рассмотрим маятник на рисунке а) справа, состоящий из подвешенного металлического стержня и шарика. Здесь положение равновесия - шарик в нижней точке. Если не учитывать трение, маятник, выведенный из положения равновесия, будет качаться бесконечно долго, причем амплитуда колебаний не будет увеличиваться, то есть, система устойчива. 
В реальности трение, конечно, есть, поэтому колебания маятника будут постепенно затухать (амплитуда уменьшается), и система, в конце концов вернется в положение равновесия. Это значит, что маятник с трением - асимптотически устойчивая система.
Маятник на рисунке б) тоже находится в положении равновесия, но оно неустойчиво: при малейшем отклонении маятник упадет вниз.
Формальное определение внутренней устойчивости было введено в работах А.М. Ляпунова, поэтому понятие устойчивости принято называть устойчивостью по Ляпунову, которым дано следующее определение:
Система называется устойчивой по Ляпунову в положении равновесия , если при начальном отклонении от положения равновесия не более, чем на 
, траектория движения отклоняется от не более, чем на 
, причем для каждого можно найти соответствующее ему 
:
при всех 
.
Обычно в ТАУ интересуются устойчивостью вынужденной составляющей 
переходного процесса. Поэтому за невозмущенное движение системы необходимо принять вынужденную составляющую переходного процесса . Тогда возмущенным движением будет любое возможное в системе изменение регулируемой величины 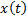, а отклонением или вариацией будет свободная составляющая 
.
СЛАЙД 32. Возмущениями по Ляпунову, являются начальные значения 
, которые возникли в момент 
под действием внезапно подействовавших дополнительных внешних сил, т.е. начальные значения 
. В соответствии с определением устойчивости по А.М.Ляпунову, система будет асимптотически устойчивой, если с течением времени при свободная составляющая будет стремится к нулю, т.е. 
. Чтобы найти эту составляющую, необходимо решить дифференциальное уравнение (1).
. (1)
Решение уравнения находят как (2)
. (2)
. Дифференцируя это выражение n раз получаем характеристическое уравнение (3):
. (3)
Его корни 
определяют характер переходного процесса в системе (его свободного движения).
Решение характеристического уравнение степени n содержит n корней. Корни характеристического уравнения обыкновенного линейного дифференциального уравнения с постоянными коэффициентами могут быть вещественными, комплексными попарно-сопряженными, мнимыми попарно-сопряженными, нулевыми. В общем случае (4)
. (4)
Комплексные корни характеристического уравнения всегда бывают попарно сопряженными (5)
и 
. (5)
Слагаемые, определяемые этими корнями определяем по формуле Эйлера (6)
, (6)
представлены в виде (7)
, (7)
где 
, 
– новые постоянные.
СЛУЧАЙ 33. В этом случае при 
получаются затухающие колебания (г) при 
-расходящиеся колебания (д) и при 
-незатухающие колебания (е). Для устойчивости в этом случае необходимо выполнение условий 
при 
.
Таким образом, процесс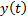 
затухает при любых начальных условиях тогда и только тогда, когда все корни 
(
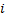=1...n) имеют отрицательные вещественные части. В этом случае система асимптотически устойчива.
СЛАЙД 34. Фактически это означает, что чем меньше начальное отклонение, тем меньше траектория движения отклоняется от положения равновесия. Если, кроме того, вектор состояния стремится к положению равновесия, то есть, (8)
при всех , (8)
система называется асимптотически устойчивой в положении равновесия .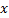
Очевидно, что асимптотическая устойчивость более сильное требование. Положения равновесия, которые устойчивы по Ляпунову, но не асимптотически устойчивы, иногда называются нейтрально устойчивыми (маятник без трения, ванна с водой).
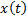Положение равновесия неустойчиво, если для него не выполняется условие устойчивости Ляпунова. Это значит, что существует такое >0, что траектория выходит за границы области (9)
(9)
при сколь угодно малом отклонении начального состояния 
от положения равновесия . Например, система переходит в другое положение равновесия, или 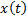неограниченно возрастает. На следующем рисунке показаны движения устойчивой, асимптотически устойчивой и неустойчивой систем первого порядка (с одной координатой ).
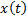Линейные системы обладают рядом особенностей, которые во многих случаях упрощают анализ устойчивости:
• автономная линейная система (на которую не действуют внешние силы) может иметь единственное положение равновесия (в котором все сигналы равны нулю) или бесконечно много положений равновесия (шарик на плоской поверхности);
• устойчивость - это свойство линейной системы, а не отдельного положения равновесия: или все ее движения устойчивы (асимптотически устойчивы), или все неустойчивы;
• асимптотическая устойчивость линейной системы «в малом» сразу означает ее устойчивость «в целом», то есть, при любых отклонениях от положения равновесия;
• асимптотически устойчивая система также обладает устойчивостью «вход-выход», а просто устойчивая (нейтрально устойчивая, не асимптотически устойчивая) - нет.
