2020-08-05
287
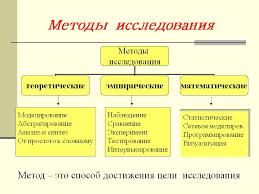
Пусть задано некоторое (конечное или бесконечное) множество G, на котором определена операция умножения, т. е. определен закон, сопоставляющий любой паре a, b элементов из G некий элемент из G называемый произведением а и b и обозначаемый Символом а ∙ b. Предположим, что эта операция умножения удовлетворяет следующим условиям:
I. Условие ассоциативности. Для любых трех элементов a, b, c множества G справедливо соотношение:
Это значит следующее. Обозначим через d элемент множества G, являющийся произведением элементов a и b\ точно так же обозначим через е элемент b ∙ c множества G. Тогда d∙c и a∙e являются одним и тем же элементом множества G.
II. Условие существования нейтрального элемента. Среди элементов множества G имеется некоторый определенный элемент, называемый нейтральным элементом и обозначаемый символом 1, такой, что
III. Условие существования обратного элемента к каждому данному элементу. К каждому данному элементу a множества G можно подобрать такой элемент b того же множества G, что
Элемент b называется обратным к элементу a и обозначается а -1.
Множество G с определенной в нем операцией умножения, удовлетворяющей только что перечисленным трем условиям, называется группой; сами эти условия называются аксиомами группы.
Операция умножения, удовлетворяющая аксиомам группы, иногда называется групповой операцией
Пусть в группе G, кроме указанных выше трех аксиом, оказывается выполненным еще и следующее условие:
IV. Условие коммутативности:
В этом случае группа G называется коммутативной или абелевой группой.
Группа называется конечной, если она состоит из конечного числа элементов; в противном случае она называется бесконечной.
Число элементов конечной группы называется ее порядком.
1) с группой целых чисел (групповая операция - обычное сложение целых чисел);
2) с группой отличных от нуля рациональных чисел (групповая операция - обычное умножение рациональных чисел);
3) с группой поворотов правильного треугольника (групповая операция-композиция поворотов);
4) с клейновской группой порядка 4 (групповая операция-умножение букв a0, a1, a2, a3, задаваемое таблицей 2);
5) с группой поворотов правильного четырехугольника (групповая операция- композиция поворотов);
6) с группой поворотов правильного «-угольника.
Все эти группы коммутативны. Группа целых чисел и группа ненулевых рациональных чисел бесконечны; остальные - конечные группы.
Порядок элемента обозначается 
. Заметим, что 
тогда и только тогда, когда 
.
Следующее предложение объясняет, почему для порядка группы и порядка элемента используется одно и то же слово.
Предложение Пусть G - группа и 
. Тогда 
.
Доказательство. Заметим, что если 
, то 
. Поэтому если элемент g имеет бесконечный порядок, то все элементы 
, попарно различны, и подгруппа 
содержит бесконечно много элементов. Если же порядок элемента д равен т. то из минимальности числа т следует, что элементы 
попарно различны. Далее, для всякого 
мы имеем 
, где 
, и
Следовательно, 
и 
Определение Группа G называется циклической, если найдётся такой элемент , что 
.
Ясно, что любая циклическая группа коммутативна и не более чем счётна. Примерами циклических групп являются группы (Z, +) и (Zn,+), n≥1.
Перейдем ещё к одному сюжету, связанному с парой группа-подгруппа.
Определение 11. Пусть G - группа, 
- подгруппа и . Левым смежным классом элемента g группы G по подгруппе Н называется подмножество
Лемма 1. Пусть G - группа, - её подгруппа и 
. Тогда либо 
, либо 
.
Доказательство. Предположим, что 
, т. е. 
Для некоторых 
. Нужно доказать, что . Заметим, что 
. Обратное включение доказывается аналогично.
Лемма 2. Пусть G - группа и конечная подгруппа. Тогда 
для любого .
Доказательство. Поскольку 
. в 
элементов не больше, чем в Н. Если 
, то домножаем слева на g-1 и получаем h1 = h2. Значит, все элементы вида gh. где 
, попарно различны, откуда 
Определение Пусть G - группа и подгруппа. Индексам подгруппы H в группе G называется число левых смежных классов G по H.
Индекс группы G по подгруппе Я обозначается [G: H].
Теорема Лагранжа. Пусть G конечная группа и подгруппа. Тогда
Доказательство. Каждый элемент группы G лежит в (своём) левом смежном классе по подгруппе H. разные смежные классы не пересекаются (лемма 1) и каждый из них содержит по 
элементов (лемма 2).
Следствие 1. Пусть G - конечная группа и - подгруппа. Тогда 
делит 
.
Следствие 2. Пусть G - конечная группа и . Тогда ord(g) делит .
Доказательство. Это вытекает из следствия 1 и предложения 2.
Следствие 3. Пусть G - конечная группа и . Тогда 
.
Доказательство. Согласно следствию 2, мы имеем 
. откуда 
.
Следствие 4 (Малая теорема Ферма). Пусть 
- ненулевой вычет по простому модулю р. Тогда
Доказательство. Вытекает из следствия 3, применённого к группе (Zp\{0},х).
Следствие 5. Пусть G - группа. Предположим, что |G| - простое число. Тогда G - циклическая группа, порождаемая любым своим неединичным элементом.
Доказательство. Пусть - произвольный неединичный элемент. Тогда циклическая подгруппа содержит более одного элемента и 
делит |G| но следствию 1. Значит, 
, откуда
Наряду с левым смежным классом можно определить правый смежный класс элемента д группы G но подгруппе H:
Повторяя доказательство теоремы Лагранжа для правых смежных классов, мы получим, что для конечной группы G число правых смежных классов по подгруппе Н равно числу левых смежных классов и равно 
. В то же время равенство 
выполнено не всегда. Разумеется, оно выполнено, если группа G абелева. Подгруппы H (неабелевых) групп G\ для которых выполнено для любого . будут изучаться в следующей лекции.
