Пусть  точка регулярной поверхности
точка регулярной поверхности 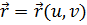 . В этой точке имеем неколлинеарные векторы
. В этой точке имеем неколлинеарные векторы 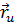 ,
, 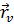 . Для любой линии
. Для любой линии  выполняется
выполняется
 ,
,
т.е. вектор касательной  всякой линии поверхности
всякой линии поверхности  , проходящей через точку
, проходящей через точку  , является линейной комбинацией векторов
, является линейной комбинацией векторов 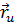 ,
, 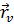 - векторов касательных -линии и
- векторов касательных -линии и 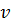 -линии; вектор
-линии; вектор  принадлежит оболочке
принадлежит оболочке  . Касательная прямая
. Касательная прямая  всякой кривой
всякой кривой  поверхности
поверхности 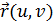 лежит в плоскости
лежит в плоскости  . Касательные всех линий поверхности
. Касательные всех линий поверхности 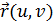 , проходящих через точку
, проходящих через точку  , образуют плоскость. Получена следующая
, образуют плоскость. Получена следующая
III.3.1. ТЕОРЕМА. Регулярная поверхность 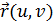 в каждой своей точке
в каждой своей точке  обладает касательной плоскостью <
обладает касательной плоскостью <  . #
. #
Пусть  и производные
и производные 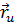 ,
, 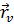 вычислены в точке
вычислены в точке  . Тогда уравнение касательной плоскости таково
. Тогда уравнение касательной плоскости таково
 .
.
Прямая  называется нормалью поверхности
называется нормалью поверхности  в точке
в точке  . Ее уравнения:
. Ее уравнения:
 .
.
III.4. ПЕРВАЯ ОСНОВНАЯ КВАДРАТИЧНАЯ ФОРМА ПОВЕРХНОСТИ.
В произвольной точке  поверхности
поверхности 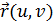 зададим направление, выбрав
зададим направление, выбрав 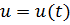 ,
, 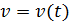 . Отношение дифференциалов
. Отношение дифференциалов

определяет направление на поверхности, имеем
 .
.
Производная от 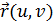 по направлению
по направлению  имеет вид
имеет вид
 .
.
Малое смещение  по кривой
по кривой  на поверхности вычисляется на основании равенств
на поверхности вычисляется на основании равенств
 .
.
Отсюда получаем, вычисляя скалярный квадрат  ,
,
 . (III.4.1)
. (III.4.1)
Введем обозначения:
 ,
,  ,
,  . (III.4.2)
. (III.4.2)
Значения этих скалярных произведений зависят от выбора точки  поверхности. Выражение
поверхности. Выражение
 . (III.4.3)
. (III.4.3)
называется первой основной квадратичной формой поверхности 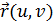 .
.
 2020-08-05
2020-08-05 91
91








