Общие замечания
Сопряжением называют плавный переход от линии a к линии b посредством сопрягающей линии c (рис. 20).

Рис. 20
Точки А и В в которых одна линия плавно переходит в другую называют точками стыка или точками сопряжения. Сопряжение считается выполненным, если в точках стыка к сопрягающимся кривым можно провести общие касательные ta и tb. Через каждую точку стыка проходит нормаль n, перпендикулярная касательной.
В большинстве случаев приходится строить сопряжения, когда линии a и b являются прямыми или окружностями.
Для построения сопряжения должны быть известны три элемента:
1) радиус R сопрягающей дуги c;
2) одна из точек стыка (любая) А или В;
3) точка О – центр сопрягающей дуги с.
Заданием одного из этих элементов (любого) определяются остальные. На практике чаще всего задают либо радиус сопряжения, либо одну из точек стыка.
При решении задач на сопряжения полезно рассматривать прямые как окружности с бесконечно-большим радиусом, а точки – как окружности с бесконечно-малым радиусом.
2.2. Основные задачи
Задача 1. Построить сопряжение окружности a и прямой b посредством дуги с радиуса R (рис. 21).
1. Строим прямую b', параллельную b и отстоящую от неё на расстояние R.
2. Строим окружность a' концентрическую окружности a и отстоящую
от a на такое же расстояние R, т.е. радиус окружности a' будет равен
r + R;
3. На пересечении линий b' и a' находим т. О1, равноудалённую от
окружности a и прямой b, которая и есть искомый центр сопряжения.
4. Точку стыка А находим на пересечении окружности a c прямой ОО1,
а точка В лежит в основании перпендикуляра, опущенного из центра О1
на прямую b.
5. Строим сопрягающую дугу с из центра О1.
6. Касательные, проведённые в точках стыка А и В, располагаются
соответственно ta ^ ОО1, а tb ≡ b.


Рис. 21 Рис. 22
Для случая, когда линии a и b – окружности, а величина радиуса R едва превышает расстояние между окружностями (рис. 22), строим окружность а' радиуса r1 + R, концентрическую окружности а и окружность b' радиуса r2 + R, концентрическую окружности b. Окружности a ' и b' отстоят от соответствующих a и b на одинаковом расстоянии R. Такие линии называют эквидистантами (от лат. aequidistans — равноудалённый). Искомый центр О сопряжения лежит на пересечении a ' и b'. Дальнейшее – ясно из чертежа.
Задача 2. Построить сопряжение окружностей a и b посредством дуги с заданного радиуса R (рис. 23).

Рис. 23
1. Строим эквидистанты окружностей a и b с радиусами соответственно
R–r1 и R–r2.
2. В пересечении эквидистант находим центр О.
3. Проводим через О и центры О1 и О2 прямые и с их помощью находим
точки стыка А и В.
В отличие от рассмотренной задачи, когда известен радиус сопрягающей дуги, встречаются задачи, когда известной оказывается одна из точек стыка – А или В. В этом случае для построения сопряжения удобно использовать радикальную ось k, свойство которой состоит в том, что касательные, проведённые из любой её точки к двум неконцентрическим окружностям – равны. Иначе говоря, радикальная ось – это геометрическое место точек пересечения равных между собой касательных к двум окружностям.
На рис. 24 точки M и N радикальной оси k равноудалены соответственно от точек касания А, В, Н и Т, а также от точек С и D.
Если центры О1, О2 и О3 трёх окружностей линейно независимы, то радикальные оси этих трёх окружностей, взятые попарно, проходят через одну точку М, называемую радикальным центром.
Если радикальный центр лежит вне каждой из трёх окружностей (рис. 24), то из него к данным окружностям можно провести равные касательные:
МА = МН = МТ = МВ (подробнее о радикальной оси см. (5)).

Рис. 24
Задача 2. Построить сопряжение окружности a и прямой b, если на окружности задана точка стыка А (рис. 25).
Один из искомых центров сопряжения должен лежать на прямой ОА1.
1. Проведем касательную tа к окружности в т. А.
2. Построим радикальный центр М: М = tа ∩ b.
3. Из т. М проводим дугу радиуса МА1 и находим с её помощью точки стыка
А2 Ì a и В Ì b.
4. Строим прямую n É В → n ^ b. Нахождение центров сопряжения О1 и О2 на прямой n ясно из чертежа.

Рис. 25
Задача 3. Построить сопряжение окружности a и прямой b, на которой задана точка стыка В (рис. 26).
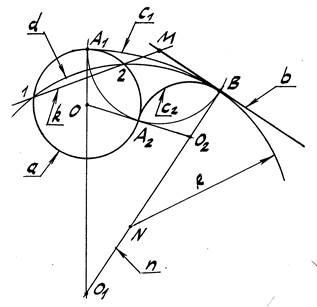
Рис. 26
1. Из т. В восставляем перпендикуляр n к прямой b.
2. Из произвольной т. N перпендикуляра n проводим окружность d радиуса R=NB.
3. Через точки 1 и 2 пересечения окружностей a и d проводим радикальную ось k.
4. Находим радикальный центр М: М= k ∩ b.
5. Из центра М проводим дугу радиуса МВ в пересечении которой с окружностью а найдем искомые точки стыка А1 и А2; прямые А1О и А2О пересекаются с прямой n соответственно в центрах сопряжения О1 и О2. Искомые дуги сопряжения – с1 и с2.
Задача 4. Построить сопряжение окружностей a и b, если задана точка стыка А Ì a (рис. 27).
1. Проведём касательную ta к окружности а в точке стыка А и, тем самым,
сведём данную задачу к задаче 2, т.е. будем строить сопряжение
окружности b и прямой ta.

Рис. 27
Окружности с бесконечно-малым радиусом вырождаются в точки, и в этом случае задача на построение сопряжения переходит в задачу построения обводов точек.
2.3. Построение обводов
Обводом или интерполированием точек А1, А2, А3,…, заданных на плоскости называется кривая последовательно составленная из дуг А1А2, А2А3, …и т.д. (рис. 28).

Рис. 28
Если указанные дуги имеют в точках стыка общие касательные, то обвод называется гладким и представляет собой коробовую линию (см. далее).
Коробовую линию можно составить из дуг окружностей. Такие линии находят широкое применение в технике, строительстве и архитектуре. Для построения циркульных коробовых кривых применяют радиус-графический способ.
Задача. Даны пять произвольных тт. А1, А2, А3, А4, А5. Требуется выполнить их обвод дугами окружностей (рис. 29).

Рис. 29
Начальными параметрами, которые зададут форму всему обводу, будут либо направление касательной t1 в точке А1, либо радиус дуги А1А2 – радиус кривизны r1.
1. Соединим заданные точки отрезками прямых в указанной
последовательности, а затем через середину каждого отрезка
восстановим к ним перпендикуляры – на них будут располагаться
центры дуг обвода – О1, О2, О3, и О4.
2. Зададим касательную t1 É А1.
3. Построим центр О1 первой дуги с помощью нормали n: nÉ А1 → n ^ t1.
4. Центр О2 следующей дуги А2А3 лежит на пересечении прямых n' и b.
Дальнейшие построения ведутся аналогичным образом и в той же последовательности. Форму обвода можно видоизменять, если изменять начальные параметры.
На рис. 30 дан пример построения поверхности вращения, которая в архитектурной практике носит название "маковки". Главный меридиан "маковки" складывается из четырёх составляющих (из них три дуги окружности, образующие обвод первого порядка гладкости).

Рис. 30
Построение овалов
3.1. Основные задачи
Замкнутая кривая, образованная сопряжением циркульных кривых, называется овалом.
· Овалы с одной осью симметрии называются овоидами.
· Овалы с двумя осями симметрии называются коробовыми кривыми. Коробовые кривые часто используют в качестве замены эллипсу при построении аксонометрических изображений окружности.
Задача 1. Построить нормальный овоид заданного радиуса R (рис. 31).
1. Проводим из центра О окружность k радиуса R.
2. Тт. О1 и О2 соединяем с т. О3 пересечения вертикальной оси и
окружности k.
3. Проводим из центров О1 и О2 дуги, радиуса R2 = 2R до их
пересечения с прямыми m и n в точках 1 и 2.
3. Из центра О3 проводим дугу радиуса R3, замыкая овоид.
Построение остроконечного (рис. 32) и тупоконечного (рис. 33) овоида
заданного радиуса R аналогично построениям на рис. 31.



Рис. 31 Рис. 32 Рис. 33
Если привести форму данных овоидов в симметричную относительно ещё
и горизонтальной оси, они станут овалами. Ниже приводятся некоторые способы построения овала.
Задача 2. Построить овал (коробовую кривую) по заданной его оси АВ
(рис. 34).
1. Разделим АВ на 4 равные части: АО1 = О1О = ОО2 = О2В.
2. Из полученных точек О1 и О2 радиусом R делаем засечки, получая
таким образом центры О3 и О4.
3. Из центра О1 радиусом R1 проводим дугу до её пересечения с прямыми m
и m' в точках 1 и 2. Аналогично находим тт. 3 и 4.
4. Дуги 1-3 и 2-4 проводим радиусом R2 из центров О3 и О4.
Если заданную ось АВ разделить точками О1 и О2 на три равные части,
построение овала будет аналогичным (рис. 35).

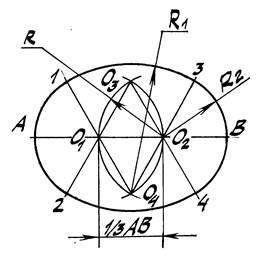
Рис. 34 Рис. 35
Задача 3. Построить овал по двум его взаимно-перпендикулярным осям
АВ и СD (рис. 36).

Рис. 36
1. На вертикальной оси i с помощью дуги радиуса ОА строим т. Е
(ОА=ОЕ).
2. Соединим тт. А и С, и от т. С отложим на этой прямой отрезок КС=ЕС.
3. Через середину отрезка АК проводим перпендикуляр m и находим в
его пересечении с осями АВ и СD овала тт. О1 и О4, а затем и
симметричные им тт. О2 и О3.
Тогда О1, О2, О3 и О4 есть центры сопряжений, а 1, 2, 3 и 4 – точки стыка.
Задача 4. Построить овал по двум его осям, если малая ось СD втрое меньше большой l(А,В) (рис. 37).
1. Строим центры О1 и О2, откладывая на оси АВ от тт. А и В вправо и
влево отрезки, равные 1/12 l (используем для этого теорему Фалеса).
2. Строим центры О3 и О4, откладывая от т. О вверх и вниз отрезки, равные l.
3. Строим пары сопрягающихся дуг радиусами R и R' и в результате находим
точки стыка 1, 2, 3 и 4 ясно из чертежа.
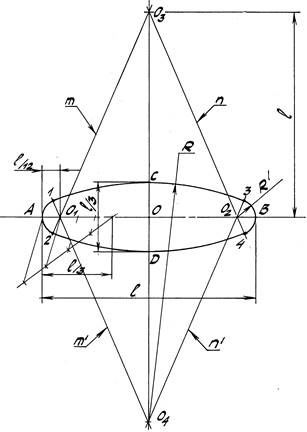
Рис. 37
Задача 5. Построить овал по двум его осям АВ и СD (рис. 38).
1. На полуоси АО строим равносторонний треугольник АМО.
2. Радиусом R= ОС делаем засечку С' на стороне ОМ.
3. Соединяем С и С' и продолжаем эту прямую до пересечения со стороной
АМ в т. 1.
4. Через т. 1 проводим прямую m' ║ ОМ.
5. Прямая m' пересекается с осями АВ и СD в точках О1 и О4.

Рис. 38
6. Находим тт. О2 и О3, симметричные О1 и О4 осей овала и получаем, таким образом, четыре центра сопряжений для дуг с точками стыка 1, 2, 3 и 4.
 2020-08-05
2020-08-05 529
529








