2020-09-24
1046
Вероятность принятия ошибочного решения слагается из вероятностей ложной тревоги и пропуска дефекта. Если приписать «цены» этим ошибкам, то получим выражение для среднего риска
 | (9.1) |
где диагноз D 1 соответствует исправному, а D 2 – дефектному состоянию объекта; C 21 – цена ложной тревоги; C 12 – цена пропуска дефекта (первый индекс – принятое состояние, второе – действительное); C 11, С 22 – цены правильных решений (условные выигрыши), которые для сравнения со стоимостью потерь (ошибок) принимается отрицательными. В задачах надёжности стоимость пропуска дефекта обычно существенно больше стоимости ложной тревоги (С 12>> С 21).
Разумеется, цена ошибки имеет условное значение, но она должна учесть предполагаемые последствия ложной тревоги и пропуска дефекта.
Иногда цены правильных решений C 11и С 22 принимают равными нулю. Тогда средний риск (ожидаемая величина потери) выражается равенством
 | (9.2) |
Величина x, предъявляемая для распознавания, является случайной и потому равенства (9.1) и (9.2) представляют собой среднее значение (математическое ожидание) риска.
Найдём граничное значение x 0из условия минимума функции среднего риска
 | (9.3) |
Дифференцируя (9.3) по x и приравнивая производную нулю, получим условие экстремума
 , | (9.4) |
или
 | (9.5) |
Это условие часто определяет два значения x 0, из которых одно соответствует минимуму, второе – максимуму риска (Рис. 8.1). Соотношение (9.5) является необходимым, но недостаточным условием минимума. Для существования минимума R в точке x=x 0вторая производная должна быть положительной 
, что приводит к следующему условию относительно производных плотностей распределений:
 | (9.6) |
Если распределения 
и 
являются, как обычно, одномодальными (т.е. содержат не более одной точки максимума), то при
 , | (9.7) |
условие (9.6) выполняется. Действительно, в правой части равенства стоит положительная величина, а при 
производная f’ (x / D 1)<0, тогда как при 
значение f ' (x / D 2)>0.
В дальнейшем под x 0будем понимать граничное значение диагностического параметра, обеспечивающее по правилу (9.2) минимум среднего риска. Будем также считать распределения f (x / D 2) и f (x / D 1) одномодальными («одногорбыми»).
Из условия (9.5) следует, что решение об отнесении объекта при заданном x к состоянию D 1 или D 2 можно связать с величиной отношения правдоподобия. Напомним, что отношение плотностей вероятностей распределения при двух состояниях называется отношением правдоподобия.
По методу минимального риска принимается следующее решение о состоянии объекта, имеющего данное значение параметра x:
 , если  ; | (9.8) |
 , если  . | (9.9) |
Эти условия вытекают из соотношений (9.1) и (9.5).
Условие (9.8) соответствует x<x 0, условие (9.9) x>x 0 Величина 
представляет собой пороговое значение для отношения правдоподобия. Учтём, что диагноз D 1 соответствует исправному состоянию, D 2 – неисправному (дефектному) состоянию объекта; C 21 – цена ложной тревоги; C 12 – цена пропуска дефекта (первый индекс – принятое состояние, второе – действительное); C 11 < 0, C 22 < 0 – цены правильных решений (условные выигрыши). В большинстве практических задач условные выигрыши (поощрения) для правильных решений не вводятся, и тогда получим
 . | (9.10) |
Часто оказывается удобным рассматривать не отношение правдоподобия, а логарифм этого отношения. Это не изменяет результата, так как логарифмическая функция возрастает монотонно вместе со своим аргументом. Расчёт для нормального и некоторых других распределений при использовании логарифма отношения правдоподобия оказывается несколько проще.
Рассмотрим случай, когда параметр x имеет нормальное распределение при исправном D 1 и неисправном D 2 состояниях. Рассеяние параметра (величина среднеквадратичного отклонения) принимается одинаковым.
В рассматриваемом случае плотности вероятности
 | (9.11) |
Подставляя эти соотношения в равенство (9.5) и обозначая х = х 0, после логарифмирования получаем
 | (9.12) |
Из этого уравнения (9.12) получим
 | (9.13) |
При 
величина 
; при 
случайная величина 
.
Для случая σ 1 ¹ σ 2, т.е.
 | (9.14) |
получим следующие выражения
 , | |
 . | (9.15) |
Решая это уравнение, получим квадратное уравнение следующего вида:
 , | (9.16) |
здесь 
.
Напомним, что 
.
Пример
Задача. Диагностика механизма осуществляется по температуре подшипниковых узлов. Установлено, что для исправного состояния среднее значение температуры подшипникового узла составляет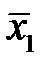 
=50°C и среднее квадратичное отклонение σ 1=15°C. При наличии повышенного износа 
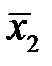=100°C, σ 2=25°C. Распределения предполагаются нормальными.
Определить предельное значение x 0, рассчитать вероятность ложной тревоги, вероятность пропуска дефекта и средний риск
, 
, 
, 
.
Так как сумма вероятностей исправного и неисправного состояний равна единице, то
.
На рис. 9.1 приведены графики следующих функций: Рис. 9.1
,
.
Рис. 9.1. Исходные плотности вероятности признаков
На рис. 9.2 приведены графики с учётом априорных вероятностей исправного и неисправного состояний: Рис. 9.2
,
.
Рис. 9.2. Плотности вероятности с учётом априорной вероятности
На рис. 9.3 приведены графики функций с учётом априорных вероятностей состояний и стоимостей принятия решений, а также функция риска R (x): Рис. 9.3
,
,
Рис. 9.3. Плотности вероятности с учётом априорных вероятностей,стоимости ложной тревоги и стоимости пропуска дефекта, функция риска R (x)
Решение. По методу минимального риска:
.
Выразим выражение (С 12 – С 22)/(С 21 – С 11) из имеющихся данных.
, 
,
.
Получим
,
где плотности распределения равны:
,
.
Подставив полученные плотности распределения в формулу выше, получим квадратное уравнение относительно х = х 0:
.
Подставим известные значения и решим уравнение.
.
Это уравнение имеет положительный корень x 0 = 65,698°C.
Проведём проверку:
, 
,
, 
.
Теперь найдём вероятность ложной тревоги и пропуска дефекта:
,
.
Далее найдём средний риск по формуле (9.1):
.
Выводы.
В результате расчёта по методу минимального риска получили предельное значение диагностического параметра x 0 = 65,698°C, выше которого исследуемый объект подлежит снятию с эксплуатации. При этом вероятность ложной тревоги составляет РЛТ = 0,1225, вероятность пропуска дефекта РПД = 0,0128. Найдена величина среднего риска, которая составляет
R = – 0,119 C 21.
Контрольные вопросы
1. Дайте определение отношению правдоподобия.
2. Поясните понятие «вероятность ложной тревоги».
3. Поясните понятие «вероятность пропуска цели (дефекта)».
4. Каков критерий метода минимально риска?
