2020-10-12
157
Пусть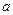 
– число или один из символов 
; 
; 
.
Теорема 1. Предел постоянного равен этому постоянному: 
.
Если 
и 
при 
имеют конечные пределы, то справедливы следующие теоремы:
Теорема 2. 
.
Теорема 3. 
.
Теорема 4. 
при условии 
.
Рассмотрим некоторые замечательные пределы.
Пусть 
,
(
, 
).
Тогда 
Пример 4. 
Пример 5. 
называют первым замечательным пределом.
Пример 6. 
называют вторым замечательным пределом.
Если в этом равенстве положить 
(
, то 
), то оно запишется в виде 
.
Пример 7. 
Пример 8. Найти 
Преобразуем выражение в скобках, выполнив деление «уголком» числителя на знаменатель. Получаем 
. Пусть 
, тогда 
и 
, причем при имеем . Следовательно, 
.
Некоторые приемы вычисления пределов функций
Для того, чтобы найти предел элементарной функции, когда аргумент стремится к значению, принадлежащему области определения этой функции, нужно в выражении функции вместо аргумента подставить его предельное значение.
.
Под знаком предела можно производить тождественные преобразования аналитического выражения, задающего функцию, не принимая во внимание поведение функции в предельной точке. В частности, например, под знаком предела можно производить сокращение дроби на множитель, обращающийся в предельной точке в нуль (но не равный нулю в близи этой точки!).
Пример 9. 
Пример 10. 
Разложим числитель и знаменатель на множители, используя формулы
,
, где 
, 
, 
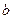– числа, 
, 
, 
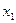– корни квадратного трехчлена. Получаем:
.
Пример 11. Найти 
Числитель и знаменатель дроби умножим на выражение, сопряженное числителю, получаем:
.
Пример 12. Найти 
В данном примере при выяснении вида неопределенности видим, что таковой не имеется.
Имеем 
, тогда 
.
