Определение: Функция 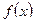 , определенная в точке
, определенная в точке  и некоторой окрестности, называется непрерывной в точке
и некоторой окрестности, называется непрерывной в точке  , если предел функции при
, если предел функции при  равен значению функции в точке
равен значению функции в точке  :
:  .
.
Любая элементарная функция непрерывна в ее области определения.
Определение: Если функция  определена в окрестности точки
определена в окрестности точки  (кроме, быть может, самой точки
(кроме, быть может, самой точки  ) и не является непрерывной в этой точке, то ее называют разрывной в точке
) и не является непрерывной в этой точке, то ее называют разрывной в точке  . В этом случае точку
. В этом случае точку  называют точкой разрыва
называют точкой разрыва 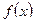 .
.
Определение: Функция  называется непрерывной на интервале
называется непрерывной на интервале  , если она непрерывна в каждой точке интервала. Функция
, если она непрерывна в каждой точке интервала. Функция  называется непрерывной на отрезке
называется непрерывной на отрезке  , если она непрерывна на интервале
, если она непрерывна на интервале  и, кроме того, непрерывна справа в точке
и, кроме того, непрерывна справа в точке 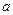 и непрерывна слева в точке
и непрерывна слева в точке 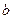 .
.
Для непрерывности функции на отрезке  не требуется непрерывность этой функции на концах отрезка. В точках
не требуется непрерывность этой функции на концах отрезка. В точках 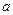 и
и  требуется только односторонняя непрерывность функции для левого конца непрерывность справа, для правого непрерывность слева.
требуется только односторонняя непрерывность функции для левого конца непрерывность справа, для правого непрерывность слева.
Из определения точки разрыва функции получаем, что точка  является точкой разрыва функции
является точкой разрыва функции  , если выполняется одно из условий: или функция
, если выполняется одно из условий: или функция  определена в точке
определена в точке  , но не является непрерывной в этой точке, или функция
, но не является непрерывной в этой точке, или функция  не определена в точке
не определена в точке  .
.
В первом случае  принадлежит области определения функции, во втором случае
принадлежит области определения функции, во втором случае  не принадлежит области определения функции. Для основных элементарных функций возможен только второй случай.
не принадлежит области определения функции. Для основных элементарных функций возможен только второй случай.
Пусть  – точка разрыва функции
– точка разрыва функции  . При этом
. При этом  называется точкой разрыва первого рода, если функция
называется точкой разрыва первого рода, если функция  имеет конечные пределы справа и слева в этой точке. Во всех остальных случаях
имеет конечные пределы справа и слева в этой точке. Во всех остальных случаях  называется точкой разрыва второго рода. Если
называется точкой разрыва второго рода. Если  – точка разрыва I рода функции
– точка разрыва I рода функции  , то график этой функции в точке
, то график этой функции в точке  может иметь лишь конечный скачок. Если же
может иметь лишь конечный скачок. Если же  – точка разрыва I рода функции
– точка разрыва I рода функции  , то, по крайней мере, один из пределов справа или слева в точке
, то, по крайней мере, один из пределов справа или слева в точке  не существует или равен бесконечности.
не существует или равен бесконечности.
Пример 13. Исследовать функцию на непрерывность и построить её график


Эта функция определена на интервалах  ,
,  ,
,  , где она задана непрерывными элементарными функциями. Внутри каждого интервала указанные элементарные функции не имеют точек разрыва, следовательно, разрыв возможен только в точках перехода от одного аналитического выражения к другому, т.е. в точках
, где она задана непрерывными элементарными функциями. Внутри каждого интервала указанные элементарные функции не имеют точек разрыва, следовательно, разрыв возможен только в точках перехода от одного аналитического выражения к другому, т.е. в точках 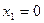 и
и  .
.
Для точки 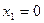 имеем:
имеем:
 ,
,  ,
,

Так как  , то функция
, то функция  в точке
в точке 
 имеет разрыв первого рода. Для точки
имеет разрыв первого рода. Для точки  находим
находим
 ,
,
 .
.
Значение функции в самой точке  равно
равно  .
.
 .
.
Так как  , то функция
, то функция  в точке
в точке 
 имеет разрыв первого рода. Изобразим график функции
имеет разрыв первого рода. Изобразим график функции 

Пример 14. Исследовать данную функцию на непрерывность в указанных точках  ;
;  ,
,  .
.
Для точки  имеем:
имеем:
 ,
,
 ,
,
т.е. в точке  функция
функция  имеет разрыв второго рода (терпит бесконечный разрыв). Для точки
имеет разрыв второго рода (терпит бесконечный разрыв). Для точки  имеем:
имеем:
 ,
,
 ,
,
 .
.
Следовательно, в точке  функция
функция  непрерывна.
непрерывна.
 2020-10-12
2020-10-12 141
141








