2020-10-12
130
Рассмотрим линии, уравнение которых в декартовой системе координат являются алгебраическими уравнениями второй степени, т.е. будем рассматривать алгебраические кривые второго порядка.
Общее уравнение кривых второго порядка:
Нормальное уравнение окружности радиуса 
с центром в точках 
и 
соответственно имеет вид:
Каноническое уравнение эллипса (координатные оси совпадают с осями эллипса):
где 
и 
– оси эллипса:
и 
– фокусы эллипса, если 
Каноническое уравнение гиперболы (оси координат совпадают с осями гиперболы):
,
где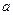 
и – соответственно действительная и мнимая полуоси гиперболы;
и 
– фокусы эллипса, если 
.
Каноническое уравнение параболы с вершиной в начале координат имеет вид:
(если она симметрична относительно оси 
), или 
, 
(если она симметрична относительно оси 
Задача 3.
Определить расположение и вид следующих кривых второго порядка:
1) 
2) 
3) 
4) 
5) 
6) 
Решение:
1) 
Выделим полные квадраты
Это уравнение эллипса, центр которого лежит в точке 
, а полуоси равны 
|
|
|
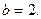
2) 
Это уравнение кривой, выродившейся в точку 
3) 
Уравнение является уравнением гиперболы с центром в точке 
и полуосями, равными 
; 
.
4) 
Это уравнение является уравнением пары прямых 
, 
, пересекающих в точке 
5) 
Это уравнение является уравнением параболы с осью симметрии, параллельными влево, с вершиной 
и фокальным параметром 
6) 
Полученное уравнение является уравнением параболы с осью симметрии, направленными вверх, с вершиной 
и фокальным параметром 
