1. Испытания и события. Их классификация.
2. Классическое, статистическое и геометрическое определения вероятности случайного события.
3. Основные понятия и формулы комбинаторики.
4. Теорема сложения вероятностей несовместных событий.
5. Полная группа событий, противоположные события.
6. Произведение событий.
7. Условная вероятность.
8. Теорема умножения вероятностей.
9. Независимые события. Теорема умножения для независимых событий.
10. Теорема сложения вероятностей совместных событий.
11. Формула полной вероятности.
12. Вероятность гипотез. Формула Бейеса.
13. Формула Бернулли.
14. Случайная величина.
15. Дискретные и непрерывные случайные величины.
16. Закон распределения вероятностей дискретной случайной величины.
17. Биномиальное распределение случайной величины.
18. Числовые характеристики дискретных случайных величин.
19. Математическое ожидание дискретной случайной величины, его свойства.
20. Дисперсия дискретной случайной величины, его свойства.
21. Среднее квадратическое отклонение дискретной случайной величины.
|
|
|
22. Закон больших чисел.
23. Определение функции распределения вероятностей случайной величины.
24. Свойства функции распределения вероятностей случайной величины.
25. График функции распределения случайной величины.
26. Определение плотности распределения вероятностей непрерывной случайной величины.
27. Вероятность попадания непрерывной случайной величины в заданный интервал.
28. Нахождение функции распределения по известной плотности распределения.
29. Свойства плотности распределения непрерывной случайной величины.
30. Числовые характеристики непрерывной случайной величины.
31. Нормальное распределение непрерывной случайной величины.
32. Числовые характеристики непрерывной случайной величины.
Тема 11. Комплексные числа
Основные понятия
Решение многих задач сводится к решению алгебраических уравнений. Стремление сделать уравнения разрешимыми – одна из главных задач и причин расширения понятия числа. Так, например решение уравнения вида x2 = a на множестве рациональных чисел не имеет решения. Необходимость решения таких уравнений явилось одной из причин введения иррационального числа. Однако и действительных чисел недостаточно для того, чтобы решить любое алгебраическое уравнение. Например, уравнение х2 + 1 = 0 не имеет действительных корней, поэтому приходится расширять множество действительных чисел до нового множества
Корень уравнения х2 + 1 = 0 называется мнимой единицей и обозначается i2 = - 1.
Определение: Комплексным числом 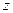 называется выражение вида
называется выражение вида 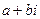 , где
, где 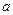 и
и 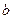 – действительные числа, а символ
– действительные числа, а символ 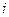 удовлетворяет условию
удовлетворяет условию 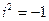 .
.
|
|
|
Определение: Два комплексных числа называются равными, если соответственно равны их действительные части и коэффициенты при мнимой единице.
Определение: Сумма комплексных чисел 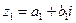 и
и 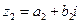 определяется как комплексное число
определяется как комплексное число 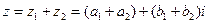 . Вычитание комплексных чисел определяется как операция, обратная сложению:
. Вычитание комплексных чисел определяется как операция, обратная сложению:
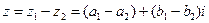
Умножение двух комплексных чисел определяется следующим образом:
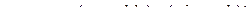
Частным от деления комплексного 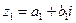 числа на число
числа на число 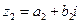 называется комплексное число такое
называется комплексное число такое 
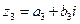 , что
, что 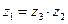 , то есть
, то есть
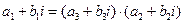 .
.
Таким образом, частное от деления двух комплексных чисел вычисляется по формуле: 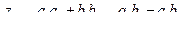 .
.
Тригонометрическая форма комплексного числа: 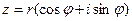 , где
, где
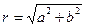 ,
, 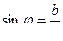 ;
; 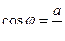 .
.
Показательная форма комплексного числа: 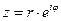 .
.
Пример 1.
Найти сумму, разность, произведение и частное комплексных чисел 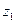 и
и 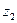 , результат записать в алгебраической, тригонометрической и показательной форме:
, результат записать в алгебраической, тригонометрической и показательной форме: 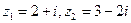
Найдем сумму комплексных чисел: 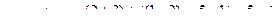 .
.
Найдем разность комплексных чисел: 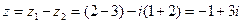 .
.
Найдем произведение комплексных чисел. Комплексные числа перемножаются как двучлены, причем 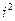 заменяется на - 1.
заменяется на - 1.
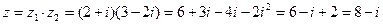
Найдем частное комплексных чисел. Для этого числитель и знаменатель дроби надо умножить на число, сопряженное знаменателю.
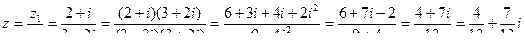
Представим число 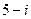 в тригонометрической и показательной форме. Модуль данного числа равен
в тригонометрической и показательной форме. Модуль данного числа равен 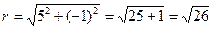 . Данное комплексное число находится в четвертой четверти комплексной плоскости, так как
. Данное комплексное число находится в четвертой четверти комплексной плоскости, так как 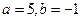 , поэтому
, поэтому 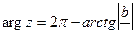 . Следовательно
. Следовательно 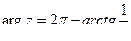 . Запишем число
. Запишем число 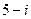 в тригонометрической форме:
в тригонометрической форме: 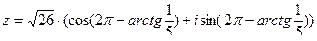 . Записываем число
. Записываем число 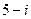 в показательной форме:
в показательной форме: 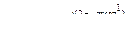 . Аналогично записываются числа
. Аналогично записываются числа 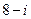 и
и 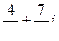 в тригонометрической и показательной формах.
в тригонометрической и показательной формах.
Пример 2.
а) Вычислить: 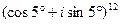
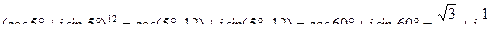
б) Вычислить: 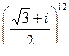
Перепишем данное комплексное число в виде: 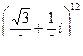 и представим его в тригонометрической форме. Модуль данного числа равен
и представим его в тригонометрической форме. Модуль данного числа равен
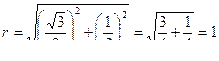 , при вычислении аргумента учитываем, что
, при вычислении аргумента учитываем, что 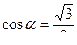 и
и 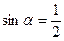 . Значит
. Значит 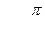 , отсюда
, отсюда
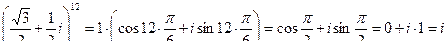
 2020-10-12
2020-10-12 115
115








