Вектори рівні, якщо вони колінеарні, мають однакові напрями і рівні модулі

1 2 3 4 5 6 7

МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ

КРАСНОАРМІЙСЬКИЙ ІНДУСТРІАЛЬНИЙ ІНСТИТУТ

ДЕРЖАВНОГО ВИЩОГО НАВЧАЛЬНОГО ЗАКЛАДУ

«ДОНЕЦЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ»

ВЕКТОРНА АЛГЕБРА

ОПОРНИЙ КОНСПЕКТ ЛЕКЦІЙ

(для студентів усіх форм навчання)

КРАСНОАРМІЙСЬК – 2009

МІНІСТЕРСТВО ОСВІТИ ТА НАУКИ УКРАЇНИ

КРАСНОАРМІЙСЬКИЙ ІНДУСТРІАЛЬНИЙ ІНСТИТУТ

ДЕРЖАВНОГО ВИЩОГО НАВЧАЛЬНОГО ЗАКЛАДУ

«ДОНЕЦЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ»

ВЕКТОРНА АЛГЕБРА

ОПОРНИЙ КОНСПЕКТ ЛЕКЦІЙ

(для студентів усіх форм навчання)

Розглянуто на засіданні кафедри Природничі науки

Протокол № 8 від 29 квітня 2009р.

Затверджено науково – видавничою Дон НТУ

Протокол № 2 від 29 квітня 2009р.

КРАСНОАРМІЙСЬК – 2009

УДК 330.4.

Векторна алгебра. Опорний конспект лекцій. / Укладачі: ст. викл. О.М. Данильчук, ас. М.О. Бабенко – Красноармійськ, Дон НТУ КІІ, Красноармійськ., Видавництво Красноармійського індустріального інституту, 2009. – 35с.

Даний курс лекцій складений відповідно до діючої програми курсу з даної дисципліни і призначений для всіх категорій студентів вузів, як денного так і заочного відділення, які вивчають дану дисципліну в тому чи іншому об’ємі.

Даний конспект лекцій орієнтований на організацію оволодіння даного матеріалу самостійного опрацювання студентів як технічних, так і економічних спеціальностей вищих навчальних закладів. Теоретичний матеріал по всім темам супроводжується малюнками та розгляданням великої кількості прикладів та задач, які подаються в доступній формі.

Укладачі О.М.Данильчук ст.викл.

М.О. Бабенко ас.

Відповідальний за випуск: Я.О. Ляшок, доц. к.т.н.

Рецензент: О.Д.Петренко – доктор фізико – математичних наук, професор кафедри математики Донецького національного технічного університету

@ О.М. Данильчук, ст.викл., М.О. Бабенко, асист.

ЗМІСТ

Вступ.......................................................................................................................6

Лекція 1.

Тема: Вектори, лінійні операції з векторами. Декартові координати вектора і точки.......................................................................................................................7-20

Лекція 2.

Тема: Скалярний, векторний і мішаний добутки векторів. Властивості та застосування в задачах.................................................................................................21-33

Список рекомендованої літератури.........................................................................34

ВСТУП

Сучасний рівень і темпи розвитку суспільства висувають потреби не тільки мати науковий потенціал в обраній діяльності, але й ефективно застосовувати здобуті знання для розв’язку проблем, що виникають в їх практичній діяльності.

Головна мета викладання вищої математики – дати студентам фундаментальні знання з математики, щоб у подальшому вони могли засвоювати спеціальні дисципліни, які базуються на математичних поняттях. При цьому значна увага приділяється виробленню практичних навичок у процесі розв’язання конкретних задач, а також навчанню застосовувати математичні методи для дослідження реальних чи то економічних чи технічних процесів і прийняття оптимальних рішень розв’язку.

Метою запропонованих лекцій є стисле та послідовне подання основного курсу вищої математики по темі „Векторна алгебра” яке адаптоване для вищих навчальних закладів економічного та технічного профілю.

Опорний конспект лекцій є наочним відображенням програмного матеріалу з дисципліни „Вища математика” і може бути використаний для вузівського супроводження лекцій з усіх тем курсу. Відомо, що новий навчальний матеріал засвоюється студентами значно легше, якщо він супроводжується достатньо великою малюнків, що ілюструють їх розв’язання.

Систематичне та якісне подання основних тем сприяє свідомому засвоєнню курсу студентами, як денної так і заочної форми навчання. Опорний конспект лекцій призначений як для самостійної роботи студентів так і для підготовки до складання заліків та іспитів(МК).

Під час роботи з опорним конспектом студентам необхідно використовувати основну і додаткову літературу, а набуті теоретичні знання закріплювати розв’язанням практичних задач і прикладів, які теж можна знайти у рекомендованих збірниках задач. Доцільно також опрацьовувати методичні розробки кафедри з даної дисципліни.

Лекція 1.

Тема: Вектори, лінійні операції з векторами. Декартові координати вектора і точки.

План лекції

Скалярні і векторні величини. Вектори. Колінеарні і компланарні вектори. Рівність векторів. Додавання векторів, Множення вектора на число.
Визначення положення точки радіусом - вектором. Поділ відрізка уданому відношенні.
Лінійна залежність векторів. Умова колінеарності двох векторів. Розкладання вектора за двома векторами. Умова компланарності трьох векторів. Розкладання вектора за трьома векторами.
Координати на прямій. Координати на площині. Координати у просторі.
Координати точки поділу. Координати вектора, що задано двома точками. Ознака колінеарності двох векторів. Ознака компланарності трьох векторів.

1. У повсякденній практиці ми маємо справу з величинами двох видів. Одні з цих величин такі, як температура, час, маса, довжина, площа, робота тощо можна визначити одним числовим значенням, інші ж величини, такі, як сила, швидкість, прискорення тощо можна визначити тільки тоді, коли відомо не тільки їх числове значення, а й напрям у просторі. Величини першого виду називають скалярними величинами або скалярами. Величини другого виду називають векторними величинами.

Кожну векторну величину геометрично можна зобразити напрямленим прямолінійним відрізком - вектором - довжина якого дорівнює числовому значенню векторної величини {у вибраному масштабі) і напрям співпадає з напрямом цієї величини.

Вектор визначають двома точками: перша - це початок його, друга - кінець; додатний напрям вектора - від початку до кінцевої точки, наприклад, вектор має початок у точці А і кінець у точці В, стрілка вказує напрям вектора.

Якщо початок і кінець вектора співпадають, то вектор називають нульовим (нуль-вектор).

Два ненульових вектори і називають колінеарними, якщо прямі AB і CD паралельні або співпадають.

Вектори називають компланарними, якщо вони лежать в одній або паралельних площинах.

Довжина, або модуль, вектора - це відстань між його початком А і кінцем (довжина відрізка АВ). Для модуля вектора використовують позначення або Вектор, довжина якого дорівнює одиниці, називають одиничний вектор або орт.

Вектори рівні, якщо вони колінеарні, мають однакові напрями і рівні модулі.

На рис.1, де АВСD є паралелограм, зображено рівні вектори = . Вектори і не рівні. Хоч ці вектори і колінеарні, і мають рівні модулі, але вони протилежно напрямлені. ,

Рис. 1

Вектори можна додавати, віднімати, множити на число.

Додавання двох векторів - це операція побудови за двома векторами і третього вектора - вектора суми .

Рис. 2

Цю побудову виконуємо так: 1) з довільної точки О відкладаємо вектор ; 2) з його кінця А відкладаємо вектор ; 3) з'єднаємо початок О першого вектора з кінцем В другого. Знайдений в результаті цієї побудови вектор = 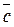називають вектором-сумою векторів і .

Отже, сумою векторів і є вектор, що сполучає початок вектора з кінцем вектора за умови, що вектор відкладено від кінця вектора .

Це правило називають правилом трикутника.

Для позначення операції додавання векторів вживають звичайні алгебраїчні символи:

Іншим способом побудови суми двох векторів є так зване правило паралелограма: якщо вектори і відкласти від спільного початку О (рис. 3) і на них побудувати паралелограм, то сума і є вектор , що виходить з того ж початку О іспівпадає з діагоналлю паралелограма.

Рис. 3

З рис. З видно, що це правило є наслідком правила трикутника.

Розглядаючи фігури ОАС і ОВС (рис. 4), знайдемо, що

, тобто сума двох векторів не залежить від порядку доданків.

Послідовно використовуючи правило трикутника ми можемо побудувати суму будь-якого числа довільно розміщених у просторі векторів. Сумою цих векторів буде вектор, початком якого є початок першого вектора і кінцем - кінець останнього вектора - доданка.

Якщо кінець останнього вектора - доданка співпадає з початком першого, то сумою векторів буде нульовий вектор.

Різницею двох векторів і є вектор , що у сумі з вектором дає вектор :

якщо .

З означення видно, що для побудови різниці потрібно віднести вектори і до спільного початку О (рис. 4) і провести вектор

Рис. 4

від кінця В вектора - від'ємника до кінця А вектора зменшуваного; цей вектор і є шукана різниця :

Зауважимо, що у паралелограмі, побудованому на векторах і одна з діагоналей є сума векторів і , а друга їх різниця (рис.4).

Добутком вектора на число λ≠0є вектор:

1)колінеарний вектору ,

2)модуль (довжина) якого дорівнює добутку модулів числа λ і вектора ;

3)напрям його співпадає з напрямом вектора , якщо λ>0 або протилежний йому, якщо λ <0.

Ділення вектора на число просто звести до операції множення: щоб поділити вектор на число λ≠0, досить помножити цей вектор на обернене число , тобто

Зокрема, одиничний вектор, або орт , відповідний вектору , дістанемо з вектора , поділивши останній на його модуль , тобто помноживши на :

Добуток вектора на число має такі властивості:

1. ,

2. ,

3. .

2. Виберемо у просторі довільну точку О. Будемо називати її початком або полюсом. Тоді положення будь-якої точки М простору можна однозначно визначити вектором , початок якого є фіксована точка - полюс О, а кінець - точка М. Цей вектор називають радіус- вектор точки М відносно О і позначають :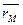

Рис. 5

Якщо задано дві точки М₁і М₂, що визначають вектор (рис.5), то , тобто довільний вектор дорівнює різниці радіуса вектора його кінця і радіуса вектора його початку.

Розглянемо тепер задачу знаходження радіуса-вектора точки М, що лежить на прямій М₁М₂ і ділить відрізок у заданому відношенні λ (λ = М₁ М: ММ₂).

Очевидно, , але то . Звідси

(1.1)

В окремому випадку, коли М є середина відрізка і формула (1.1) набуває вигляду

(1.2)

3. Введемо тепер поняття про лінійну залежність векторів.

Вектори називають лінійно залежними, якщо існують такі числа α,β,γ,...,δ, з яких хоча б одне було відмінне від нуля, при яких лінійна комбінація цих векторів з коефіцієнтами α,β,γ,...,δ дорівнює нуль – вектору

Розглянемо спочатку два лінійно залежних вектори і . З означення лінійної залежності маємо

, (1.3)

при цьому, хоча б один з коефіцієнтів а і β, наприклад,а не дорівнює нулеві. Тоді знайдемо

Ця рівність означає, що вектори і колінеарні.

У випадку лінійної залежності трьох векторів маємо:

(1.4)

Якщо а ≠0, то

або

де

, .

Лінійна комбінація векторі є вектор, що лежить у площині, в якій лежать вектори і . Тому і рівний йому вектор буде паралельний цій площині або лежати в ній. Отже, вектори , , компланарні.

Це означає, що у випадку трьох компланарних векторів один з них можна розкласти за двома іншими неколінеарними векторами.

Дійсно, нехай маємо компланарні вектори , , з яких і неколінеарні. Відкладаємо від спільного початку О (рис. 6) і позначимо .

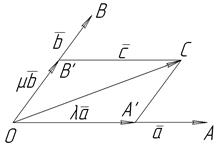
Рис. 6

Точки О,А,В,С знаходяться в одній площині. Через кінець С вектора проведемо прямі СА' і СВ' паралельно прямим ОА і ОВ відповідно. Дістанемо паралелограм ОА'СВ', діагоналлю ОС якого є вектор . Отже,

Вектори і колінеарні векторам і . Тому

де

і - відповідні відношення модулів цих пар колінеарних векторів.

Звідси

(1.5)

Покажемо тепер, що у випадку трьох некомпланарних векторів , , будь-який четвертий вектор можна представити у вигляді

(1.6)

Для цього віднесемо вектори а,b,с і d до спільного початку О (рис. 7)

Рис. 7

і позначимо , , . Через кінець D вектора проведемо площини паралельно площинам ОАВ, ОВС і ОСА. Отримаємо паралелепіпед, діагональ якого є вектор , а ребра колінеарні відповідно векторам , , . Діагональ замикає ламану ОА'ND. Тому згідно з правилом додавання векторів маємо

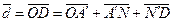
Оскільки ; ; колінеарні відповідно векторам , , ., то, припустивши, що , , , дістанемо шукану залежність:

4. Координати на прямій. Розглянемо довільну пряму і виберемо на ній додатний напрям, фіксовану точку О (початок) і масштабну одиницю. Це - координатна вісь.

Координатну вісь можна також визначити віднесеним до її початку О одиничним вектором ї. Положення довільної точки М(r) на цій вісі

Рис. 8

визначимо її радіусом-вектором . Вектор колінеарний орту незалежно від положення точки М на вісі, а тому його завжди можна однозначно виразити через ірівністю

(1.6) де число х є відношення модулів колінеарних векторів та .Це число буде додатним (х>0), від'ємним (х<0) якщо ці напрями протилежні, і х= 0, якщо точка М співпадає з точкою О.

Рівність (1.6) встановлює взаємно однозначну відповідність між радіусом-вектором точок координатної вісі і дійсними числами.

Тому число г називають координатою вектора відносно базису (О; ). Положення точки М також буде визначено числом х- довжиною (модулем) вектора . Це число називають координатою точки М і позначають М(х).

Координати на площині. Щоб ввести поняття координат вектора і точки на площині побудуємо в ній так званий координатний базис. Для цього від довільно вибраної точки О в площині відкладемо упорядковану пару взаємно перпендикулярних одиничних векторів (ортів) та . Вектор і, що визначає координатну вісь Ох (вісь абсцис), розташуємо горизонтально і напрям його виберемо зліва направо, а вектор , що визначає координатну вісь Оу (вісь ординат),- вертикально і напрям його

Рис.9

виберемо знизу вгору (рис. 9). Тепер кожний вектор площини, а отже і радіус - вектор довільної точки М можна розкласти за базисними векторами та тобто представити у вигляді

(1.7)

З (1.7) видно, що кожному вектору площини відповідають два упорядкованих числа х і у - коефіцієнти при першому і другому базисних векторах, і навпаки, якщо задано два упорядкованих числа х і у, то можна однозначно побудувати відповідний їм вектор .

Числа х і у називають координатами вектора у вибраному базисі (О; i; j ).

Положення довільної точки М на площині визначає її радіус - вектор Тому кожній точці М можна поставити відповідну упорядковану пару чисел х і у. Ц\ числа називають координатами точки М і записують у вигляді М(х,у).

Координати у просторі. Назвемо координатним базисом у просторі віднесену до вибраної точки О (початок координат) упорядковану трійку перпендикулярних некомпланарних векторів і , . Орти і лежать в горизонтальній площині і визначають відповідно вісь Ох- вісь абсцис і вісь Оу- вісь ординат. Орт

Рис. 10

проведено перпендикулярно до площини, в якій лежать орти і і визначає вісь О z –вісь аплікат (додатний напрям - вгору).

Кожна пара з трійки векторів визначає площину, яку називають координатна площина.

Всі точки координатної площини, що визначено ортами і (площина Оу z ), мають координату х-0, ортами і (площина Ох z ) - у = 0, а ортами і (площина Оху)- z = 0.

Розклад довільного вектора за базисними векторами

(1.8)

однозначно визначає для кожного вектора три упорядковані числа х, у, z - координати вектора у вибраному базисі і , .

Положення кожної точки М простору визначає ЇЇ радіус - вектор .Цей вектор цілком визначено його координатами { х, у, z }. Тому і довільній точці М можна поставити взаємно однозначну відповідність упорядковану трійку чисел х, у, z, які будемо називати координатами точки М і записувати М{х, у, z).

5. Розглянемо тепер дії з векторами у координатній формі.

Якщо у просторі задано два вектори їх координатами

то на підставі алгебраїчних властивостей додавання, віднімання і множення вектора на число отримаємо

(1.9)

(1.10)

тобто, координати суми (різниці) двох векторів дорівнюють сумам (різницям) відповідних координат цих векторів, а координати добутку вектора на число дорівнюють добуткам відповідних координат вектора на це число.

Узагальненням цих результатів є правило знаходження координат лінійної комбінації векторів.

Якщо у просторі

(1.11)

і то

( 1.12 )

Для площини формули, відповідні формулам (1.9) - (1.12), отримаємо, взявши координати z = 0, а для прямої -у=0, z = 0.

Знайдемо координату точки М{х, у, z ), що ділить відрізок М₁М₂ між точками М₁ (х₁; у₁; z₁) і М₂(х₂,у₂, z ₂) у відношенні З формули (1.1)

(1.13)

маємо

(1.14)

Як окремий випадок для дістанемо формули, що визначають координати середини відрізка М₁М₂:

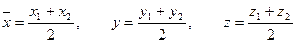
Тепер знайдемо координати х, у, zвектора , початком якого є точка М₁ (х₁; у₁; z₁), а кінцем - точка М₂(х₂,у₂, z ₂). із-за того, що отримаємо

Як відомо, між колінеарними векторами існує лінійна залежність

Звідси

або

(1.15)

Це означає, що координати колінеарних векторів пропорційні між собою.

Між компланарними векторами , існує лінійна залежність:

Векторна рівність еквівалентна трьом різностям:

Ця система рівнянь відносно лінійна і однорідна. А для того, щоб вона мала ненульовий розв'язок, необхідно і достатньо, щоб визначник системи дорівнював нулеві: