Задачи
5.1. Сколько существует абстрактных эйлеровых графов с 5 вершинами?
5.2. Граф 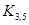 нужно превратить в эйлеров, изменяя (удаляя и добавляя) ребра. Каково
нужно превратить в эйлеров, изменяя (удаляя и добавляя) ребра. Каково
наименьшее число изменений, если разрешается а) только удалять ребра; б) только
добавлять ребра; в) и удалять, и добавлять?
5.3. Проследите работу алгоритма построения эйлерова цикла на графе 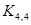 . Вершины
. Вершины
одной доли имеют номера 1-4, другой – номера 5-8, старт в вершине1. Всякий раз,
когда имеется несколько непройденных ребер, по которым можно продолжить
движение, выбирается то из них, которое ведет в вершину с наименьшим номером.
5.4. Алгоритм построения эйлерова цикла применяется к графу 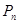 . Каков будет ответ
. Каков будет ответ
(содержимое стека С в конце работы алгоритма)?
5. 5. Что нужно изменить в алгоритме построения эйлерова цикла, чтобы получился
алгоритм построения эйлерова пути в графе с двумя вершинами нечетной степени?
5.6. С помощью графа де Брейна найдите последовательность де Брейна 1) порядка 4 для
двухбуквенного алфавита; 2) порядка 2 для четрехбуквенного алфавита.
|
|
|
5.7. Сколько существует абстрактных графов с 5 вершинами, имеющих гамильтонов
цикл?
5.8. В каких из следующих графов имеется гамильтонов цикл?
1) 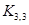 ; 2)
; 2) 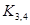 ; 3)
; 3)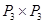 ; 4)
; 4) 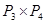 ; 5)
; 5) 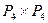 .
.
5.9. При каких p и q в графе 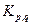 имеется а) гамильтонов цикл? Б) гамильтонов путь?
имеется а) гамильтонов цикл? Б) гамильтонов путь?
5.10. При каких n существует гамильтонов цикл в графе а)  ; б)
; б) 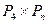 ?
?
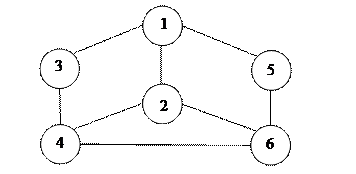
5.11. Постройте дерево путей для графа, изображенного на рисунке а) с корнем в
вершине 1; б) с корнем в вершине 2.
5.12. Сколько листьев будет в дереве путей для графа 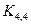 ?
?
5.13. Найдите гамильтонов путь в графе  .
.
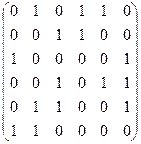
5.26. Найдите гамильтонов путь в турнире, заданном матрицей смежности:
5.15. Сколько в полном графе 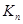 имеется подграфов, изоморфных а)
имеется подграфов, изоморфных а) 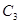 ; б)
; б)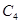 ;
;
в)  ,
, 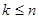 ?
?
5.16. Операция сложения графов по модулю 2 может быть распространена на графы с
разными множествами вершин следующим образом: если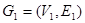 ,
,
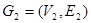 , то
, то 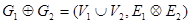 . Можно ли с помощью этой операции, а
. Можно ли с помощью этой операции, а
также удаления и добавления изолированных вершин и переименования вершин
получить а) 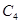 из
из 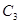 ; б)
; б) 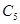 из
из 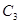 ; в)
; в) 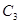 из
из 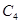 ; г)
; г) 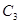 из
из 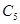 ?
?
5.17. Связный граф имеет 10 вершин, 4 из них имеют степень 6, остальные – степень 3.
Чему равно цикломатическое число этого графа?
5.18. Постройте фундаментальные циклы для графа 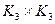 относительно каркаса,
относительно каркаса,
полученного с помощью а) поиска в глубину; б) поиска в ширину. Выразите границу
внешней грани как сумму базисных циклов.
5.19. Какова будет суммарная длина фундаментальных циклов, построенных с помощью
поиска в ширину для графа а) 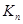 ; б)
; б) 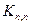 ?
?
|
5.20. Сколько различных разрезов имеется а) у связного графа с n вершинами;
б) у графа с k компонентами и n вершинами?
5.21. Найдите базис циклов по матрице инцидентности для графа, показанного на
|
|
|
рисунке.
5.22*. Модифицируйте алгоритм построения эйлерова цикла так, чтобы не требовалась
предварительная проверка четности степеней. Существование вершины нечетной
степени должно обнаруживаться по ходу работы алгоритма.
5.23*. Докажите, что при любом 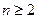 в графе
в графе  существует гамильтонов цикл.
существует гамильтонов цикл.
5.24*. Разработайте алгоритм построения дерева путей и поиска гамильтонова цикла.
5.25*. Докажите, что в любом сильно связном турнире имеется гамильтонов цикл.
5.26.* Разработайте алгоритм построения базиса циклов на основе поиска в ширину.
Здесь рассмотрим три задачи, тесно связанные между собой.
Независимым множеством вершин графа называется любое множество попарно не смежных вершин, т.е. множество вершин, порождающее пустой подграф. Независимое множество называется наибольшим, если оно содержит наибольшее количество вершин. Число вершин в наибольшем независимом множестве графа G обозначается через 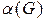 и называется числом независимости графа. Задача о независимом множестве состоит в нахождении наибольшего независимого множества.
и называется числом независимости графа. Задача о независимом множестве состоит в нахождении наибольшего независимого множества.
Кликой графа называется множество вершин, порождающее полный подграф, т.е. множество вершин, каждые две из которых смежны. Число вершин в клике наибольшего размера называется кликовым числом графа и обозначается через 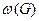 . Очевидно, задача о независимом множестве преобразуется в задачу о клике и наоборот простым переходом от данного графа G к дополнительному графу
. Очевидно, задача о независимом множестве преобразуется в задачу о клике и наоборот простым переходом от данного графа G к дополнительному графу 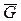 , так что
, так что  .
.
Вершинное покрытие графа – это такое множество вершин, что каждое ребро графа инцидентно хотя бы одной из этих вершин. Наименьшее число вершин в вершинном покрытии графа G обозначается через 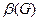 и называется числом вершинного покрытия графа.
и называется числом вершинного покрытия графа.
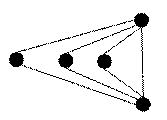
В графе на рисунке 9 наибольшим независимым множеством является множество {1,3,4,7}, наибольшей кликой – множество {2,3,5,6}, наименьшим вершинным покрытием – множество {2,5,6}.

Рис. 9.
Между задачами о независимом множестве и о вершинном покрытии имеется простая связь.
Теорема о независимом множестве и вершинном покрытии. Пусть G – граф с множеством вершин V. Множество 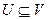 является вершинным покрытием графа G тогда и только тогда, когда
является вершинным покрытием графа G тогда и только тогда, когда 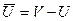 – независимое множество.
– независимое множество.
Из этой теоремы следует, что 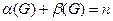 для любого графа G с n вершинами.
для любого графа G с n вершинами.
Итак, все три задачи тесно связаны друг с другом и алгоритм для решения одной из них легко преобразуется в алгоритм решения другой. В то же время эти задачи относятся к категории неподдающихся, так что все известные алгоритмы получения их точного решения имеют переборный характер и требуют во многих случаях много времени даже для не очень больших графов. Для того, чтобы можно было решить задачу за реальное время, приходится ослаблять требования, например, искать не точное, а достаточно хорошее или приемлемое для практики решение (например, не обязательно наибольшее, но достаточно большое независимое множество). Алгоритмы, реализующие такой подход, основываются на разнообразных интуитивных идеях о том, как найти хорошее решение. Такие идеи называют эвристиками, а основанные на них алгоритмы – эвристическими алгоритмами. Иногда удается оценить точность приближения, тогда говорят о приближенном алгоритме. Рассмотрим некоторые точные, эвристические и приближенные алгоритмы для задач о независимом множестве и вершинном покрытии.
Пусть G – граф, в котором требуется найти наибольшее независимое множество. Выберем в нем произвольную вершину а, не являющуюся изолированной и рассмотрим две возможности – эта вершина принадлежит искомому множеству Х или не принадлежит ему. Если не принадлежит, то Х является независимым множеством графа, получаемого удалением вершины а из графа G. Обозначим этот граф через 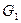 . Если же а принадлежит Х, то никакая вершина, смежная с a, не принадлежит X. В этом случае множество Х является независимым множеством графа, получающийся удалением из G всех вершин, смежных с a. Обозначим этот граф через
. Если же а принадлежит Х, то никакая вершина, смежная с a, не принадлежит X. В этом случае множество Х является независимым множеством графа, получающийся удалением из G всех вершин, смежных с a. Обозначим этот граф через 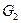 . В графе
. В графе 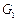 вершин меньше, чем в графе G, а так как вершина а не изолированная, то в графе
вершин меньше, чем в графе G, а так как вершина а не изолированная, то в графе 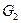 их тоже меньше. Таким образом, задача о независимом множестве для графа G свелась к решению той же задачи для двух графов меньшего размера. Это приводит к рекуррентному соотношению для числа независимости:
их тоже меньше. Таким образом, задача о независимом множестве для графа G свелась к решению той же задачи для двух графов меньшего размера. Это приводит к рекуррентному соотношению для числа независимости:
|
|
|
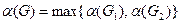
и к рекурсивному алгоритму для нахождения наибольшего независимого множества графа G: найдем наибольшее независимое множество 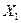 графа
графа 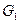 , затем наибольшее независимое множество
, затем наибольшее независимое множество 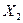 графа
графа 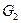 и выберем большее из этих двух множеств. Процесс решения можно изобразить в виде бинарного дерева (его называют деревом подзадач, деревом вариантов, деревом решений). Корнем дерева служит граф G, его двумя сыновьями – графы
и выберем большее из этих двух множеств. Процесс решения можно изобразить в виде бинарного дерева (его называют деревом подзадач, деревом вариантов, деревом решений). Корнем дерева служит граф G, его двумя сыновьями – графы 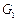 и
и 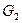 . Чтобы не путать вершины дерева и вершины графа, вершины дерева будем называть узлами. Узел, не являющийся листом, называется внутренним узлом. Каждому внутреннему узлу дерева соответствует некоторый граф H и некоторая вершина этого графа x. Вершину x можно выбирать произвольно, но она не должна быть изолированной вершиной графа H. Внутренний узел имеет двух сыновей – левого и правого. Левому сыну соответствует подграф графа H, получаемый удалением вершины x, а правому – подграф, получаемый удалением всех вершин, смежных с x. Листьям соответствуют подграфы, не имеющие ребер, то есть подграфы, у которых все вершины изолированные. Множества вершин этих подграфов – это независимые множества исходного графа.
. Чтобы не путать вершины дерева и вершины графа, вершины дерева будем называть узлами. Узел, не являющийся листом, называется внутренним узлом. Каждому внутреннему узлу дерева соответствует некоторый граф H и некоторая вершина этого графа x. Вершину x можно выбирать произвольно, но она не должна быть изолированной вершиной графа H. Внутренний узел имеет двух сыновей – левого и правого. Левому сыну соответствует подграф графа H, получаемый удалением вершины x, а правому – подграф, получаемый удалением всех вершин, смежных с x. Листьям соответствуют подграфы, не имеющие ребер, то есть подграфы, у которых все вершины изолированные. Множества вершин этих подграфов – это независимые множества исходного графа.
Дерево решений может быть очень большим. Например, для графа 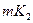 в этом дереве будет
в этом дереве будет 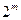 листьев. Для нахождения наибольшего независимого множества не обязательно строить все дерево полностью, а достаточно обойти его в том или ином порядке, запоминая на каждом шаге только небольшую часть информации об устройстве этого дерева. Можно, например, применить поиск в глубину для обхода дерева: сначала пройти от корня до некоторого листа, затем вернуться к предку этого листа и искать следующий лист, и т.д.
листьев. Для нахождения наибольшего независимого множества не обязательно строить все дерево полностью, а достаточно обойти его в том или ином порядке, запоминая на каждом шаге только небольшую часть информации об устройстве этого дерева. Можно, например, применить поиск в глубину для обхода дерева: сначала пройти от корня до некоторого листа, затем вернуться к предку этого листа и искать следующий лист, и т.д.
|
|
|
Рассмотрим две простые эвристики для задачи о независимом множестве.
Одна из эвристических идей состоит в том, чтобы рассмотреть только один путь от корня до листа в дереве решений в надежде, что этому листу соответствует достаточно большое независимое множество. Для выбора этого единственного пути могут применяться разные соображения. В дереве решений, описанном выше, у каждого внутреннего узла имеются два сына. Одному из них соответствует подграф, получающийся удалением некоторой произвольно выбранной вершины a, а другому – подграф, получающийся удалением окрестности этой вершины. Чтобы вместо дерева получился один путь, достаточно каждый раз выполнять какую-нибудь одну из этих двух операций. Рассмотрим оба варианта.
Допустим, мы решили каждый раз удалять выбранную вершину. Эти удаления производятся до тех пор, пока не останется граф без ребер, т.е. независимое множество. Оно и принимается в качестве решения задачи. Для полного описания алгоритма необходимо еще сформулировать правило выбора активной вершины a. Мы хотим получить граф без ребер, в котором было бы как можно больше вершин. Чем меньше вершин будет удалено, тем больше их останется. Значит, цель – как можно быстрее удалить все ребра. Кажется, мы будем двигаться в нужном направлении, если на каждом шаге будем удалять наибольшее возможное на этом шаге число ребер. Это означает, что в качестве активной вершины всегда нужно выбирать вершину наибольшей степени. Другой вариант – каждый раз удалять окрестность активной вершины a. Это повторяется до тех пор, пока оставшиеся вершины не будут образовывать независимого множества. Удаление окрестности вершины a равносильно тому, что сама эта вершина включается в независимое множество, которое будет получено в качестве ответа. Так как мы хотим получить в итоге как можно большее независимое множество, следует стараться удалять на каждом шаге как можно меньше вершин. Это означает, что в качестве активной вершины всегда нужно выбирать вершину наименьшей степени.
Имеется немало графов, для которых каждая из этих эвристик дает близкое к оптимальному, а иногда и оптимальное решение. Но, как это обычно бывает с эвристическими алгоритмами, можно найти примеры графов, для которых найденные решения будут весьма далеки от оптимальных. Рассмотрим граф 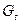 , у которого множество вершин V состоит из трех частей:
, у которого множество вершин V состоит из трех частей: 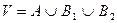 , причем
, причем 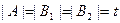 , A является независимым множеством, каждое из множеств
, A является независимым множеством, каждое из множеств 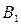 ,
,  – кликой, и каждая вершина из множества A смежна с каждой вершиной из множества
– кликой, и каждая вершина из множества A смежна с каждой вершиной из множества 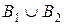 . Этот граф можно представить формулой
. Этот граф можно представить формулой  . Степень каждой вершины из множества A в этом графе равна
. Степень каждой вершины из множества A в этом графе равна 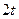 , а степень каждой вершины из множества
, а степень каждой вершины из множества 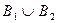 равна
равна 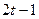 . Первый алгоритм, выбирающий вершину наибольшей степени, будет удалять вершины из множества A до тех пор, пока не удалит их все. После этого останется граф, состоящий из двух клик, и в конечном итоге будет получено независимое множество из двух вершин. Второй алгоритм на первом шаге возьмет в качестве активной одну из вершин множества
. Первый алгоритм, выбирающий вершину наибольшей степени, будет удалять вершины из множества A до тех пор, пока не удалит их все. После этого останется граф, состоящий из двух клик, и в конечном итоге будет получено независимое множество из двух вершин. Второй алгоритм на первом шаге возьмет в качестве активной одну из вершин множества 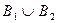 и удалит всю ее окрестность. В результате получится граф, состоящий из этой вершины и клики, а после второго шага получится независимое множество, состоящее опять из двух вершин. Итак, при применении к этому графу любой из двух эвристик получается независимое множество из двух вершин. В то же время в графе имеется независимое множество A мощности t.
и удалит всю ее окрестность. В результате получится граф, состоящий из этой вершины и клики, а после второго шага получится независимое множество, состоящее опять из двух вершин. Итак, при применении к этому графу любой из двух эвристик получается независимое множество из двух вершин. В то же время в графе имеется независимое множество A мощности t.
Рассмотрим другой способ организации перебора для получения точного решения Он использует алгебраические преобразования. Для его описания удобнее рассмотреть задачу о вершинном покрытии. Пусть 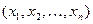 – характеристический вектор искомого множества Х. Это множество должно быть вершинным покрытием, т.е. хотя бы одна из двух вершин каждого ребра должна принадлежать множеству Х. Это означает, что для каждого ребра
– характеристический вектор искомого множества Х. Это множество должно быть вершинным покрытием, т.е. хотя бы одна из двух вершин каждого ребра должна принадлежать множеству Х. Это означает, что для каждого ребра 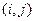 дизъюнкция
дизъюнкция 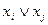 должна быть равна 1. Значит, должно выполняться равенство
должна быть равна 1. Значит, должно выполняться равенство
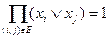 ,
,
где Е – множество ребер графа, а П обозначает конъюнкцию. Формула в левой части равенства – конъюнктивная нормальная форма. Если раскрыть скобки то получится дизъюнктивная нормальная форма, каждое слагаемое которой представляет некоторое вершинное покрытие графа – слагаемое 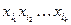 представляет вершинное покрытие, состоящее из вершин с номерами
представляет вершинное покрытие, состоящее из вершин с номерами 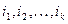 . Остается выбрать слагаемое с наименьшим числом сомножителей. К сожалению, при раскрытии скобок могут получаться очень длинные формулы, даже при применении известных упрощающих преобразований вроде закона поглощения.
. Остается выбрать слагаемое с наименьшим числом сомножителей. К сожалению, при раскрытии скобок могут получаться очень длинные формулы, даже при применении известных упрощающих преобразований вроде закона поглощения.
Рассмотрим еще один простой приближенный алгоритм для задачи о вершинном покрытии.
Работа алгоритма начинается с создания пустого множества X и состоит в выполнении однотипных шагов, в результате каждого из которых к множеству X добавляются новые вершины. Допустим, перед очередным шагом имеется некоторое множество вершин X. Если оно покрывает все ребра (т.е. каждое ребро инцидентно одной из этих вершин), то процесс заканчивается и множество X принимается в качестве искомого вершинного покрытия. В противном случае выбирается какое-нибудь непокрытое ребро 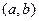 , и вершины a и b добавляются к множеству X.
, и вершины a и b добавляются к множеству X.
Для полного описания алгоритма нужно бы еще сформулировать правило выбора ребра 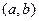 . Однако для оценки степени приближения, которая будет сейчас получена, это не имеет значения. Можно считать, что какое-то правило выбрано.
. Однако для оценки степени приближения, которая будет сейчас получена, это не имеет значения. Можно считать, что какое-то правило выбрано.
Обозначим через 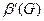 мощность вершинного покрытия, которое получится при применении этого алгоритма к графу G, и докажем, что
мощность вершинного покрытия, которое получится при применении этого алгоритма к графу G, и докажем, что 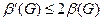 . Иначе говоря, полученное с помощью этого алгоритма решение не более чем в два раза отличается от оптимального.
. Иначе говоря, полученное с помощью этого алгоритма решение не более чем в два раза отличается от оптимального.
Действительно, допустим, что до окончания работы алгоритм выполняет k шагов, добавляя к множеству X вершины ребер 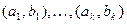 . Тогда
. Тогда 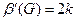 . Никакие два из этих k ребер не имеют общей вершины. Значит, чтобы покрыть все эти ребра, нужно не меньше k вершин. Следовательно,
. Никакие два из этих k ребер не имеют общей вершины. Значит, чтобы покрыть все эти ребра, нужно не меньше k вершин. Следовательно, 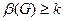 и
и 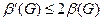 .
.
 2014-02-04
2014-02-04 1537
1537








