Паросочетания и реберные покрытия

Паросочетанием в графе называется множество ребер, попарно не имеющих общих вершин. Задача о паросочетании состоит в том, чтобы в данном графе найти паросочетание с наибольшим числом ребер. Это число для графа G будем обозначать через 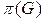. Реберным покрытием графа называется такое множество ребер, что всякая вершина графа инцидентна хотя бы одному из этих ребер. Наименьшее число ребер в реберном покрытии графа G обозначим через 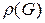. Заметим, что реберное покрытие существует только для графов без изолированных вершин.

Между задачами о паросочетании и о реберном покрытии имеется тесная связь, подобно связи между задачами о независимом множестве (паросочетание называют иногда независимым множеством ребер) и о вершинном покрытии. Количественно эта связь выражается следующим образом.

Теорема 1. Для любого графа G с n вершинами, не имеющего изолированных вершин, справедливо равенство .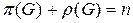

Из решения одной задачи легко получить решение другой. Пусть М – наибольшее паросочетание в графе G, не имеющем изолированных вершин. Для каждой вершины, не принадлежащей никакому ребру паросочетания, выберем какое-нибудь ребро, инцидентное этой вершине и добавим все выбранные ребра к множеству М. Полученное множество ребер будет наименьшим реберным покрытием. Обратно, пусть C – наименьшее реберное покрытие графа G. Тогда в подграфе, образованном ребрами этого покрытия, каждая компонента связности является звездой (звезда – полный двудольный граф, у которого одна доля состоит из одной вершины). Выбрав по одному ребру из каждой компоненты, получим наибольшее паросочетание.

Несмотря на такое сходство между “вершинными” и “реберными” вариантами независимых множеств и покрытий, имеется кардинальное различие в сложности соответствующих экстремальных задач. “Вершинные” задачи относятся кразряду неподдающихся, для реберных же известны полиномиальные алгоритмы.