Основные понятия и определения. Системы линейных уравнений представляют один из важнейших разделов линейной алгебры

Система линейных уравнений.

Системы линейных уравнений представляют один из важнейших разделов линейной алгебры. Они являются одним из основных инструментов моделирования экономических процессов.

Цель - обобщение понятия системы линейных уравнений (в том числе, когда число уравнений m не совпадает с числом неизвестных n); знакомство с матричной формой записи системы линейных уравнений.

Задача - знакомство с различными способами решения систем (преимущества и недостатки каждого из способов). В результате изучения темы студент должен уметь ответить на вопросы:

а) совместна система или нет;

б) уметь решить любым способом, если она совместна.

3.2.1. Основные понятия и определения

3.2.2. Системы n линейных уравнений с n переменными. Метод обратной матрицы и формулы Крамера.

3.2.3. Метод Гаусса.

3.2.4. Системы m линейных уравнений с n переменными. Метод последовательного исключения неизвестных.

Система m линейных уравнений с n переменными имеет вид:

a₁₁x₁+a₁₂x₂+a₁₃x₃+…+a_1jx_j+ …+a_1nx_n =b₁

a₂₁x₁+ a₂₂x₂+a₂₃x₃+…+a_2jx_j+ …+a_2nx_n =b₂

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - (3.2.1)

a_i1x₁+ a_i2x₂ +a_i3x₃+… +a­_ijx_j+…+a_inx_n =b_i

- - - - - - - - - - - - - - - - - - - - - - - - - - - - -

a_m1x₁+a_m2x₂+a_m3x₃+…+a_mjx_j+…a_mnx_n =b_m

где a­_ij – постоянные числа, называемые коэффициентами системы, b_i – постоянные числа, называемые свободными членами (i=1,m, j= ).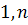

В краткой форме систему (3.2.1) можно записать в форме следующим образом: _n

∑ a­_ijx_j = b_i, (1≤i<m)

_j=1

Совокупность чисел (x₁₀, x₂₀, …x_no) называется решением системы (3.2.1), если после подстановки в каждое уравнение системы обращает его в верное равенство.

Система уравнений называется совместной, если она имеет хот бы одно решение и несовместной, если она не имеет решений.

Две системы называются равносильными (эквивалентными), если решение одной из них является решением другой и наоборот. С системой (3.2.1) можно проводить элементарные преобразования, подобные элементарным преобразованиям матриц (сложение уравнений, перестановку уравнений, умножение обеих частей уравнений на некоторое число), получая при этом системы эквивалентные системе (3.2.1).

Составим матрицу А=(а_ij)_mxn из коэффициентов системы (3.21)

а₁₁ а₁₂… а_1n
а₂₁ а₂₂… а_{2 n}
- - - - - - - - -

A = а_i1 a_i2 …. a_in

- - - - - - - - -

a_m1a_m2 …a_{mn mxn}

и введем столбцевые матицы из неизвестных и свободных членов

x₁ b₁

x₂ b₂

- -

Χ= -; B= -

- -

x _{n nx1 ­}b_{n nx1}

Найдем произведение матриц АХ

а₁₁ а₁₂… а_1n x₁ а₁₁ x₁+ а₁₂ x₂+…+ а_1n x_n

а₂₁ а₂₂… а_{2 n}x₂а₂₁ x₁+ а₂₂ x₂+…+ а_{2 n}x_n

- - - - - - - - - - - - - - - - - - - - - - - - - - -

АХ= а_i1 a_i2 … a_in - = - - - - - - - - - - - - - - - - -

- - - - - - - - - - - - - - - - - - - - - - - - - - -

a_m1 a_m2 …a_mn x_n a_m1 x₁+ a_m2x₂+…+ a_mnx_n

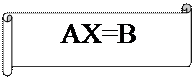Получена столбцевая матрица, элементы которой совпадают с левыми частями системы (3.2.1). Причем эти элементы равны соответствующим элементам матрицы В. А это означает, что матрицы АХ и В так же равны, т.е.

(3.2.2)

Получена матричная запись системы (3.2.1) или матричное уравнение.

Если ввести векторы

a_1j b₁

a­_2j b₂ A_j= - B= -

- -

a_mj b_m

то систему (3.2.1) можно записать в векторной форме

_n

A₁x₁+A₂x₂+…+A_nx_n =∑ A_j­x_j = B

_j=1