Задача Коши.
Рассмотрим уравнение.
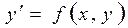 (13.6)
(13.6)

 Пусть функция
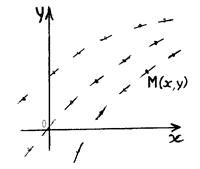
Пусть функция 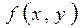 определена в области D плоскости xOy. Очевидно, уравнение (13.6) ставит всякой точке М (x, y) определенное значение производной y', то есть определяет в точке М (x, y) угловой коэффициент касательной
определена в области D плоскости xOy. Очевидно, уравнение (13.6) ставит всякой точке М (x, y) определенное значение производной y', то есть определяет в точке М (x, y) угловой коэффициент касательной 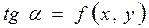 к интегральной кривой, проходящей через эту точку. Можно сказать, что уравнение (13.6) определяет совокупность направлений или поле направлений на плоскости xOy (рис.13.3).
к интегральной кривой, проходящей через эту точку. Можно сказать, что уравнение (13.6) определяет совокупность направлений или поле направлений на плоскости xOy (рис.13.3).
Таким образом, решение дифференциального уравнения (13.6), разрешенного относительно производной, сводится к отысканию кривых, направления касательных к которым в каждой точке плоскости совпадают с полем направлений.
Задача отыскания частного решения дифференциального уравнения 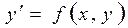 , разрешенного относительно производной, удовлетворяющего начальному условию
, разрешенного относительно производной, удовлетворяющего начальному условию 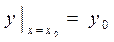 называется задачей Коши. Существование и единственность решения задачи Коши утверждается следующей теоремой:
называется задачей Коши. Существование и единственность решения задачи Коши утверждается следующей теоремой:
 Теорема. Пусть в дифференциальном уравнении
Теорема. Пусть в дифференциальном уравнении 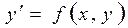 функция
функция 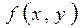 непрерывна и имеет непрерывную частную производную по y точке
непрерывна и имеет непрерывную частную производную по y точке 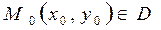 плоскости xOy. Тогда существует, причем единственное, решение
плоскости xOy. Тогда существует, причем единственное, решение 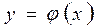 этого уравнения, такое, что
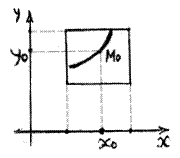
этого уравнения, такое, что 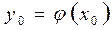 . Геометрически это означает, что через каждую точку
. Геометрически это означает, что через каждую точку 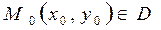 . проходит одна и только одна интегральная кривая (рис.13.4.).
. проходит одна и только одна интегральная кривая (рис.13.4.).
|
|
|

 2014-02-05
2014-02-05 416
416








