Определение. Характеристической функцией 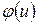 случайной величины
случайной величины 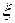 называется комплекснозначная функция, определенная при
называется комплекснозначная функция, определенная при 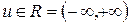 соотношением
соотношением
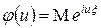 . (1)
. (1)
Пусть 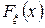 — функция распределения случайной величины, тогда формулу (15.1) можно записать в виде
— функция распределения случайной величины, тогда формулу (15.1) можно записать в виде
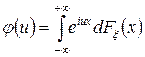 .
.
В случае существования плотности 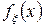 случайной величины
случайной величины 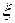 эту формулу можно переписать следующим образом
эту формулу можно переписать следующим образом
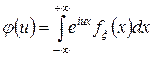 . (2)
. (2)
Непосредственно из определения вытекают свойства характеристической функции:
1) 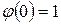 ,
, 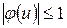 для всех действительных
для всех действительных 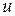 .
.
2) 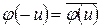 .
.
3) 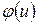 — равномерно непрерывная функция на всей числовой оси.
— равномерно непрерывная функция на всей числовой оси.
4) Характеристическая функция положительно определена, т.е. для любых действительных чисел 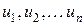 и любых комплексных чисел
и любых комплексных чисел 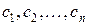
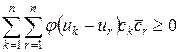 .
.
5) Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых.
Действительно, пусть 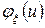 — характеристическая функция случайной величины
— характеристическая функция случайной величины 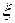 ,
, 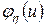 — случайной величины
— случайной величины 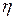 , тогда характеристическая функция их суммы
, тогда характеристическая функция их суммы 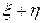 равна
равна
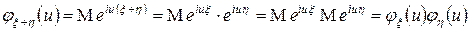 .
.
6) Если 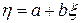 , где
, где 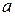 и
и 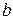 — некоторые постоянные, то
— некоторые постоянные, то 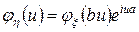 .
.
Не сложно видеть, что 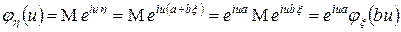 .
.
7) Характеристическая функция однозначно определяет распределение случайной величины.
Если случайная величина 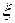 абсолютно непрерывна, выражение (2) есть преобразование Фурье функции
абсолютно непрерывна, выражение (2) есть преобразование Фурье функции 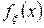 . Для абсолютно непрерывной величины
. Для абсолютно непрерывной величины 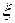 плотность
плотность 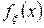 восстанавливается по ее характеристической функции
восстанавливается по ее характеристической функции 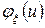 следующим образом:
следующим образом:
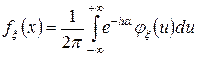 .
.
Зная характеристическую функцию дискретной целочисленной случайной величины 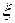 , такой что
, такой что 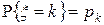 ,
, 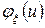 можно восстановить ее распределение. Не трудно видеть, что справедливы равенства:
можно восстановить ее распределение. Не трудно видеть, что справедливы равенства:
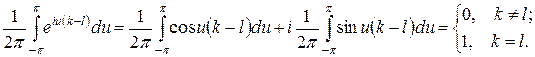
В силу того, что 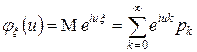 , имеем
, имеем
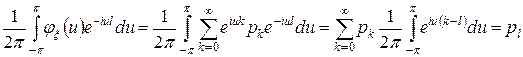 .
.
Таким образом, закон распределения восстановлен.
Еще одно важное свойство характеристических функций сформулируем в виде теоремы.
Теорема. Если существует абсолютный начальный момент порядка 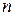
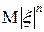 , то функция
, то функция 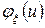 имеет
имеет 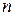 непрерывных производных и справедливо равенство
непрерывных производных и справедливо равенство
 .
.
При этом имеет место соотношение
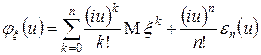 , (3)
, (3)
здесь 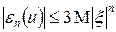 и
и 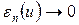 при
при 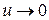 .
.
Доказательство. В силу того, что 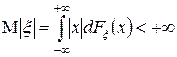 , интеграл
, интеграл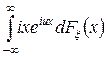 равномерно сходится по
равномерно сходится по 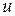 . Следовательно
. Следовательно
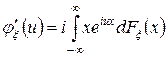 ,
, 
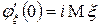 .
.
Далее, используя метод математической индукции, получим требуемое в теореме равенство
 .
.
Запишем разложение функции 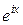 в ряд Тейлора в окрестности нуля с остаточным членом в форме Лагранжа
в ряд Тейлора в окрестности нуля с остаточным членом в форме Лагранжа
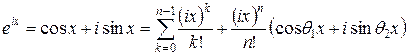 ,
,
здесь 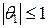 ,
, 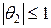 . Поэтому
. Поэтому
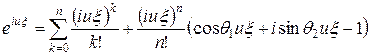 .
.
Таким образом,
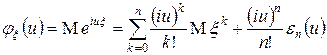 ,
,
где 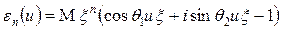 . Не трудно видеть, что
. Не трудно видеть, что 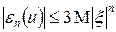 . Из теоремы Лебега о предельном переходе под знаком интеграла следует, что
. Из теоремы Лебега о предельном переходе под знаком интеграла следует, что 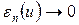 при
при 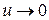 .
.
 2014-02-05
2014-02-05 746
746








