I.При известной дисперсии.
Рассмотрим оценку 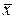 МО mx нормально распределенной СВ Х с известной дисперсией s2:
МО mx нормально распределенной СВ Х с известной дисперсией s2: 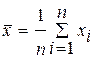 . Если СВ Х распределена по нормальному закону, то выборочное среднее
. Если СВ Х распределена по нормальному закону, то выборочное среднее 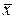 будет также распределено по нормальному закону с МО
будет также распределено по нормальному закону с МО 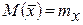 и дисперсией
и дисперсией 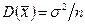 :
:
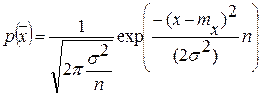 . Введем СВ
. Введем СВ 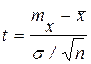 , которая имеет нормированное нормальное распределение с нулевым МО и единичной дисперсией. Тогда вероятность Р=1-a того, что СВ t (рис.18) не отклонится от своего МО на величину, больше чем ta/2 находится по формуле Р{-ta/2<u< ta/2}=Ф*(ta/2)- Ф*(-ta/2)= =1-a.
, которая имеет нормированное нормальное распределение с нулевым МО и единичной дисперсией. Тогда вероятность Р=1-a того, что СВ t (рис.18) не отклонится от своего МО на величину, больше чем ta/2 находится по формуле Р{-ta/2<u< ta/2}=Ф*(ta/2)- Ф*(-ta/2)= =1-a.
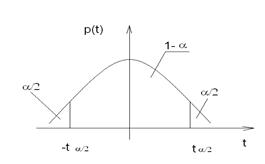
Рис.18
Принимая во внимание, что функция распределения Ф*(t) связана с функцией Лапласа Ф(t) соотношениями (рис.18): Ф(t)=0,5+ Ф*(t), Ф(t)=0,5- Ф*(t), получим
Р{-ta/2<u< ta/2}=2Ф(ta/2)=1-a. Поскольку функция Ф(t) непрерывна и возрастает на интервале [0,¥) от 0 до 0,5, то для любого числа a, удовлетворяющего неравенству 0<1-a<1, существует единственное число ta/2 такое, что Ф(ta/2)=1/2(1-a). Для заданной вероятности Р=1-a по таблице значений функции Лапласа Ф(t) можно найти соответствующее значение ta/2.
С надежностью Р=1-a можно утверждать, что доверительный интервал 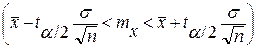 покрывает неизвестный параметр mx с точностью
покрывает неизвестный параметр mx с точностью 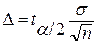
Т.о., доверительным интервалом называется такой интервал, относительно которого можно с заранее определенной, близкой к 1, вероятностью утверждать, что он содержит не известное нам истинное значение параметра mx:
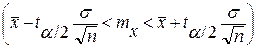 . Из этого соотношения видно что, чем точнее при данном значении s мы хотим оценить среднее значение, тем больше n экспериментов необходимо провести. С увеличением надежности (уменьшением a) доверительный интервал расширяется, т.е. точность уменьшается. Если задать точность D и вероятность a, то можно найти минимальный объем выборки n, который обеспечит заданную точность D:
. Из этого соотношения видно что, чем точнее при данном значении s мы хотим оценить среднее значение, тем больше n экспериментов необходимо провести. С увеличением надежности (уменьшением a) доверительный интервал расширяется, т.е. точность уменьшается. Если задать точность D и вероятность a, то можно найти минимальный объем выборки n, который обеспечит заданную точность D: 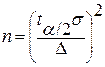 . Поскольку концы интервала представляют собой СВ, то их называют также доверительными границами. Если величина Х распределена не по нормальному закону распределения, то поскольку величина
. Поскольку концы интервала представляют собой СВ, то их называют также доверительными границами. Если величина Х распределена не по нормальному закону распределения, то поскольку величина 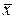 представляет собой сумму независимых, одинаково распределенных СВ, согласно предельной теореме при достаточно больших n (n³30) ее закон распределения близок к нормальному.
представляет собой сумму независимых, одинаково распределенных СВ, согласно предельной теореме при достаточно больших n (n³30) ее закон распределения близок к нормальному.
II.При неизвестной дисперсии:
Рассмотрим оценку 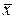 МО mx нормально распределенной СВ Х с неизвестной дисперсией s2:
МО mx нормально распределенной СВ Х с неизвестной дисперсией s2: 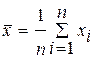 . Для оценивания дисперсии s2 используем оценку
. Для оценивания дисперсии s2 используем оценку 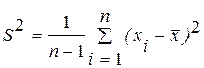 . Величина
. Величина 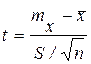 , при этих условиях имеет место t-распределение (распределение Стьюдента) с числом степеней свободы k=n-1. Для нахождения доверительного интервала значения mx задаемся надежностью Р=1-a по таблице t-распределения для уровня значимости a/2 (соответствующего односторонней критической области см. рис. 18), из условия P{½t½<ta/2}=1-a определяем значение ta/2 и строим доверительный интервал:
, при этих условиях имеет место t-распределение (распределение Стьюдента) с числом степеней свободы k=n-1. Для нахождения доверительного интервала значения mx задаемся надежностью Р=1-a по таблице t-распределения для уровня значимости a/2 (соответствующего односторонней критической области см. рис. 18), из условия P{½t½<ta/2}=1-a определяем значение ta/2 и строим доверительный интервал:
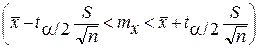 .
.
 2014-02-02
2014-02-02 1159
1159
