Другие числовые характеристики

Определение 12. Начальным моментом порядка 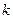случайной величины Х называется математическое ожидание величины : .

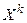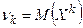Замечание 1. Для непрерывной случайной величины 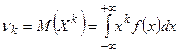, при условии, что интеграл сходится абсолютно.

Замечание 2. В частности, , .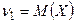

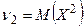Определение 13. Центральным моментом порядка 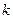случайной величины Х называется математическое ожидание величины : .

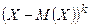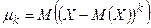Замечание. Для непрерывной случайной величины 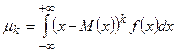, при условии, что интеграл сходится абсолютно.

Определение 14. Абсолютным центральным моментом порядка 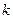случайной величины Х называется математическое ожидание величины : .

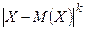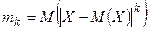Замечание. Всякое распределение вероятностей называют теоретическим распределением. При изучении различных теоретических распределений, отличных от нормального, возникает необходимость оценить это различие. С этой целью вводят специальные характеристики: асимметрию и эксцесс.

Определение 15. Распределение называется симметричным, если график его плотности вероятности симметричен относительно прямой .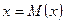

Замечание. Равномерное и нормальное распределение симметричны.

Лемма. Для симметричного распределения каждый центральный момент нечётного порядка равен нулю.

Замечание. Для несимметричных распределений центральные моменты нечётных порядков, кроме первого, отличны от нуля. Следовательно, они могут служить характеристиками несимметричности распределения.

Определение 15. Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратичного отклонения: .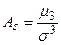

Замечание. Для нормального распределения 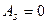. 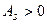, если «длинная часть» кривой распределения расположена справа от прямой 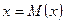, , 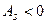если слева. Практически определяют знак асимметрии по расположению кривой распределения относительно моды плотности распределения: если длинная часть кривой расположена правее моды, то 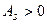, если слева – .

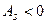Замечание. Для оценки «крутизны» (большего или меньшего подъёма кривой теоретического распределения по сравнению с нормальным) пользуются эксцессом.

Определение 16. Эксцессом теоретического распределения называется величина .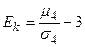

Замечание. Для нормального распределения 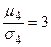, следовательно, 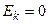. Если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой: если 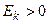, то кривая имеет более высокую и острую вершину, чем нормальная кривая; если 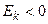, то кривая имеет более низкую и плоскую вершину, чем нормальная кривая. При этом предполагается, что нормальное и теоретическое распределение имеют одинаковые математические ожидания и дисперсии.

§ 15. Одинаково распределённые взаимно независимые случайные величины

Замечание. По закону распределения можно найти числовые характеристики случайной величины. Отсюда следует, что если несколько случайных величин имеют одинаковые распределения, то их числовые характеристики одинаковы.

Рассмотрим п взаимно независимых случайных величин , , 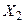…, , 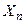которые имеют одинаковые распределения, а следовательно, и одинаковые характеристики (математическое ожидание, дисперсию и др.). Пусть , , .

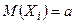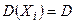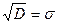Обозначим среднее арифметическое рассматриваемых случайных величин случайную величину 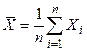. Следующие теоремы устанавливают связь между числовыми характеристиками среднего арифметического 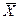и соответствующими характеристиками каждой отдельной величины.

Теорема 1. Математическое ожидание среднего арифметического 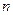одинаково распределённых взаимно независимых случайных величин равно математическому ожиданию 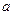каждой из величин: .

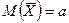Доказательство. .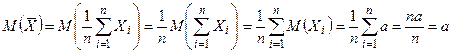

Теорема 2. Дисперсия среднего арифметического 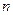одинаково распределённых взаимно независимых случайных величин в 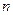раз меньше дисперсии 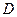каждой из величин: .

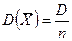Доказательство. .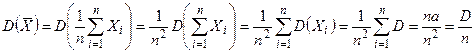

Теорема 3. Среднее квадратическое отклонение среднего арифметического 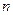одинаково распределённых взаимно независимых случайных величин в 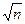раз меньше среднего квадратического отклонения 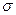каждой из величин: .

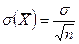Доказательство. .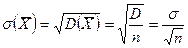

Вывод. Так как дисперсия и СКО служат мерами рассеяния случайной величины, то среднее арифметическое достаточно большого числа взаимно независимых случайных величин имеет значительно меньшее рассеяние, чем каждая отдельная величина. Следовательно,

1) среднее арифметическое даёт результат более надёжный, чем отдельные измерения;

2) с увеличением числа измерений надёжность этого результата возрастает.