Некоторые теоремы о дифференцируемых функциях

ПРОИЗВОДНЫХ

ИССЛЕДОВАНИЕ ФУНКЦИЙ ПРИ ПОМОЩИ

Теорема (Ролля). Если функция f (x) непрерывна на отрезке [ a; b ], дифференцируема на интервале (а; b) и на концах отрезка принимает одинаковые значения f (а) = f (b), то найдется хотя бы одна точка с 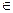(а; b), в которой производная f '(x) обращается в нуль, т. е. f '(с) = 0.

Геометрически теорема Ролля означает, что на графике функции у = f (x) найдется точка, в которой касательная к графику параллельна оси Ох (см. рис. 1 и 2). На рисунке 3 таких точек две.

Теорема (Коши). Если функции f (x) и φ (х) непрерывны на отрезке [ a; b ], дифференцируемы на интервале (а; b), причем φ ′(х) ≠ 0 для х 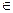(а; b), то найдется хотя бы одна точка c 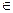(а; b) такая, что выполняется равенство

.

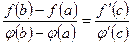Теорема (Лагранжа). Если функция f (x) непрерывна на отрезке

[ a; b ], дифференцируема на интервале (а; b), то найдется хотя бы одна точка с 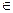(а; b) такая, что выполняется равенство

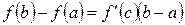(11.2)

Следовательно, геометрический смысл теоремы Лагранжа таков: на графике функции у = f (x)найдется точка C (с; f (с)) (см. рис. 4), в которой касательная к графику функции параллельна секущей АВ.

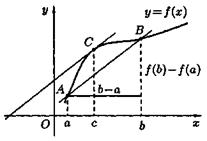
Рис. 4.

Следствие. Если производная функции равна нулю на некотором промежут­ке, то функция постоянна на этом промежутке.

Следствие. Если две функции имеют равные производные на некотором про­межутке, то они отличаются друг от друга на постоянное слагаемое.