Нуль-полюсные диаграммы

Из теории линейных аналоговых фильтров и теории функций комплексного переменного известно, что частотные характеристики фильтра можно определить, используя нуль-полюсное представление его комплексной передаточной функции.

В качестве примера рассмотрим аналоговую передаточную функцию 2-го порядка с действительными полюсами  s _П1 и s _П2:

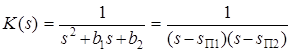          .                           (3.21)

Для получения АЧХ фильтра надо заменить s на j w и найти модуль получившегося выражения:

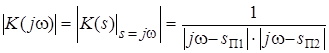          .                         (3.22)

Абсолютное значение каждого множителя в (3.22)  можно интерпретировать как длину соответствующего вектора в плоскости комплексной переменной s с координатами s, j w (рис. 3.4). Векторы (j w – s _П1) и (j w – s _П2) – это векторы, соединяющие концы векторов s _П1 и s _П2 с концом вектора j w. Векторы s _П1 и s _П2 проводятся из начала координат до места расположения соответствующего полюса. Вектор j w  проводится вдоль оси ординат до точки с координатой, равной значению текущей частоты w.  Значение АЧХ на этой частоте можно найти, если определить графически длину векторов (j w – s _П1) и (j w – s _П2), а затем взять обратное значение произведения длин этих векторов.

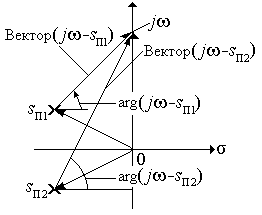
Рис. 3.4.

Определение АЧХ и ФЧХ аналогового фильтра по нуль-полюсной диаграмме.

 

Фазочастотная характеристика определяется в соответствии с выражением:

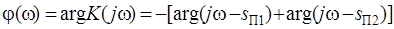      .         (3.23)

В общем случае нуль-полюсное представление передаточной функции фильтра произвольного вида выглядит следующим образом:

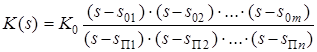            ,                    (3.24)  

где s ₀₁,..., s _{0 m} – координаты нулей (корней числителя), s _П1,..., s _{П n} – координаты полюсов.

В этом случае для определения значения АЧХ на частоте w надо найти произведение длин векторов 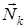, соединяющих каждый из нулей с точкой j w на оси ординат, и произведение длин векторов 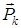, соединяющих каждый из полюсов с точкой j w,  поделить первое произведение на второе, а также учесть постоянный множитель K ₀:

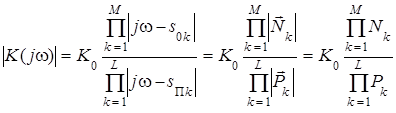,            (3.25)

где N_k и P_k - модули (длины) векторов.

Фазочастотная характеристика определяется следующим образом. Вычисляется сумма аргументов векторов 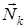 и сумма аргументов векторов  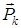для выбранной частоты w, затем определяется разность между этими суммами. Эта разность и представляет собой значение фазы на частоте w. Выражение для ФЧХ имеет вид:

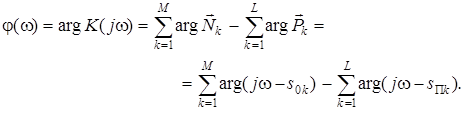     (3.26)       

Для иллюстрации описанного способа определения АЧХ рассмотрим простой пример, когда передаточная функция фильтра описывается выражением

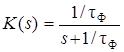                             .                                            (3.27)

Функция K (s)рассматриваемого примера имеет один нуль (корень числителя) s ₀ с координатами s = - ∞,   j w = 0 и один полюс (корень знаменателя) s _П с координатами s = -1/t_F,   j w = 0.

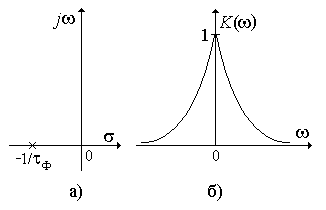
Рис. 3.5.

Определение АЧХ аналогового фильтра по нуль-полюсной диаграмме: а)нуль-полюсная диаграмма, б) АЧХ фильтра.

 

На рис. 3.5,апоказано расположение полюса в s -плоско­сти. Поскольку нуль удален на оси s  в бесконечность, то он не влияет на избирательные свойства фильтра. Значения АЧХ находятся в соответствии с выражением (3.25), которое в рассматриваемом случае записывается в виде:

              .

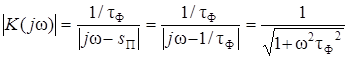Форма АЧХ фильтра определяется степенью приближения к полюсу точки, движущейся по оси j w. Наименьшее расстояние этой точки до полюса будет в том случае, когда w = 0, следовательно, на нулевой частоте АЧХ имеет максимальное значение. При увеличении абсолютного значения w расстояние от движущейся вдоль оси точки до полюса увеличивается, а значение АЧХ уменьшается. Примерная форма АЧХ рассмат­риваемого фильтра для положительных и отрицательных частот показана на рис 3.5,б.

Аналогичный способ оценки частотных характеристик по нуль-полюсной диаграмме используется и для цифровых фильтров. Прежде чем описывать этот способ, рассмотрим, как осуществляется переход от комплексной плоскости   s к комплексной плоскости   z.

Выше была отмечена связь между z и s:

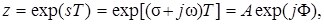                                    (3.28)

где 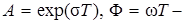круговая цифровая частота.

Комплексная величина z, представленная в экспонен­циальной форме (3.28), описывается в z -плоскости вектором, имеющим длину А и угол Ф относительно ве­щественной оси х (рис. 3.6). При возрастании переменной Ф конец вектора движется по окружности с радиусом А про­тив часовой стрелки.

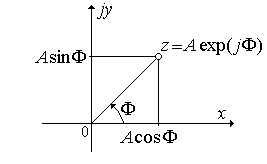
Рис. 3.6.

Графическое представление комплексной величины z.

 

Соотношение (3.28) и рисунки 3.5,а и 3.6 позволяют предста­вить закономерности преобразования s -плоскости в z -плоскость. Очевидно, что движение в s -плоскости вверх по оси частот j w(w= var, s= 0) переходит в z -плоскости в цикли­ческое вращение по окружности единично­го радиуса (Ф = var, A = 1) против часовой стрелки. При этом первый полный оборот по окружности в z -плоскости, когда Ф меняется в пределах от нуля до 2p, соответствует из­менению частоты в s -плоскости в пределах w= 0…2p/ T.

Продолжая эти рассуждения, можно установить, что лю­бая вертикальная прямая в левой s -полуплоскости (w= var, s<0) отображается в z -плоскости окружностью с радиусом А = exp(s T)<1 (рис. 3.7). При этом вертикальная прямая в s- плоскости, бесконечно удаленная влево по оси s, стягивается в z -плоскости в точку, совпадающую с началом координат. Таким образом, вся левая s -полуплоскость отображается в z -плоскости в круге с радиусом, рав­ным 1.

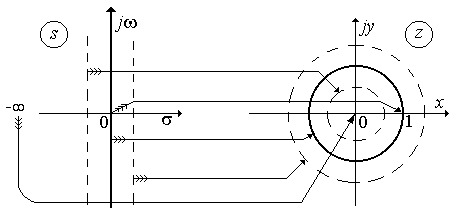
Рис. 3.7.

Отображение s -плоскости в z -плоскость.

 

Очевидно, что правая s -полуплоскость (s>0) отобра­жается в z -плоскости бесконечной областью, лежащей вне круга единичного радиуса (рис. 3.7).

Нуль-по­люсной диаграммой цифрового фильтра называется график, на котором нули и полюсы передаточной функции фильтра изображены в z -плоскости относи­тельно окружности единичного радиуса.

Для оценки АЧХ цифрового фильтра с помощью нуль-полюсной диаграммы преобразуем вначале общее выражение передаточной функции (3.17), используя известное поло­жение: «каждый многочлен f (x) степени N относительно x может быть единственным способом представлен в виде произведения постоянной и линейных множителей вида (x - x_k)»­:

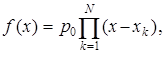                                                                      (3.29)

где x_k - корни многочлена f (x), в числе которых комплексные корни могут быть только в виде сопряженных пар; p ₀ - постоянная величина.

Первый шаг преобразования (3.17) состоит в изменении знака показателей переменной z:

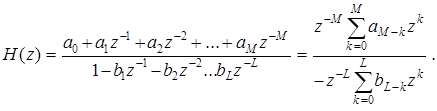      (3.30)

При выводе выражения (3.30) было принято: - b ₀ = 1.

Используя (3.29), представим (3.30) в виде:

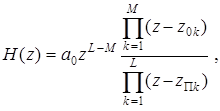                                                     (3.31)

где z _{0 k} - M нулей, а z _{П k} - L полюсов функции H (z).

При определении АЧХ цифрового фильтра считают, что на его входе действует незатухающая синусоида. В этом случае, в соответствии с выражением (3.28), следует полагать, что s = 0, A = 1, а z = exp(j F). Подставляя это выражение для z в (3.31), для комплексного коэффициента передачи получим формулу:

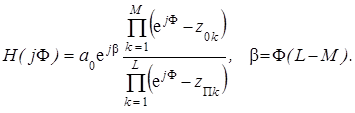                           (3.32)

Учитывая, что 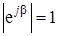, определим АЧХ цифрового фильтра как модуль H (j F):

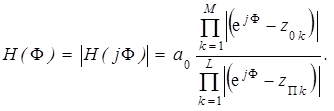                              (3.33)

Выражение (3.33) подобно выражению (3.25), полученному для определения АЧХ аналогового фильтра, но здесь обычная для аналоговых фильтров частота w заменена на цифровую F = w T. Подобны и геометрические интерпретации этих выражений.

В каждом сомножителе числителя в (3.33) составляющие exp(j F) и z _{0 k} могут быть представлены в z -плоскости векторами. Тогда векторные разности

                    

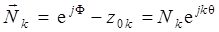
также представляют собой векторы длиной N_k, как это показано на рис. 3.8,а для случая двух комплексно-сопряженных нулей.

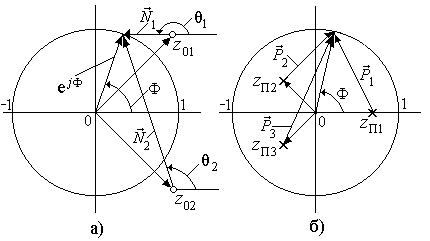
Рис. 3.8.

Нуль-полюсные диаграммы цифровых фильтров а)для случая нулей, б)для случая полюсов.

 

Таким образом, числитель в (3.33) может быть представ­лен следующим образом:

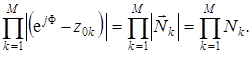                                           (3.34)

Аналогична запись и для знаменателя в (3.33):

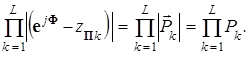                                                  (3.35)

где P_k - длины векторов k- тых разностей в знаменателе (3.33).

 

Для иллюстрации на рис. 3.8,бпоказано построение этих векто­ров для случая одного вещественного z _П1  и двух комплексно-сопряженных z _П2, z _П3 полюсов.

В соответствии с формулами (3.34) и (3.35), выражение (3.33) для АЧХ можно переписать в виде:

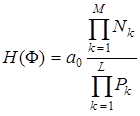                        .                                 (3.36)

Описанный способ определения АЧХ удобен тем, что для оценки АЧХ достаточно располагать записью передаточной функции цифрового фильтра в форме (3.31), которая обычно составляется на первых этапах проектирования.

Построение АЧХ в функции от цифровой частоты с помощью нуль-полюсных диаграмм следует начинать со значения Ф = 0 (точка 0,+1), двигаясь далее против часовой стрелки по окружности единичного ра­диуса в пределах удвоенного интервала Найквиста, т.е. в пределах изменения Ф от 0 до 2p. Дальнейшее движение по окружности приведет лишь к повторению копий АЧХ.

Нули и полюсы, расположенные в начале координат (z = 0), удалены от любой точки на окружности единичного радиуса на одинаковое расстояние r = 1.Следовательно, та­кие нули и полюсы не влияют на форму АЧХ.

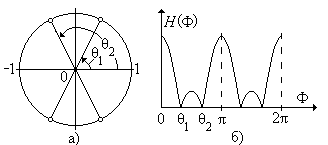
Рис. 3.9.

Связь АЧХ с расположением нулей: а) нуль-полюсная диаграмма; б) АЧХ.

 

Чем ближе расположен нуль к окружности единичного радиуса, тем меньше коэффициент передачи цифрового фильтра на соответствующей частоте. Если ряд нулей рас­положен непосредственно на окружности единичного радиуса, то на частотах, соответствующих месту расположения нулей, коэффициент передачи цифрового фильтра равен нулю (рис. 3.9). Отметим, что нуль-полюсная диаграмма на рис. 3.9 включает в себя еще и два полюса, расположенные в начале координат. При таком расположении полюсов они не влияют на АЧХ, а поэтому и не изображены, чтобы не загромождать рис. 3.9. Приближение полюса к окружности единичного радиуса вызывает увеличение коэффициента передачи циф­рового фильтра на соответствующей частоте, как это показано на рис. 3.10, где изображены еще и два нуля в начале координат нуль-полюсной диаграммы.

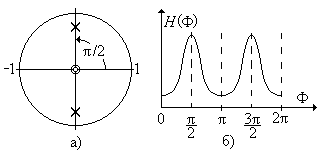
Рис. 3.10.

Связь АЧХ с расположением полюсов: а) нуль-полюсная диаграмма; б) АЧХ.

 

Известно, что полюсы передаточной функции устойчивого аналогового фильтра расположены в левой s -полуплоскости (s<0). Поскольку при z -преобразовании левая s -полуплоскость переходит внутрь круга единичного радиуса, то условие устойчивости цифрового фильтра формулируется так: цифровой фильтр устойчив, если полюсы его передаточной функции расположены внутри окружности единичного радиуса. Особые точки – нули передаточной функции могут располагаться в любом месте плоскости комплексной переменной z, так как они не влияют на устойчивость фильтра.

Помимо ориентировочной оценки формы АЧХ, нуль-полюсные диаграммы ЦФ позволяют в ряде случаев сравнительно просто вывести и аналитические выражения для АЧХ.

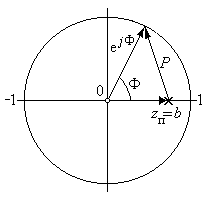
Рис. 3.11.

К  расчету АЧХ цифрового фильтра.

 

В качестве первого примера рассчитаем АЧХ низкочастотного ЦФ 1-го порядка, рассмотренного в параграфе 3.2. Передаточная функция фильтра описывается выражением (3.15) и имеет один нуль z ₀ = 0 и один полюс z _П= b. Нуль-полюсная диаграмма фильтра изображена на рис. 3.11. В соответствии с нуль-полюсной диаграммой и выражением (3.36) АЧХ рассматриваемого фильтра находится по формуле:

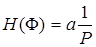                              .                               (3.37)

Для определения P используем известную формулу из курса геометрии, которая связывает длину стороны C с длинами сторон A, B и косинусом угла F между сторонами A и  B:

                         C ² = A ² + B ² – 2 AB cosF.

Согласно этой формуле и рис. 3.11:

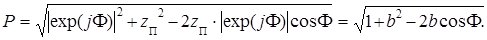
Подставив P в (3.37) получим следующее выражение для АЧХ:

                        

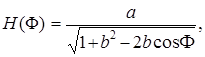
которое совпадает с выражением, выведенным ранее в подразделе 2.4.

Другой пример относится к ЦФ 2-го порядка с комплексно-сопряженными нулями и полюсами (рис. 3.12). АЧХ такого ЦФ имеет примечательную особенность – наличие интенсивного и, что главное, узкополосного "всплеска" на частоте F₀. Полосу пропускания этого "всплеска" в принципе можно сделать сколь угодно малой за счет приближения полюсов и нулей к окружности единичного радиуса. Правда, это потребует увеличения разрядности вычислителя.

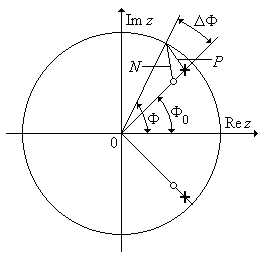
Рис. 3.12.

Нуль-полюсная диаграмма селективного фильтра.

 

Рассчитаем АЧХ рассматриваемого ЦФ. Для упрощения расчета учтем ряд обстоятельств. Во-первых, заметное различие в расстояниях P (до полюса) и N (до нуля) имеет место только в небольшой области частот вблизи значения F₀. В удаленных от частоты F₀ областях расстояния P  и N практически одинаковы, и, следовательно, коэффициент передачи ЦФ, равный отношению P / N, в этих областях близок к единице и практически  не  меняется. Таким  образом,  при  расчете  АЧХ достаточно  учитывать  только  расстояния  до нуля  и  полюса,  расположенных  в области вблизи F₀.  При изменении текущей частоты  вектор exp(j F) отклоняется  в этой области на угол F = F₀ ± DF  (рис. 3.12).    Во-вторых, так как резкое изменение АЧХ происходит в небольшом интервале частот F = F₀ ± DF, то соответствующая этому интервалу дуга окружности единичного радиуса может быть аппроксимирована прямой. Длина этой дуги равна DF× R, где R - радиус единичной окружности. Учитывая перечисленные обстоятельства, расчет АЧХ будем проводить с использованием геометрических построений, приведенных на рис. 3.13, где в увеличенном виде показана часть рис. 3.12. В соответствии с выражением (3.36) и рис. 3.13 АЧХ определяется формулой:

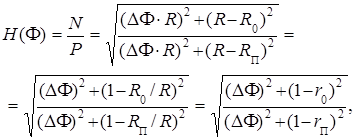                      (3.38)

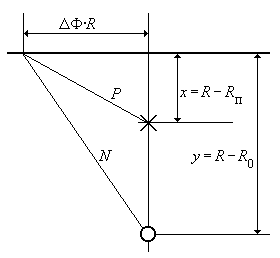
Рис. 3.13.

К  расчету АЧХ селективного фильтра.

 

где R ₀ и R _П - расстояния от центра окружности до, соответственно, нуля и полюса; r ₀ и r _П - их значения, нормированные к радиусу окружности; DF = Dw T = 2pD f / f _Д.

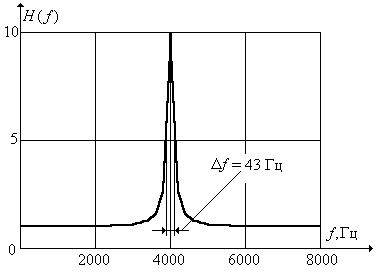
Рис. 3.14.

АЧХ селективного фильтра.

 

На рис. 3.14 приведен график АЧХ, рассчитанный по (3.38) при следующих значениях параметров: r _П = 0,995; r ₀ = 0,95; f _Д = 16 кГц. График построен для отклонений D f от центральной частоты f ₀. Отметим, что само значение f ₀ не входит в выражение (3.38) для АЧХ, а только определяет положение "всплеска" на оси частот, не влияя на форму АЧХ. ЦФ рассмотренного типа может быть использован, например, для селекции пилот-сигнала, содержащегося в спектре обрабатываемого колебания.

В некоторых случаях при проектировании ЦФ может оказаться, что полюс выходит за пределы окружности единичного радиуса. При этом заданная АЧХ сохраняется, но ЦФ становится неустойчивым. Существует простой способ введения полюсов внутрь окружности единичного радиуса без изменения АЧХ.

Рассмотрим случай, когда неустойчивый ЦФ является результатом преобразования неустойчивого аналога-прототипа. В нуль-полюсной диаграмме неустойчивого аналога-прототипа полюсы расположены в правой полуплоскости, как показано на рис. 3.15,а, где с целью упрощения рисунка показан только один из пары комплексно-сопряженных полюсов с положительной действительной частью, он помечен звездочкой: s ^*_П.1 = +s_П + j w_П.

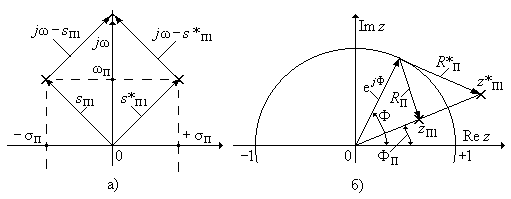
Рис. 3.15.

Преобразования нуль-полюсных диаграмм неустойчивых фильтров а)аналога-прототипа, б) цифрового.

 

Для того чтобы сделать аналог-прототип устойчивым при сохранении его АЧХ, необходимо переместить полюс s ^*_П.1 в левую полуплоскость, симметрично относительно оси j w, как это показано на рис. 3.15,а. Очевидно, что АЧХ аналога-прототипа не меняется при замене полюса с положительной действительной частью s ^*_П.1 на полюс с отрицательной действительной частью s _П.1, так как расстояния от точки с текущей частотой w до каждого из указанных полюсов одинаковы.

Полюсам неустойчивого аналога-прототипа соответствуют полюсы неустойчивого ЦФ (см. рис. 3.15,б, где показан только один из сопряженных полюсов, расположенный вне окружности единичного радиуса):

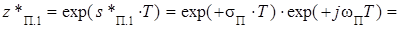
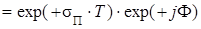                                                  .        (3.39)

Перемещению аналогового полюса s ^*_П.1 в левую полуплоскость на место полюса s _П.1 соответствует перемещение полюса z *_П.1 внутрь окружности единичного радиуса на место полюса z _П.1, выражение для которого имеет вид:

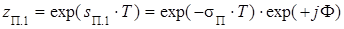           .                 (3.40)

В результате такого перемещения фильтр становится устойчивым. Покажем, что АЧХ фильтра при этом не меняется.      

При определении АЧХ фильтра с полюсом z _П.1 надо найти длину вектора 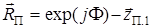, так как АЧХ обратно пропорциональна этой длине: H (w)~1/| 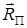|. Аналогичная связь устанавливается между АЧХ фильтра с полюсом z *_П.1 и длиной вектора 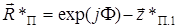: H *(w) ~ 1/| 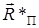|. Найдем длины указанных векторов.

,

.

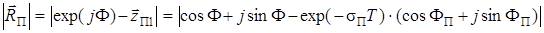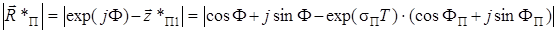После выполнения ряда преобразований получим:

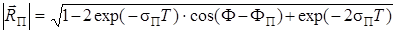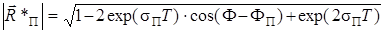      ,                                       =                 (3.41)

      = exp(s_П T) =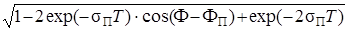

            = exp(s_П T) .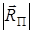

Отношение АЧХ обратно пропорционально отношению длин векторов, т.е. пропорционально отношению :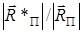

                 H (w)/ H *(w) ~ 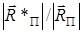 = exp(s_П T).                           (3.42)

Поскольку величина exp(s_П T) не зависит от частоты, то на основании (3.42) можно сделать вывод, что при перемещении неустойчивого полюса внутрь единичной окружности АЧХ фильтра повторяет прежнюю АЧХ с точностью до масштабного множителя.