no1. Правило Лопиталя.
Ниже будут приведены теоремы, с помощью которых удобно находить пределы вида 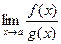 , где функции
, где функции  и
и 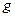 одновременно стремятся к нулю или к бесконечности при
одновременно стремятся к нулю или к бесконечности при 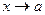 . Рецепт отыскания этих пределов, который содержится в этих теоремах, носит название правила Лопиталя.
. Рецепт отыскания этих пределов, который содержится в этих теоремах, носит название правила Лопиталя.
Теорема 1. Пусть функции  и
и 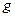 дифференцируемы на конечном или бесконечном интервале
дифференцируемы на конечном или бесконечном интервале  ,
,
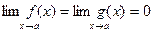
| (1) |
и 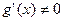 на
на  .
.
Тогда если существует конечный или бесконечный предел
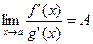
| (2) |
то существует и предел 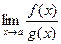 , причем
, причем
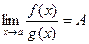
| (3) |
Д о к а з а т е л ь с т в о. Ограничимся доказательством для случая, когда интервал  конечен. Доопределим функции
конечен. Доопределим функции  и
и 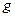 в точке
в точке 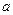 , положив
, положив
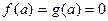
А тогда, каково бы ни было 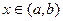 , в силу дифференцируемости этих функций на интервале
, в силу дифференцируемости этих функций на интервале  они будут непрерывными на отрезке
они будут непрерывными на отрезке 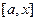 . Следовательно, на всяком таком отрезке
. Следовательно, на всяком таком отрезке 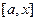
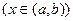 функции
функции  и
и 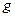 удовлетворяют условиям теоремы Коши о среднем значении. Поэтому на любом таком отрезке
удовлетворяют условиям теоремы Коши о среднем значении. Поэтому на любом таком отрезке 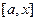 существует такая точка
существует такая точка 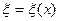
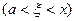 , что
, что
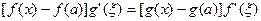
| (4) |
Заметим, что здесь по условию теоремы 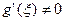 . Кроме того, в силу теоремы Ролля
. Кроме того, в силу теоремы Ролля 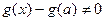 . Действительно, в противном случае, по этой теореме, нашлась бы такая точка
. Действительно, в противном случае, по этой теореме, нашлась бы такая точка 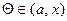 , что
, что 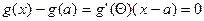 , а так как
, а так как 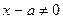 , (поскольку
, (поскольку 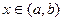 ), то это означает, что
), то это означает, что 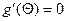 . Но это противоречит условию теоремы о том, что
. Но это противоречит условию теоремы о том, что 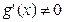 на
на 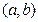 .
.
Из сделанных выше замечаний следует, что равенство (4) можно переписать в виде
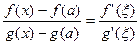 .
.
Но, так как 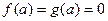 , то это равенство равносильно равенству
, то это равенство равносильно равенству
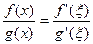 .
.
Учитывая теперь (2) и то, что 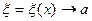 при
при 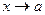 , в силу последнего равенства и теоремы о пределе суперпозиции, будем иметь
, в силу последнего равенства и теоремы о пределе суперпозиции, будем иметь
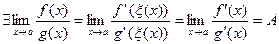 □
□
Замечание 1. Утверждение теоремы сохраняет свою силу если условие 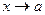 заменить на условие
заменить на условие 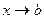 .
.
Теорема 2. Пусть функции  и
и 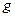 дифференцируемы на конечном или бесконечном интервале
дифференцируемы на конечном или бесконечном интервале  ,
,
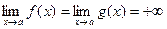
и 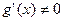 на
на  .
.
Тогда если существует конечный или бесконечный предел
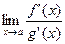
то существует и равный ему предел
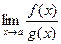 .
.
no2. Условия монотонности функции.
Теорема 1. Пусть функция  дифференцируема на интервале
дифференцируема на интервале 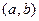 . Тогда имеют место следующие импликации:
. Тогда имеют место следующие импликации:
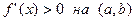 ⇒
⇒ 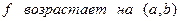 ⇒
⇒ 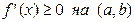 , (1)
, (1)
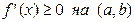 ⇒
⇒ 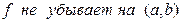 ⇒
⇒ 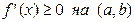 , (2)
, (2)
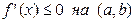 ⇒
⇒ 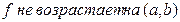 ⇒
⇒ 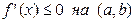 , (3)
, (3)
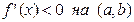 ⇒
⇒ 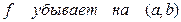 ⇒
⇒ 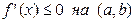 . (4)
. (4)
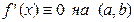 ⇒
⇒ 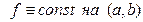 ⇒
⇒ 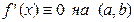 , (5)
, (5)
Д о к а з а т е л ь с т в о. Прежде всего заметим, что (5) следует из (2) и (3). Следовательно нужно доказать лишь (1)-(4).
Левые импликации в (1)-(5) доказываются на основе формулы конечных приращений Лагранжа. Выберем произвольные точки 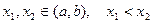 . По теореме Лагранжа найдется такая точка
. По теореме Лагранжа найдется такая точка 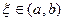 , что
, что
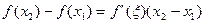
Отсюда, в частности, следует, что если 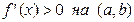 , то
, то 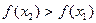 . В силу произвольности выбранных точек
. В силу произвольности выбранных точек 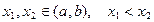 , это означает, что функция
, это означает, что функция  возрастает на
возрастает на 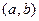 . Таким образом, доказана левая из импликаций (1). Аналогично доказываются левые импликации в (2)-(4).
. Таким образом, доказана левая из импликаций (1). Аналогично доказываются левые импликации в (2)-(4).
Правые импликации в (1)-(4) доказываются на основе определения производной. Пусть, например, функция 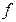 возрастает на
возрастает на 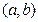 . Тогда для любого
. Тогда для любого 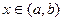 и любого
и любого 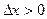 такого, что
такого, что 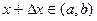 имеем
имеем
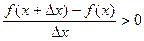 .
.
Переходя здесь к правостороннему пределу в точке 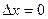 , по теореме о предельном переходе в неравенстве получим
, по теореме о предельном переходе в неравенстве получим
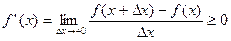 .
.
Так как выше точка 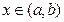 была выбрана произвольно, то это означает, что имеет место правая из импликаций (1). Аналогично доказываются правые импликации в (2)-(4) □
была выбрана произвольно, то это означает, что имеет место правая из импликаций (1). Аналогично доказываются правые импликации в (2)-(4) □
Замечание 1. Импликации (2), (3) и (5) для дифференцируемой на интервале 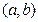 функции
функции 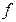 имеют смысл необходимых и достаточных условий и могут быть записаны в виде:
имеют смысл необходимых и достаточных условий и могут быть записаны в виде:
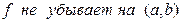 ⇔ ⇔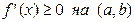
| (2’) |
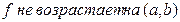 ⇔ ⇔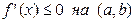
| (3’) |
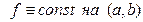 ⇔ ⇔ 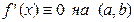
| (5’) |
Вместе с тем отметим, что левые из импликаций (1) и (4) не обратимы, что иллюстрирует приводимый ниже пример.
Пример 1. Функция 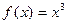 , очевидно, является возрастающей на всей вещественной оси, т.е. на интервале
, очевидно, является возрастающей на всей вещественной оси, т.е. на интервале 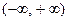 , но
, но 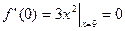 . Таким образом, условие
. Таким образом, условие 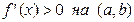 является достаточным, но не необходимым условием того, чтобы функция была возрастающей на интервале
является достаточным, но не необходимым условием того, чтобы функция была возрастающей на интервале 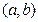 . Аналогично, если рассмотреть функцию
. Аналогично, если рассмотреть функцию 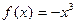 , то легко убедиться, в том, что условие
, то легко убедиться, в том, что условие 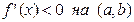 является достаточным, но не необходимым условием того, чтобы функция была убывающей на интервале
является достаточным, но не необходимым условием того, чтобы функция была убывающей на интервале 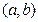 .
.
no3. Условия экстремума функции.
Необходимое условие локального экстремума доставляет теорема Ферма. Очевидно, она допускает следующее усиление.
Теорема 2. Если функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  и имеет в ней локальный экстремум, то либо функция
и имеет в ней локальный экстремум, то либо функция 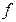 не дифференцируема в точке
не дифференцируема в точке  , либо
, либо
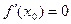
| (1) |
Определение 1. Если дифференцируемая в точке  функция удовлетворяет условию (1), то эта точка называется стационарной точкой функции
функция удовлетворяет условию (1), то эта точка называется стационарной точкой функции  .
.
Следующая очевидная теорема доставляет достаточное условие локального экстремума функции, а также достаточные условия отсутствия этого экстремума.
Теорема 3. Пусть функция  определена в некоторой окрестности
определена в некоторой окрестности 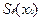 точки
точки  , непрерывна в самой точке
, непрерывна в самой точке  и дифференцируема в проколотой окрестности
и дифференцируема в проколотой окрестности 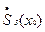 этой точки. Тогда если при “переходе” через точку
этой точки. Тогда если при “переходе” через точку  “слева на право” производная
“слева на право” производная 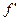 меняет знак с плюса на минус, то в точке
меняет знак с плюса на минус, то в точке  функция
функция  имеет локальный максимум. Если же при таком переходе через точку
имеет локальный максимум. Если же при таком переходе через точку  производная
производная 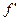 меняет знак с минуса на плюс, то в точке
меняет знак с минуса на плюс, то в точке  она имеет локальный минимум. Наконец, если при переходе через точку
она имеет локальный минимум. Наконец, если при переходе через точку  производная не меняет своего знака, то в этой точке нет локального экстремума.
производная не меняет своего знака, то в этой точке нет локального экстремума.
Теорема 4 (достаточное условие локального экстремума в терминах высших производных). Пусть функция 
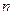 раз дифференциркема в точке
раз дифференциркема в точке  (
(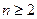 ). Тогда если
). Тогда если
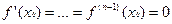 (2) и
(2) и 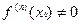 , то при
, то при 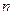 нечетном в точке
нечетном в точке  нет локального экстремума, а при
нет локального экстремума, а при 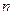 четном есть, при этом в последнем случае (т.е. при
четном есть, при этом в последнем случае (т.е. при 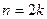 ,
, 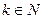 ) если
) если 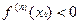 , то в этой точке она имеет локальный максимум, а если
, то в этой точке она имеет локальный максимум, а если 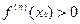 , то в она имеет в ней локальный минимум.
, то в она имеет в ней локальный минимум.
Д о к а з а т е л ь с т в о. В силу условия (2) локальная формула Тейлора функции  в точке
в точке  имеет вид
имеет вид
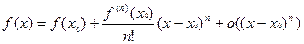 ,
,
а поскольку 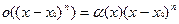 , где
, где 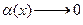 при
при  , то ее можно переписать в виде
, то ее можно переписать в виде
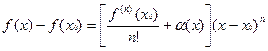 . .
| (3) |
Так как 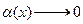 при
при  и
и 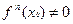 , то в достаточно малой окрестности точки
, то в достаточно малой окрестности точки  знак выражения, стоящего в квадратных скобках в формуле (3), будет совпадать со знаком производной
знак выражения, стоящего в квадратных скобках в формуле (3), будет совпадать со знаком производной 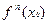 . Поэтому при переходе через точку
. Поэтому при переходе через точку  правая, а значит и левая часть формулы (3) будет менять свой знак тогда, когда меняет свой знак многочлен
правая, а значит и левая часть формулы (3) будет менять свой знак тогда, когда меняет свой знак многочлен 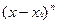 . Очевидно при
. Очевидно при 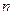 нечетном он вместе с разностью
нечетном он вместе с разностью
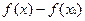 (4) свой знак меняет при переходе через точку
(4) свой знак меняет при переходе через точку  , а при
, а при 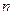 четном он вместе с этой разностью знака не меняет.
четном он вместе с этой разностью знака не меняет.
Теперь заметим, что если разность (4) при переходе через точку  меняет свой знак, то в точке
меняет свой знак, то в точке  , очевидно, нет локального экстремума, т.е. его нет при
, очевидно, нет локального экстремума, т.е. его нет при 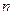 нечетном. Если же она не меняет своего знака при переходе через эту точку, то в ней есть локальный экстремум, т.е. он есть при
нечетном. Если же она не меняет своего знака при переходе через эту точку, то в ней есть локальный экстремум, т.е. он есть при 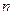 четном.
четном.
Далее, если при переходе через точку  разность (4) остается положительной, то, очевидно, точка
разность (4) остается положительной, то, очевидно, точка  - точка локального минимума функции
- точка локального минимума функции  . А это имеет место при четном
. А это имеет место при четном 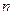 и положительной производной
и положительной производной 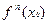 . Наконец, если при переходе через точку
. Наконец, если при переходе через точку  разность (4) остается отрицательной, то, очевидно, точка
разность (4) остается отрицательной, то, очевидно, точка  - точка локального максимума. Последнее условие, в свою очередь, выполнено когда
- точка локального максимума. Последнее условие, в свою очередь, выполнено когда 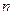 - четное, а
- четное, а 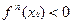 □
□
n°4. Условия выпуклости функции.
Определение 2. Функция 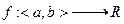
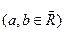 называется выпуклой (соотв., вогнутой) на промежутке
называется выпуклой (соотв., вогнутой) на промежутке 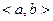 , если для любых
, если для любых 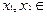
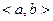 и любых
и любых 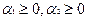 таких, что
таких, что 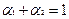 имеет место неравенство:
имеет место неравенство:
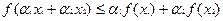 (соотв.,
(соотв., 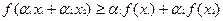 ). ).
| (1) |
При этом, если это неравенство является строгим при 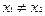 и
и 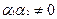 , то функция
, то функция 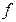 называется строго выпуклой (строго вогнутой).
называется строго выпуклой (строго вогнутой).
Замечание 1. В этом определении без ущерба для общности можно считать, что 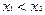 и
и 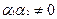 . Эти неравенства далее предполагаются выполненными.
. Эти неравенства далее предполагаются выполненными.
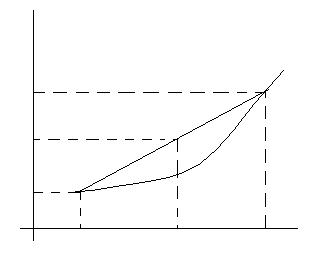 |
Замечание 2. Геометрически условие (1) означает, что любая дуга графика функции лежит под хордой, стягивающей эту дугу (см. рис.1)
Рис.1
Аналогичное условие вогнутости функции означает, соответственно, что любая дуга графика функции лежит над хордой, стягивающей эту дугу.
Замечание 3. Очевидно, фунуция  является вогнутой в том и только том случае, когда функция
является вогнутой в том и только том случае, когда функция 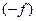 является выпуклой. Поэтому далее мы ограничимся изучением только выпуклых функций, при этом утверждения, устанавливаемые ниже для выпуклых функций, читателю предлагается самостоятельно переформулировать для вогнутых функций.
является выпуклой. Поэтому далее мы ограничимся изучением только выпуклых функций, при этом утверждения, устанавливаемые ниже для выпуклых функций, читателю предлагается самостоятельно переформулировать для вогнутых функций.
Теорема 5. Для того, чтобы дифференцируемая на интервале  функция
функция  была выпуклой (строго выпуклой) на нем необходимо и достаточно, чтобы её производная
была выпуклой (строго выпуклой) на нем необходимо и достаточно, чтобы её производная 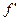 была неубывающей (соответственно, возрастающей) на интервале
была неубывающей (соответственно, возрастающей) на интервале  функцией.
функцией.
Д о к а з а т е л ь с т в о. Пусть 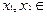
 ,
, 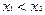 ,
, 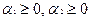 ,
, 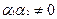 ,
, 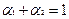 . Положим
. Положим 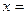
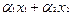 . Тогда нетрудно видеть, что
. Тогда нетрудно видеть, что
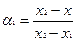 , , 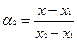
| (2) |
Поэтому неравенство (1) можно переписать в виде
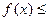
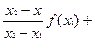
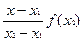 В свою очередь, так как
В свою очередь, так как 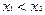 , то последнее неравенство равносильно следующему неравенству:
, то последнее неравенство равносильно следующему неравенству:
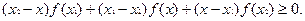 Наконец, так как
Наконец, так как 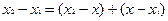 , то из предыдущего следует, что:
, то из предыдущего следует, что:
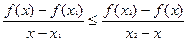
| (3) |
Устремляя здесь сначала 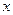 к
к 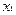 , а затем
, а затем 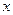 к
к 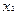 , в итоге получим:
, в итоге получим:
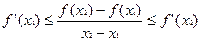 .
.
В силу произвольности точек 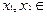
 ,
, 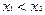 , это неравенство означает, что производная
, это неравенство означает, что производная 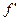 выпуклой функции на интервале
выпуклой функции на интервале  является неубывающей на этом интервале функцией.
является неубывающей на этом интервале функцией.
Пусть теперь функция  - строго выпуклая на интервале
- строго выпуклая на интервале  . Тогда легко заметить, что неравенство (3) будет строгим. Поэтому, с учетом монотонности производной
. Тогда легко заметить, что неравенство (3) будет строгим. Поэтому, с учетом монотонности производной 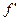 , на основе теоремы Лагранжа получим
, на основе теоремы Лагранжа получим
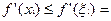
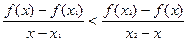
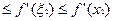 ,
,
где 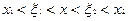 . Таким образом, строгая выпуклость функции
. Таким образом, строгая выпуклость функции  влечет строгую монотонность ее производной
влечет строгую монотонность ее производной 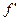 , точнее гарантирует, что она является возрастающей на интервале
, точнее гарантирует, что она является возрастающей на интервале  функцией. Следовательно, необходимость условия теоремы доказана.
функцией. Следовательно, необходимость условия теоремы доказана.
Докажем достаточность. С этой целью заметим, что как следует из вывода неравенства (3) оно при условии (2) равносильно неравенству (1). Поэтому нетрудно видеть, что функция  является выпуклой на интервале
является выпуклой на интервале  тогда и только тогда, когда для любых
тогда и только тогда, когда для любых 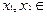
 ,
, 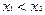 и любого
и любого 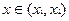 имеет место неравенство (3).
имеет место неравенство (3).
Пусть 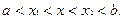 Тогда по теореме Лагранжа:
Тогда по теореме Лагранжа:
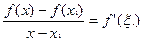 ,
,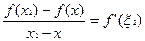 где
где 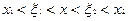 , и если производная
, и если производная 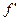 не убывает (возрастает) на интервале
не убывает (возрастает) на интервале  , то
, то 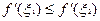 (
(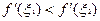 ), а значит, имеет место и неравенство (3), которое в силу произвольности точек
), а значит, имеет место и неравенство (3), которое в силу произвольности точек 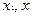 и
и 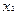 , удовлетворяющих неравенствам
, удовлетворяющих неравенствам 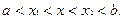 гарантирует выпуклость (строгую выпуклость) функции
гарантирует выпуклость (строгую выпуклость) функции  на
на  □
□
Из теорем 1 и 4 вытекает следующее
Следствие. Для того, чтобы дважды дифференцируемая на интервале  функция была выпуклой на этом интервале необходимо и достаточно, чтобы
функция была выпуклой на этом интервале необходимо и достаточно, чтобы
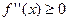
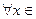
 .
.
Если же
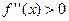
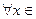
 ,
,
то этого достаточно, чтобы функция  была строго выпуклой на интервале
была строго выпуклой на интервале  .
.
Отметим без доказательства еще один интуитивно ясный, геометрический критерий выпуклости (строгой выпуклости) дифференцируемой функции.
Теорема 6. Дифференцируемая на интервале 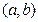 функция является выпуклой на нем тогда и только тогда, когда ее график всеми своими точками лежит не ниже любой проведенной к нему касательной. В свою очередь для строгой выпуклости дифференцируемой на интервале функции необходимо и достаточно, чтобы все точки ее графика лежали выше любой проведенной к нему касательной за исключением самой точки касания.
функция является выпуклой на нем тогда и только тогда, когда ее график всеми своими точками лежит не ниже любой проведенной к нему касательной. В свою очередь для строгой выпуклости дифференцируемой на интервале функции необходимо и достаточно, чтобы все точки ее графика лежали выше любой проведенной к нему касательной за исключением самой точки касания.
В заключение этого параграфа коснемся так называемых точек перегиба графика.
Определение 3. Пусть функция 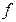 определена и дифференцируема в некоторой окрестности точки
определена и дифференцируема в некоторой окрестности точки 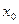 . Если существует такое
. Если существует такое 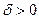 , что на интервале
, что на интервале 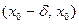 функция
функция 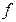 строго выпукла (строго вогнута), а на интервале
строго выпукла (строго вогнута), а на интервале 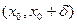 , напротив, строго вогнута (соотв., строго выпукла), то точка
, напротив, строго вогнута (соотв., строго выпукла), то точка 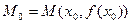 ее графика называется точкой перегиба.
ее графика называется точкой перегиба.
Таким образом, можно сказать, что при переходе через точку перегиба меняется направление выпуклости графика функции, при этом график функции как бы переходит с одной стороны касательной в этой точке на другую ее сторону.
Если точка 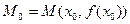 является точкой перегиба графика дважды дифференцируемой в точке
является точкой перегиба графика дважды дифференцируемой в точке 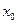 функции
функции 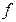 , то в соответствии с определением 3 и теоремой 5 точка
, то в соответствии с определением 3 и теоремой 5 точка 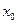 – точка локального экстремума производной
– точка локального экстремума производной 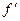 и поэтому по теореме Ферма
и поэтому по теореме Ферма 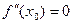 . Это условие, таким образом, является необходимым условием того, чтобы точка
. Это условие, таким образом, является необходимым условием того, чтобы точка 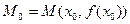 была точкой перегиба графика дважды дифференцируемой функции
была точкой перегиба графика дважды дифференцируемой функции 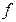 .
.
В свою очередь, в силу определения 3 и теоремы 5, если в некоторой левосторонней проколотой окрестности 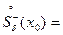
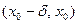 точки
точки 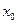 вторая производная
вторая производная 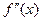 имеет один знак, а в соответствующей правосторонней проколотой окрестности
имеет один знак, а в соответствующей правосторонней проколотой окрестности 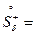
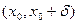 она имеет другой знак, то этого достаточно для того, чтобы точка
она имеет другой знак, то этого достаточно для того, чтобы точка 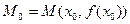 была точкой перегиба.
была точкой перегиба.
Глава 4. Интегральное исчисление функций одной переменной
 2014-02-09
2014-02-09 774
774








