Потенциальная энергия шарика имеет вид

U = kх ²/2. (13.9)

Если такой шарик вывести из состояния равновесия, то он будет совершать гармонические колебания с частотой w = (k / m)^1/2.

Из (13.9) видно, что потенциальная кривая гармонического осциллятора является параболой. Поэтому задача о гармоническом осцилляторе – это задача о поведении частицы в потенциальной яме параболической формы.

Для решения задачи о квантовомеханическом осцилляторе необходимо найти конечное, однозначное, непрерывное и гладкое решение уравнения Шредингера при U = – kх ²/2, т. е. уравнения

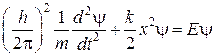. (13.10)

Точное решение уравнения (13.10) приводит к следующему выражению для спектра возможных значений энергии осциллятора:

,

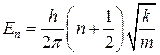где п = 0, 1, 2, ….

Отсюда видно, что наименьшее значение энергии осциллятора не равно нулю. Значение энергии осциллятора при n = 0

называется «нулевой энергией».

Квантовомеханическая частица не может «лежать» на дне параболической потенциальной ямы, точно так же как она не может лежать на дне прямоугольной, или какой бы то ни было другой потенциальной ямы конечной ширины.

Энергия осциллятора пропорциональна первой степени п, поэтому энергетические уровни оказываются равноотстоящими один от другого (эквидистантными).

Чтобы «раскачать» осциллятор, нужно добавить ему энергию, равную разности энергий соседних уровней. Изменение (например, приращение) энергии осциллятора соответствует переходам между уровнями энергии E_n (указаны стрелками).

Рис.13.3

На рис. 13.4, а - графики волновых y-функций, являющихся решениями уравнения (13.10) при п = 0, 1, 2 и 6; вдоль оси х отложены отрезки, равные удвоенным амплитудам колебаний классического осциллятора при Е, равных E_n .

На рис. 13.4, б сплошными кривыми изображены кривые распределения плотности вероятности |y(x)| ² для тех же состояний квантового осциллятора, а пунктиром – плотность вероятности найти классический осциллятор в окрестности точки х.

а

б

Рис. 13.4

Видно, что при малых квантовых числах п квантовомеханический осциллятор ведет себя совершенно иначе, чем классический. Вероятность найти классический осциллятор всегда является наибольшей для точек поворота, так как в этих точках его скорость равна нулю, а для квантовомеханического осциллятора вероятность оказывается максимальной в точках, соответствующих «пучностям» y-функции.

Но при больших п усредненная кривая для распределения плотности вероятности квантовомеханического осциллятора хорошо согласуется с кривой для классического осциллятора.

Следует отметить еще одну особенность квантовомеханического осциллятора:

квадрат функции |y(x)|² не равен нулю за точками поворота (т. е. вне пределов, ограничивающих движение классического осциллятора).