Принцип Даламбера

Пусть материальная точка движется под действием силы F, и ее движение ограничено какой-то связью с реакцией R. Тогда по второму закону Ньютона можно записать

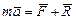. (93)

Перепишем (93) в виде

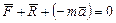. (94)

Введем обозначение 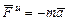- даламберова сила инерции и запишем (94) с учетом обозначения

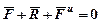. (95)

Уравнение (95) выражает следующий принцип Даламбера для материальной точки:

Если в каждый момент времени к действующим на материальную точку активным силам и реакциям связей добавить силу инерции, то полученная система сил будет подчиняться всем законам статики.

Если материальная точка входит в систему, то нее уравнение (95) приобретает вид

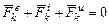, (96)

где 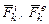- соответственно равнодействующие внутренних и внешних сил, действующих на точку.

Если уравнение (96) записать для всех точек системы, то можно сформулировать принцип Даламбера и для всей системы в целом.

Как известно из статики, для равновесия произвольной системы сил необходимо и достаточно, чтобы геометрическая сумма всех сил и геометрическая сумма моментов этих сил относительно любой точки равнялись нулю. Следовательно, принцип Даламбера для системы может быть записан в виде двух условий

,

.

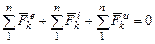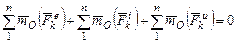Введем обозначения 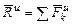- главный вектор сил инерции, 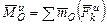- главный момент от сил инерции.

С учетом обозначений получим

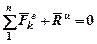, (97)

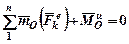. (98)

Уравнения (97) и (98) выражают принцип Даламбера для системы:

Если к действующим на систему силам добавить главный вектор сил инерции, а к моментам сил добавить главный момент от сил инерции относительно одной и той же точки, то для полученной системы сил и моментов будут справедливы условия равновесия, и все методы статики.

При всех видах движения системы главный вектор сил инерции по величине и направлению определяется как произведение массы системы на ускорение центра масс, взятое с обратным знаком

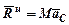. (99)

Методика определения главного момента от сил тнерции зависит от вида движения системы:

1. Поступательное движение

Так как в этом случае тело не совершает вращательного движения, то сумма моментов всех внешних сил системы относительно любой точки равна нулю, следовательно, главный момент равен нулю.

2. Вращательное движение

Пусть тело совершает вращение относительно неподвижной оси z, тогда на основе теоремы об изменении кинетического момента для него будет справедливо уравнение (92). Решая его совместно с (98), получим

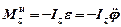. (100)

При вращательном движении главный момент сил инерции относительно оси вращения равен произведению момента инерции тела относительно оси вращения на угловую скорость, взятое с обратным знаком.

Если w=const, то .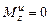

3. Плоское движение

Если при изучении плоского движения в качестве полюса выбрать центр масс, то движение можно рассматривать как поступательное движение вместе с центром масс и вращательное относительно центра масс. В этом случае главный вектор сил инерции определяется по уравнению (99), а для определения главного момента от сил инерции можно записать

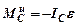. (101)