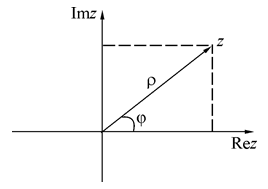
 Рассмотрим комплексное число
Рассмотрим комплексное число  , заданное в алгебраической форме. Перейдем от декартовой системы координат к полярной:
, заданное в алгебраической форме. Перейдем от декартовой системы координат к полярной:
 ,
, 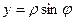 .
.
Тогдаполучим: 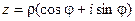 .
.
Полученная запись называется тригонометрической
формой записи комплексного числа.
При этом величина 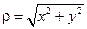 называется модулем комплексного числа и задает расстояние от точки z до начала координат. Величина
называется модулем комплексного числа и задает расстояние от точки z до начала координат. Величина  задает угол между положительным направлением оси абсцисс и радиусом - вектором направленным в точку z. Эта величина называется аргументом комплексного числа, обозначается
задает угол между положительным направлением оси абсцисс и радиусом - вектором направленным в точку z. Эта величина называется аргументом комплексного числа, обозначается 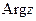 и находится неоднозначно а с точностью до величины кратной
и находится неоднозначно а с точностью до величины кратной 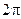 .
. 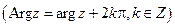 . Здесь
. Здесь 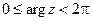 и называется главным значением аргумента комплексного числа (иногда главным значением аргумента комплексного числа называется угол, удовлетворяющий условию
и называется главным значением аргумента комплексного числа (иногда главным значением аргумента комплексного числа называется угол, удовлетворяющий условию 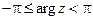 ). Какое из этих значений считается главным должно быть ясно из контекста.
). Какое из этих значений считается главным должно быть ясно из контекста.
F0. Два комплексных числа, заданные в тригонометрической форме равны тогда и только
тогда когда их модули совпадают, а аргументы либо совпадают, либо отличаются на
величину кратную 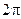 .
.
|
|
|
Для комплексного числа z = 0 аргумент не определен (его можно считать равным чему угодно).
Пусть 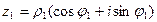 ,
, 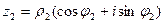 два комплексных числа, заданных в тригонометрической форме. Тогда непосредственным умножением легко проверить, что:
два комплексных числа, заданных в тригонометрической форме. Тогда непосредственным умножением легко проверить, что:
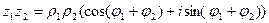 ,
, 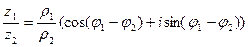 т.е.
т.е.
при умножении комплексных чисел модули чисел умножаются, а аргументы складыва- ются, а при делении комплексных чисел их модули делятся, а аргументы вычитаются.
Тогда формула 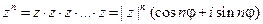 задает правило возведения комплексного числа в натуральную степень.
задает правило возведения комплексного числа в натуральную степень.
Кроме того, получена весьма важная формула, которая называется формулой Муавра:
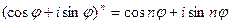 .
.
 2014-02-24
2014-02-24 609
609








