1. По определению 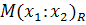 тогда и только тогда, когда
тогда и только тогда, когда 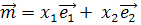 , где
, где 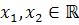 (действительные числа),
(действительные числа), 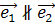 .
.
2. Так как вектор 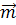 , порождающий точку
, порождающий точку 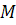 проективной прямой, ненулевой (
проективной прямой, ненулевой (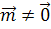 ), то хотя бы одна из его координат отличная от нуля.
), то хотя бы одна из его координат отличная от нуля.
3. Точка 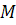 может порождаться бесконечным множеством векторов, любые два из них коллинеарны и, следовательно, имеют пропорциональные координаты.
может порождаться бесконечным множеством векторов, любые два из них коллинеарны и, следовательно, имеют пропорциональные координаты.
Поэтому точка имеет в данной системе координат бесконечное множество пар координат.
Соответствующие координаты любой из этих пар пропорциональны, и их отношение 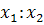 определено однозначно.
определено однозначно.
Обозначение: 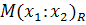 .
.
Пример 1. На расширенной евклидовой прямой 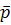 выбран проективные репер R, состоящий из собственных точек
выбран проективные репер R, состоящий из собственных точек 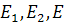 . Построить точку
. Построить точку 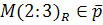 .
.
Решение:
1. 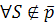 .
.
2. 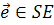 .
.
3.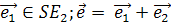 (на прямых
(на прямых 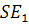 и
и 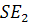 как сторонах параллелограмма с диагональю
как сторонах параллелограмма с диагональю 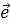 ).
).
4. 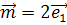 +3
+3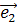 .
.
5. 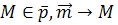 (точка
(точка 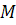 порождается вектором
порождается вектором 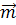 ).
).

Так как точка 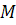 порождается кроме вектора
порождается кроме вектора 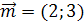 и любым ему коллинеарным вектором, например, вектором
и любым ему коллинеарным вектором, например, вектором 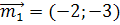 , то координаты всех таких векторов пропорциональны:
, то координаты всех таких векторов пропорциональны: 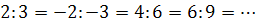
Числа любой из этих пар можно считать проективными координатами точки 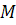 на проективной прямой.
на проективной прямой.
Для того, чтобы подчеркнуть важность не самих проективных координат, а их отношений, пишут 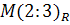 , а не
, а не 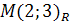 .
.
Пример 2. 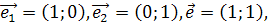 поэтому
поэтому
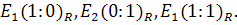
Имеет место важная теорема.
Теорема. Проективные координаты (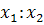 ) произвольной точки
) произвольной точки 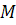 проективной прямой в репере
проективной прямой в репере 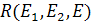 выражаются через её «новые» координаты (
выражаются через её «новые» координаты (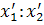 ) в репере
) в репере 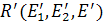 формулами:
формулами:
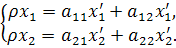
| (1) |
где 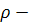 произвольный ненулевой множитель и
произвольный ненулевой множитель и
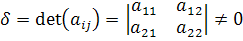
| (2) |
Доказательство:
Пусть точки 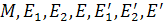 порождаются соответственно векторами
порождаются соответственно векторами 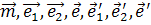 . Тогда (
. Тогда (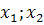 ) – координаты вектора
) – координаты вектора 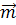 в базисе (
в базисе (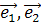 ), а (
), а (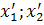 ) – координаты того же вектора в базисе (
) – координаты того же вектора в базисе (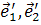 ). Следовательно, их связывают формулы перехода от одного базиса к другому. Эти формулы имеют вид (1) при
). Следовательно, их связывают формулы перехода от одного базиса к другому. Эти формулы имеют вид (1) при 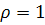 и условии (2).
и условии (2).
Так как проективные координаты точки на проективной прямой определены с точностью до произвольного общего множителя (отличного от нуля), то в левой части формул (1) появляется множитель 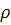 .
.
Теорема доказана.
 2014-02-24
2014-02-24 1090
1090








