Формы показателя эффективности

Показатель эффективности в форме (1.4) является, наиболее общим. В за­висимости от вида оценочной функции 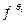и функции соответствия ρ(Y (u), Y^TP) из (2.3) можно получить различ­ные показатели эффективности.

Покажем это на примере «объектив­ных» скалярных показателей, часто используемых при исследованиях эф­фективности технических систем.

С целью отличия случайной величины от ее возможного значения, когда это не ясно из контекста, над соответствую­щей буквой будем ставить символ Д. Например, 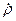— случайная величина, ρ — ее возможное значение.

Пусть цель операции описывается случайным событием А, наступление которого является желательным ре­зультатом операции. Комплекс усло­вий, а следовательно, и вероятность Р_u (А) наступления этого события зависят от стратегии u 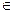U. Функцию соответствия ρ в этом случае вводят как бернуллиеву переменную, которая может принять лишь два значения: 0 или 1, то есть 1, если событие А наступило; ρ(y(u), y^TP) = 0 в противном случае.

Очевидно, при таком введении функ­ции соответствия y^TP=1. Вероятность события А есть математическое ожи­дание бернуллиевой переменной, или функции соответствия (1.6).

Действительно,

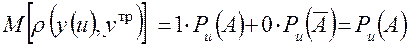
и, следовательно, показатель эффек­тивности в форме (1.3) есть вероятность наступления события А:

.

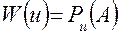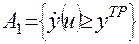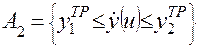Часто событие А выражается отно­шением между реальным результатом у (u) и требуемым y^TP. Например, или . Функ-ции соответствия для этих событий вводятся следующим образом:

для события A₁

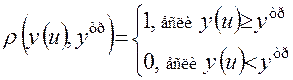, (1.7)

для события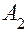

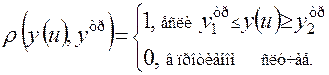
Функцию соответствии (1.7) употреб­ляют в случаях, когда требуемый ре­зультат задачи и его достижение яв­ляются непременным условием выпол­нения поставленной задачи. При этом показатель эффективности

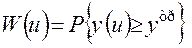(1.8)

трактуется как вероятностная гаран­тия (или степень гарантии) выполне­ния поставленной задачи. Например, если цель операции заключается в обес­печении повышения срока службы изделия до уровня не ниже требуемого i/TP, то показатель эффективности опе­рации (1.8) есть степень гарантии или вероятность того, что срок службы изделия будет не менее требуемого. При известной функции распределения реального результата Fu (у) (1.8) записывают в следующем виде: .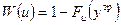

На рис. 1.6 изображена функция распределения результата операции и показана вероятностная гарантия (вероятность Р {у (u) > у^TP}).

Допустим, что имеет место некоторая неопределенность при установлении требуемого результата операций у^TP. Если эта неопределенность нестохастического характера, то можно ввести функцию принадлежности µ_А(у) для нечеткого случайного события 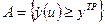. В записи события А временная y(ω) является случайной величиной с функцией распределения F_u (у), но У^тр есть неопределенная (временная нестохастического характера с функцией принадлежности µ_А(у)).

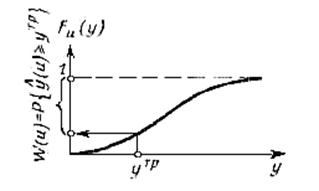
Рис. 1.6. Функция распределения результата операции. Вероятностная гарантия

Нечеткое случайное событие А введем следующим образом. Как известно из теории вероятностей, случайное событие А есть подмножество пространства элементарных событий Е, то есть A 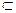E. Предположим теперь, что А есть нечеткое подмножество Е (то есть А 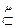Е), заданное функцией принад­лежности µ_А (для простоты будем пока рассматривать случай, когда Е не более чем счетно). Теперь каждому элементарному событию е_i 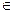Е следует по­дставить в соответствие не только веро­ятность его наступления Р(е_i), но и степень принадлежности е_i подмножеcтву А, то есть µ_А(е_i), (0<µ_А (е_i)< 1). Чтобы найти вероятность наступления нечеткого случайного события А, сле­дует по всем e_i 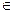Е просуммировать произведения µ_А(е_i) Р (е_i), то есть

.

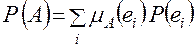Эта запись есть математическое ожи­дание дискретной случайной величины µ_А. Таким образом, вероятность на­ступления нечеткого случайного собы­тия есть математическое ожидание функции принадлежности этого не­четкого события, то есть

. (1.9)

Если целью операции является до­стижение результата у (u) не ниже требуемого уровня при нечетком зада­нии последнего, то функцию соответ­ствия можно ввести по аналогии с (1.7):

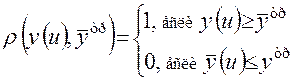(1.10)

и тогда

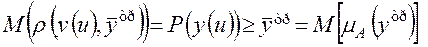
или в общем виде

.

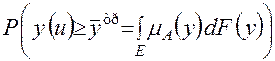Однако в качестве функции соответ­ствия в этих условиях может быть использована и сама функция принад­лежности, то есть

.

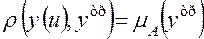Она в определенном смысле эквива­лентна (1.7).

В практике оценки эффективности операций приходится иногда учиты­вать случайный характер требуемого результата. Например, в качестве ре­зультата операции по повышению на­дежности технической системы можно потребовать, чтобы срок ее безаварий­ной работы был не менее периода вре­мени активных работ с использованием этой системы.

Здесь срок безаварийной работы и период времени активных работ могут иметь случайный характер, то есть тре­буемый результат в этих условиях описывается случайной переменной y^ТР, которую обычно называют минимально необходимым результатом. Если y^ТР — случайная величина (числовая случай­ная переменная), то ее распределение вводят обычно с помощью функции распределения F_H (у).

В случаях, когда целью операции является достижение результата y (u)

не ниже требуемого уровня y^тр при случайном характере последнего, функ­цию соответствия можно ввести по аналогии с (2.6):

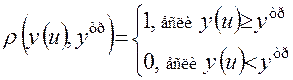. (1.11)

Показатель эффективности

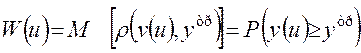
в рассматриваемых условиях представ­ляет собой математическое ожидание функции соответствия (2.10) и является вероятностной гарантией того, что реальный результат будет не менее требуемого при случайном характере как реального, так и требуемого ре­зультатов.

Функция распределения F_H (у) необ­ходимого результата представляет со­бой условную вероятность события {y^тр < у}, вычисленную в предполо­жении, что реальный результат принял значение у (то есть наступило событие {у < y < y + dy}).

Таким образом,

,

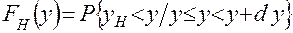но, очевидно,

,

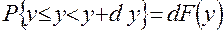где 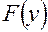— функция распределения реального результата. Используя формулу полной вероятности, получим

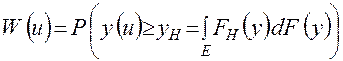. (1.12)

Здесь интегрирование проводится по всему пространству элементарных со­бытий Е, на котором определены слу­чайные величины y и y_н.

При исследовании эффективности операций широко распространен по­казатель среднего результата, то есть

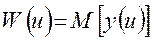. (1.13)

Этот показатель используется в тех случаях, когда цель операции выра­жается числовой переменной. Очевидно, что (1.13) является частным случаем показателя (2.2), при котором функция соответствия равна реальному результату

.

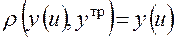Вводя показатель среднего резуль­тата и зная, например, диапазон изме­нения результата, исследователь может сравнить его значение с предельно большим значением.

Важным свойством показателя сред­него результата является его аддитивность, то есть

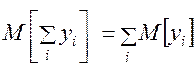. (1.14)

Если результат операции у(и) пред­ставим в виде суммы результатов дей­ствий подсистем 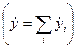, то средний результат операции равен сумме средних частных результатов, несмотря на возможную их стохастическую за­висимость.

Если цель операции носит количе­ственный характер, то в качестве по­казателя эффективности операции на­ряду с (1.8) может быть принят мини­мальный результат у_α, получаемый с заданной вероятностью α, то есть

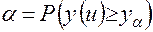. (1.15)

Очевидно,

,

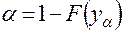где 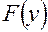— функция распределения реального результата операции (случайной величины .

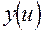Решив это уравнение относительно 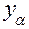, получим

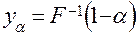. (1.16)

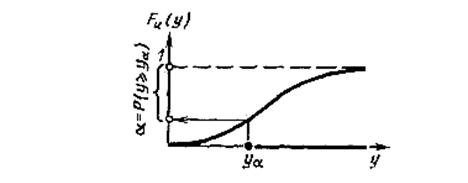
Рис. 1.7. Функция распределения результата операции. Гарантированный результат

Здесь 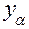есть обратная функция к функции распределения 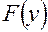при значении аргумента (1 — α) (квантиль распределения 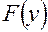). На рис. 1.7 изобра­жена функция распределения резуль­тата операции и показан гарантирован­ный результат (переход от (1 — α) к ).

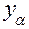При этом функция соответствия

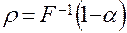(1.17)

есть величина неслучайная и ее математическое ожидание, следовательно, равно .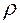

Таким образом, показатель эффективности в форме (2.2) имеет вид

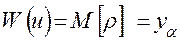. (1.18)

Этот показатель обычно называют ве­роятностно-гарантированным резуль­татом. Требуемый результат косвенно отражает заданный (требуемый) уро­вень вероятности а (степень гарантии).

Иногда в качестве показателя эффек­тивности в условиях, когда результат описывается случайной величиной, при­ходится использовать характеристику рассеяния (кучности) реального ре­зультата относительно требуемого зна­чения или относительно своего мате­матического ожидания. Функции соот­ветствия в этом случае имеют вид

;

.

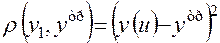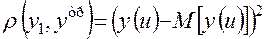В первом случае показатель эффек­тивности есть математическое ожида­ние квадрата уклонения реального результата от требуемого:

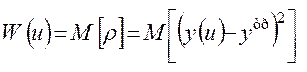, (1.19)

а во втором случае – дисперсия реального результата:

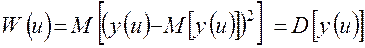. (1.20)

В практике исследований эффектив­ности технических систем показатели (1.19) и (2Л 9) обычно используют как вспомогательные.

В качестве показателя эффективности операций, связанных, например, с рас­познаванием некоторых ситуаций, об­разов, объектов и т. п., теория стати­стических решений рекомендует вы­бирать средние потери (средний риск), которые появляются при неправильном (ошибочном) распознавании.

В этих задачах в качестве функции соответствия принимаются потери П_ij, связанные с тем, что объект, принадле­жащий множеству H_i, был ошибочно (при i ≠ j) отнесен к множеству H_j. Здесь, следовательно, функция соот­ветствия имеет вид

.

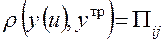Пусть Р (H_i) — вероятность того, что объект принадлежит множеству H_i; Р_u(H_j/H_i) — условная вероят­ность отнесения объекта из множества H_i к множеству H_j (вероятность ошибки при i ≠ j)

Показатель эффективности операции по распознаванию объекта записы­вается в виде средних потерь (байесов­ский средний риск):

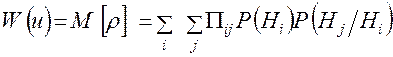. (1.21)

И в этом случае показатель эффек­тивности имеет форму (2.2), то есть яв­ляется математическим ожиданием функции соответствия ρ = П_ij.

Индекс u в записи условной вероят­ности Р_u (H_j/H_i) показывает, что она зависит от стратегии распознавания 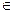u U.

Рассмотрим один из способов введе­ния показателя эффективности для случая конфликтных ситуаций при наличии неопределенности в поведе­нии оппонента. Пусть имеет место конфликтная ситуация, и на результат операции влияет не только выбор стратегии u 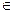U лицом, принимаю­щим решение, но и выбор стратегии v оппонентом из известного множества его допустимых стратегий V. Таким образом, результат операции у (u, v) зависит от 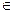u U и u 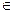V. Функция соответствия, как и в предыдущих примерах, будет измерять степень соот­ветствия реального результата опера­ции требуемому:

.

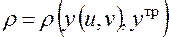При наличии случайных факторов введем математическое ожидание функ­ции соответствия (условный показатель эффективности):

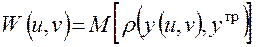(1.22)

и выдвинем гипотезу поведения оппо­нента: он выбирает свои стратегии v £ V так, чтобы при любой стратегии ЛПР u 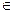U минимизировать степень соответствия реального результата опе­рации желаемому для ЛПР (то есть ин­тересы оппонента противоположны ин­тересам ЛПР). В этих условиях в ка­честве показателя эффективности для ЛПР можно выбрать минимальное зна­чение W (u, v) для каждой стратегии u 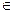U, то есть

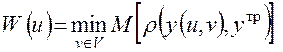. (1.23)

Эта форма показателя эффективности операции уже отличается несколько от (2.2). Однако функция соответствия р (у (u, v), у^TP) в выражении (1.23) может принимать любой вид из тех, которые были рассмотрены в преды­дущих примерах. Смысл показателя W (u) заключается в том, что он яв­ляется гарантированным уровнем ус­ловного показателя W (u, v). При любой стратегии оппонента и фикси­рованной стратегии ЛПР W (u) ≤W(u,v),то есть W (u) является нижней границей среднего значения функции соответствия реального результата опе­рации требуемому (для ЛПР).

Вопросы для самопроверки по разделу 1

1. Что называется системой?

2. Что такое эмерджентность?

3. Какие системы относятся к сложным?

4. В чем отличие сложных систем от простых?

5. Что обусловило привлечение методологических средств системного анализа для решения крупных научно-технических проблем?

6. Какие моменты включает понятие операция?

7. Дайте определение цели?

8. Что такое управляемая подсистема?

9. Что называется состоянием системы?

10. Что называется эффективностью операции?

11. Что понимается под потенциальной эффективностью?

12. Что понимается под фактором?

13. Какие факторы, определяющие эффективность операций в технике, вы знаете?

14. Какие качества сложной системы вы знаете?

15. Какие показатели эффективности вы знаете?

16. Какие критерии эффективности вы знаете?