Схема исследования функции элементарными способами.
График функции. Способы задания функций.
Пусть задана функция f с областью определения D. Рассмотрим координатную плоскость. По оси абсцисс откладываем значения аргумента, а по оси ординат значения функции. Для каждого числа x 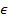 D можно вычислить y=f(x) и построить точку М(x; f(x)). Множество всех таких точек образует кривую, называемую графиком функции f в заданной системе координат.
D можно вычислить y=f(x) и построить точку М(x; f(x)). Множество всех таких точек образует кривую, называемую графиком функции f в заданной системе координат.
♯ Графиком функции f называется множество точек плоскости с координатами (x; f(x)), где х пробегает область определения функции f.
Способы задания функции:
1) Запись функциональной зависимости в виде формулы (функция задана аналитическим выражением). Пример: S= π R2
Область допустимых значений аналитического выражения π R2 – все значения R; область определения функции, определенной данным выражением, есть 0<R<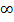 .
.
Если функция задана аналитическим выражением относительно аргумента x и область определения не указана, то подразумевают, что область определения совпадает с ОДЗ задающего ее выражения.
|
|
|
2) Табличный способ – для избранных значений аргумента x, обычно отстоящих друг от друга на некоторую постоянную величину – шаг таблицы, указываются соответствующие значения y (с определенной степенью точности).
3) Графический способ
Основные определения:
1) Функция f(x), область определения которой симметрична относительно начала отсчета О, называется четной, если для 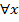 из ее области определения выполняется равенство f(-x)= f(x).
из ее области определения выполняется равенство f(-x)= f(x).
График четной функции симметричен относительно оси Оу. Обратное также верно.
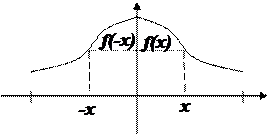
2) Функция f(x), область определения которой симметрична относительно начала отсчета О, называется ytчетной, если для 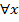 из ее области определения выполняется равенство f(-x)=- f(x).
из ее области определения выполняется равенство f(-x)=- f(x).
График нечетной функции симметричен относительно начала координат. Обратное также верно.
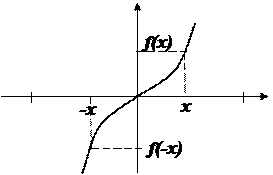
3) Нулем (корнем) функции f(x) называется такое значение аргументах, при котором функция обращается в нуль. Графически нули функции – это точки пересечения графика с осью Ох.
4) Функция называется возрастающей в некотором промежутке, лежащем в ее области определения, если для любых двух значений х1, х2 из этого промежутка из неравенства х1< х2 следует f(х1)< f(х2) (большим значениям аргумента соответствуют большие значения функции). Если из неравенства х1< х2 следует лишь f(х1) 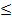 f(х2), то функция называется неубывающей.
f(х2), то функция называется неубывающей.
5) Функция называется убывающей в некотором промежутке, лежащем в ее области определения, если для любых двух значений х1, х2 из этого промежутка из неравенства х1< х2 следует f(х1)> f(х2) (большим значениям аргумента соответствуют меньшее значения функции). Если из неравенства х1< х2 следует лишь f(х1) 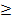 f(х2), то функция называется невозрастающей.
f(х2), то функция называется невозрастающей.
|
|
|
Пример:
|
|
|
y=|x|+x; y= 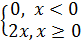
1)
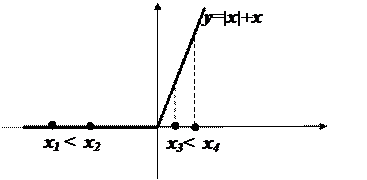 |
х1< х2 2) х1< х2
f(х1)=f(х2) f(х1)< f(х2)
Итак, функция y=|x|+x неубывающая на всей числовой оси.
6)
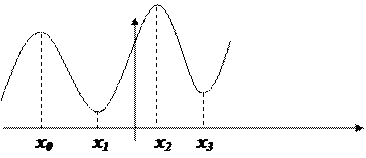 |
Точка х0 называется точкой максимума (минимума) функции y= f(x), если функция определена в самой этой точке и в некоторой окрестности точки x0 выполняется неравенство: f(х0)
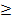 f(х) (для максимума) f(х0)
f(х) (для максимума) f(х0) 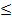 f(х) (для минимума).
f(х) (для минимума).
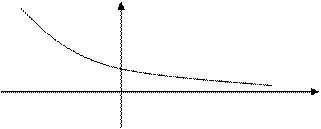
x0, x2 – точки максимума, x1, x3 –точки минимума.
Точки максимума, минимума – точки экстремума.
Максимум функции – ее наибольшее значение по сравнению с «соседними» точками слева и справа, но не обязательно с отдаленными точками.
7)
 |
|
Схема
1. Область определения.
2. Нули функции.
3. Промежутки знакопостоянства.
4. Четность, нечетность функции.
5. Промежутки монотонности.
6. Точки экстремума, точки максимума и минимума функции.
7. Асимптоты.
Пример: 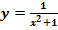
1. D(f)= R
2. f(х)=0
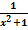 =0 корней нет, следовательно график функции не пересекает ось Ox.
=0 корней нет, следовательно график функции не пересекает ось Ox.
3. 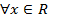 f(х)>0, следовательно график расположен вышеоси Ox.
f(х)>0, следовательно график расположен вышеоси Ox.
4. f(-х)= 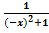 = f(x), следовательно функция четная, график расположен выше оси Oy
= f(x), следовательно функция четная, график расположен выше оси Oy
5. а) х 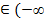 ;0). х1< х2 f(х1)=
;0). х1< х2 f(х1)= 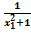 , f(х2)=
, f(х2)= 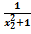 ,
, 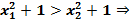 f(х1)< f(х2)⇒ при х
f(х1)< f(х2)⇒ при х 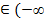 ;0) функция возрастает;
;0) функция возрастает;
б) х 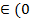 ;
;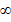 ). х3< х4 f(х3)=
). х3< х4 f(х3)= 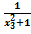 , f(х4)=
, f(х4)= 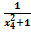 ,
, 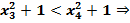 f(х3)> f(х4)⇒ при х
f(х3)> f(х4)⇒ при х 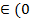 ;
;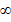 ). функция убывает;
). функция убывает;
6. х=0 – точка максимума (возрастание сменяется убыванием)
у(0)=1 – точка максимума функции.
7. Пусть х→ + 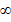 у→ 0
у→ 0
Пусть х→ – 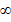 у→ 0
у→ 0
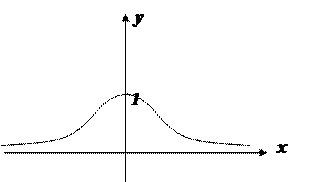 |
Пусть u= 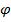 (x) – некоторая функция. Рассмотрим функцию y=f(u), такую, что её область определения совпадала или хотя бы имела общую часть с областью значений функции u=
(x) – некоторая функция. Рассмотрим функцию y=f(u), такую, что её область определения совпадала или хотя бы имела общую часть с областью значений функции u= 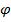 (x). Тогда можно рассматривать y=f(u)= y=f(
(x). Тогда можно рассматривать y=f(u)= y=f( 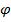 (x)) как функцию от х. Заданная таким образом функция называется сложной функцией. Для вычисления значений сложной функции надо строго соблюдать последовательность производимых операций, т.е. необходимо представить сложную функцию как композицию более простых.
(x)) как функцию от х. Заданная таким образом функция называется сложной функцией. Для вычисления значений сложной функции надо строго соблюдать последовательность производимых операций, т.е. необходимо представить сложную функцию как композицию более простых.
Для записи композиций функций употребляется значок ○. Например, запись h= f○g означает, что функция h получена как композиция функций f и g: сначала применяется g, а затем f, то есть f○g= f(g(х)).
Пример:
f(x)= x2, g(x)= 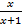 .
.
y= f(g(x))= f○g(x)= 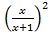
y=g(f(x))= g○ f(x)= 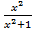 .
.
Из примера видно, что операция образования сложной функции (или композиции функций) не обладает переместительным свойством: f ○ g ≠ g ○ f.
 2014-02-24
2014-02-24 978
978








